第四节 R软件的应用 

一、二项分布

在R中，二项分布是函数dbinom。在R中，所有可能性分布（或连续随机变量情况下的密度）使用字母d作为函数中的第一个字母，然后是部分或整个名称分配给函数名称的其余部分。dbinom作为参数dbinom（x，size，prob），其中x=要使用的k值的向量，size是实验的总数（n），prob是每个实验的成功概率。

在R中使用一些简单的命令来生成概率值，10个蓝眼睛的孩子的概率，服从二项式分布，p=0.16。

>x<-0:10

>y<-dbinom(0:10,10,0.16)

>data.frame("Prob"=y,row.names=x)

结果：

Prob

01.749012e-01

13.331452e-01

22.855530e-01

31.450428e-01

44.834760e-02

51.105088e-02

61.754108e-03

71.909233e-04

81.363738e-05

95.772436e-07

101.099512e-08

因此，给定p = 0.16，10个蓝眼睛孩子中0的概率为0.175；一个蓝眼睛孩子的概率是0.333等等。

当然，如上所述写出概率表只适用于简单的情况，情景并且在大多数情况下是概率分布的图形模型。为了得到与上面相同分布的R中的图形，只需使用plot命令并将二项函数调用做图即可，函数调用如下： 

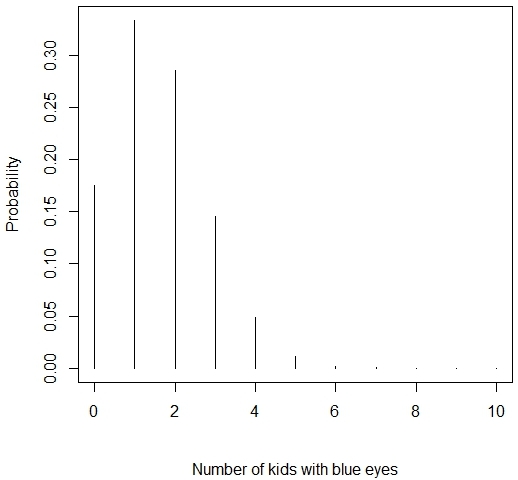
图4-3二项分布的例子，p = 0.16

>plot(0:10,dbinom(0:10,10,0.16),,type='h',xlab="",ylab="Probability",

sub="Numberof kids with blue eyes")

对于这个例子图4-3显示了概率分布函数的图形。 

请注意，这种分布相对于较小的随机值是相当偏斜的变量（X =蓝眼睛的孩子的数量），因为p的值是0.16。考虑到不同的p值图似乎是合理的。如果p的值改变，图形如何改变？

让我们以一个孩子有蓝眼睛的概率重新运行这个例子为0.05，0.2，0.5和0.8，看看这是如何改变分布的。

> par(mfrow=c(2,2))

>plot(0:10,dbinom(0:10,10,0.05),type='h',xlab="",ylab="Prob",sub="p=0.05")

>plot(0:10,dbinom(0:10,10,0.2),type='h',xlab="",ylab="Prob",sub="p=0.2") 

>plot(0:10,dbinom(0:10,10,0.5),type='h',xlab="",ylab="Prob",sub="p=0.5")

>plot(0:10,dbinom(0:10,10,0.8),type='h',xlab="",ylab="Prob",sub="p=0.8") 

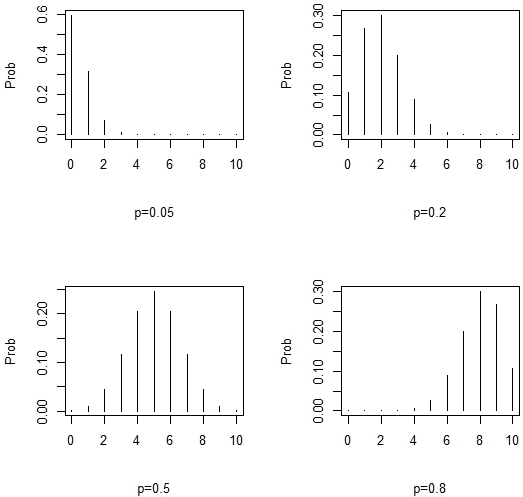
图4-4在二项分布改变p值的效果

请注意图4-4中随机变量的值更大的p如何将分布向更高的方向移动。这应该是有道理的，因为更高的p使孩子更有可能有蓝眼睛，因此10个孩子更多的孩子将会有蓝色的眼睛，如图形模型的转变所代表的那样。还要注意，对于p= 0.5，分布是对称的。这总是对于p = 0.5的二项分布的情况，因为它成功的可能性相同或发生失效。到目前为止，我们只考虑了概率分布函数二项式，累积分布函数如何？回想一下这个是模拟总概率达到并包括某个特定概率的函数随机变量X = x的值。

                

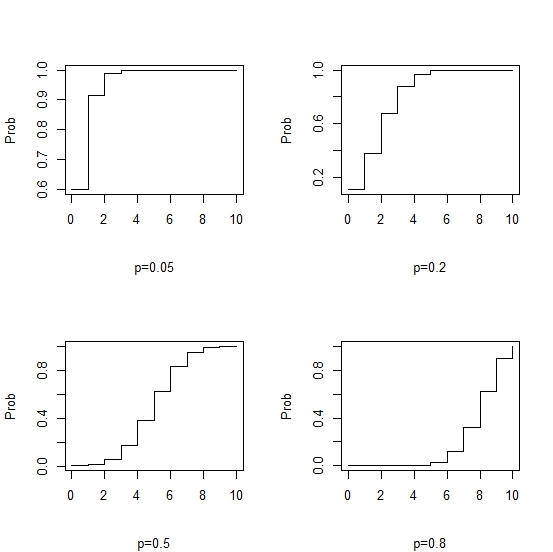
图4-5 使用不同p值的二项式CDF

这在R中使用pbinom分布函数很容易实现，与dbinom相同的参数。实际上，我们可以使用与上面相同的代码获取上例中二项式的CDF图，只将图的类型更改为“s”，并将使用的函数从dbinom更改为pbinom：

> par(mfrow=c(2,2))

>plot(0:10,pbinom(0:10,10,0.05),type='s',xlab="",ylab="Prob",sub="p=0.05")

>plot(0:10,pbinom(0:10,10,0.2),type='s',xlab="",ylab="Prob",sub="p=0.2")

>plot(0:10,pbinom(0:10,10,0.5),type='s',xlab="",ylab="Prob",sub="p=0.5")

> plot(0:10,pbinom(0:10,10,0.8),type='s',xlab="",ylab="Prob",sub="p=0.8") 

使用不同的方法产生二项式的累积概率模式，图4-5显示了p的值。当p很小时（如0.05）累积概率快速达到1，而大的p值导致累积概率不会达到1。如果你只需要对R中的一个值进行简单的计算，你所需要做的就是输入相应的函数和相关的参数值。例如，假设你想知道（正好）10个孩子中有4个孩子蓝眼睛的概率，当p = 0.5时。简单地在R中使用dbinom函数为你计算这个值，如下：

> dbinom(4,10,0.5)

[1] 0.2050781

二、泊松分布

正如我们对二项式做的那样，首先让我们生成一个简单的概率表，X = x表示此分布的值。在这种情况下，理论上X可以从0（无核酸序列错误）到任何长度2000（每bp错误）。但是，已经知道lambda是0.2（也是平均值或期望的错误数量），序列错误的数量不可能超过10，所以下面的代码用于生成表格：

> x<-0:10

> y<-dpois(0:10,0.2)

> data.frame("Prob"=y,row.names=x)

结果：

Prob

0 8.187308e-01

1 1.637462e-01

2 1.637462e-02

3 1.091641e-03

4 5.458205e-05

5 2.183282e-06

6 7.277607e-08

7 2.079316e-09

8 5.198290e-11

9 1.155176e-12

10 2.310351e-14

没有错误（X = 0）的概率是0.818，为1错误（X = 1）的概率是0.163，等等，以2000个碱基对的顺序排列。正如所料，即使值低至10实际上可能性为0。这可以用图形方式查看结果，如图4-6所示。

>plot(0:10, dpois(0:10,0.2), type='h',xlab="Sequence Errors",  ylab="Probability" )   

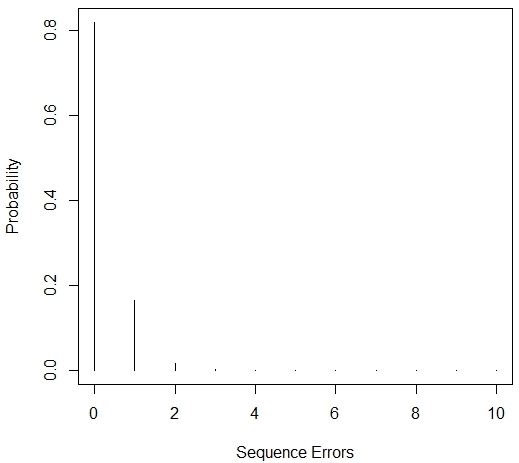
图4-6 泊松分布，λ= 0.2 

在这种情况下，累积分布可能会更有趣一些。因为泊松分布的CDF使用与dpois函数相同参数的ppois函数调用，如上所述。

>plot(0:10,ppois(0:10,0.2),xlab="#Seq Errors", ylab="Cum Prob", type='s') 

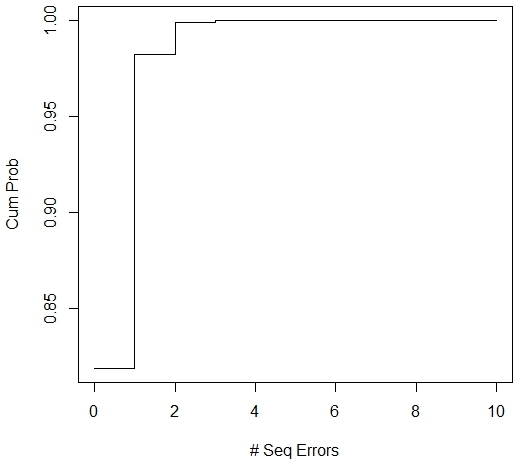
 图4-7 Lambda = 0.2的序列误差Poisson模型的CDF

从图4-7中的CDF图中可以清楚地看出，序列错误的数量在2000个碱基对序列中使用这种方法是不太可能比3大。这个过程不会产生很多错误（除非您正在寻找更严格的可靠性）。R以下用于查找1或更小，2或更小以及3或更小的概率在这个例子中的错误。

> ppois(1,0.2)

[1] 0.982477

> ppois(2,0.2)

[1] 0.9988515

> ppois(3,0.2)

[1] 0.9999432

当参数改变时，泊松概率分布会发生什么改变？为了研究这一点，我们来看几个具有不同lambda值的例子。

> par(mfrow=c(2,2))

>plot(0:10,dpois(0:10,0.5),xlab="",ylab="Prob",type='h',main="Lambda0.5")

>plot(0:10,dpois(0:10,1),xlab="",ylab="Prob",type='h',main="Lambda1")

>plot(0:10,dpois(0:10,2),xlab="",ylab="Prob",type='h',main="Lambda2")

>plot(0:10,dpois(0:10,5),xlab="",ylab="Prob",type='h',main="Lambda5")

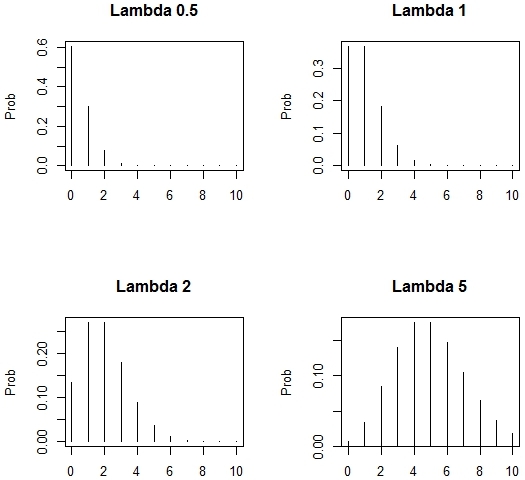
图4-8 具有不同Lambda值的泊松分布值 

毫不奇怪，当泊松分布发生变化时（图4-8）lambda变化看起来很像p变化时二项式的变化。考虑到关系Lambda= n* p，这应该不令人意外。

上面的图只考虑X = x的范围[0，10]，所以在这种情况下Lambda=5有更多的分布向右移动。概率水平到1类似的可以看累积分布（泊松分布函数的ppois）与二项式一样。范围X = x从0到20的所有lambda中使用的值。

> par(mfrow=c(2,2))

>plot(0:20,ppois(0:20,0.5),xlab="",ylab="Cum Prob",type='h', main="Lambda 0.5")

>plot(0:20,ppois(0:20,1),xlab="",ylab="Cum Prob",type='h',main="Lambda 1")

> plot(0:20,ppois(0:20,2),xlab="",ylab="CumProb", type='h',main="Lambda 2")

>plot(0:20,ppois(0:20,5),xlab="",ylab="Cum PRob",type='h',main="Lambda 5")

       

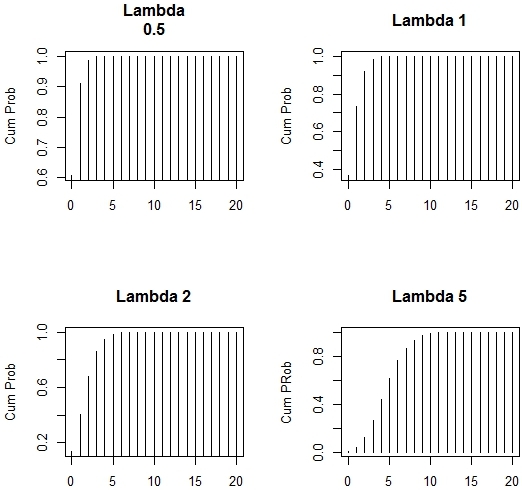
图4-9 具有不同Lambda值的泊松CDF 

对于2或更小的λ值，从CDF图中可以清楚地看到（图4-9）2000 bp中的10个以上不太可能包含错误。尽管x = 10，lambda= 5的图表似乎在1左右平稳，仍然有一些X值获得更大的概率，10以上，可以通过在R中按类似的方法进行一些额外的计算来分析。如下所示：

> ppois(10,5)

[1] 0.9863047

> ppois(12,5)

[1] 0.9979811

> ppois(15,5)

[1] 0.999931

> ppois(20,5)

[1] 1