第三节  区间估计 

与点估计不同，区间估计（Interval Estimation）给出了参数空间中的一个点，但是是一个区间（区域）。根据总体思路，我们似乎总是希望得到一个具体数值的参数，也就是说，使用一个估计点就足够了，为什么我们不得不引入区间估计？这是因为当使用点估计时，我们对估计值是否“接近”实际参数的调查是通过建立各种评估标准，然后根据这些标准进行评估来完成的，这些标准通常描述了大量在数学特征方面进行重复性实验，而估值的可靠性和准确性未得到回答。也就是说，对于这样的问题：“在参数临近估计的概率是多少？”，“这一点估计并没有给出明确的结论，但在某些应用中，正是人们感兴趣的。”

例4.16某厂到工厂估算一批电子设备的平均使用寿命，随机抽样产品进行检测，通过对检测数据的处理来判断批次产品是否合格的结论？并要求这个结论的可信度是95％，这个数据应该如何处理？

至于如何定义“可信程度”，我们会在下面讨论它，但从常识来说，它通常是电子元件的一系列寿命度量标准，不一定是非常准确的数字。因此，在估算这些电子元件的平均预期寿命时，寿命的准确值并不是最重要的，重要的是预计寿命可以在合格产品范围内具有高度的可信度，非常重要的是，它涉及到使用这些电子元件的可靠性。因此，使用点估计不一定达到应用的目的，这需要归纳区间估计。

区间估计大致是两个统计量，（），由[，]确定的区间作为参数值范围的估计值。显然，一般来说这样说并不合理，首先，这个估计必须有一定的精度，也就是说-不能太大，太大不能解释任何问题；其次，估计必须可信，因此-不能太小，太小而不能保证这一要求。例如，从区间[1，100]估计某人的年龄，虽然绝对可信，但不能带来任何有用的信息；相反，如果使用区间[30，31]来估计一个人的年龄，虽然提供了有关该人的年龄的信息，但很难说服人们这个结果的正确性。我们希望能够获得更高的精度和更高的可信度，但是当获得的信息是确定的时候，例如样本大小固定，显然不可能同时达到最优状态。通常采用将可信程度固定到所需水平并尽可能高地获得估计精度范围。区间估计的正式定义如下。

定义4.4 对于参数，如果有两个统计量，，满足对给定的，有

则称区间[，]是的一个区间估计或置信区间（Confidence Interval），，分别称作置信下限（Confidence lower limit）、置信上限（Confidence upper limit），称为置信水平（Confidence level）。

       这里的置信水平，就是对可信程度的度量。置信水平为1-，在实际上可以这样来理解:如取，就是说若对某一参数取100个容量为的样本，用相同方法做100个置信区间。[，]，=1,2,…,100,那么其中有95个区间包含了真参数。因此,当我们实际上只做一次区间估计时，我们有理由认为它包含了真参数。这样判断当然也可能犯错误，但犯错误的概率只有5%.

       下面我们来讨论一下区间估计的一般步骤。

       （1）设欲估参数为，先取的一个点估计，它满足两点：一是它较前面提出的标准应该是一个“好的”估计量，二是它的分布形式应该已知，只依赖未知参数。

       （2）所求的区间考虑为的一个邻域，（或者等等），使得对于

=1-               （4-20）

且一般要求尽可能小。为确定，须用解不等式的方法将（4-20）式中的随机事件变成类似于下述等价形式：

      （4-21）

其中，为可逆的的已知函数，的分布与无关且已知，一般其分位点应有表可查，这是关键的一步。于是就可得出，为某个分位点，如，。

       （3）从，的表达式中解出即可。区间估计涉及到抽样分布，对于一般分布的总体，其抽样分布的计算通常有些困难，因此，我们将主要研究正态总体参数的区间估计问题。

1.单个正态总体参数的区间估计

设为的样本，对给定的置信水平，，我们来分别研究参数与的区间估计。

       例4.17 在上述前提下，求的置信水平为的区间估计。

        解考虑的点估计为，确定使

且使区间长尽可能小。下面分两种情况

（1）已知，变换事件，使表成式（4-21）的形式：

     

          

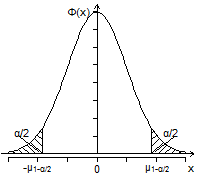
图4-1

这里。为使，又要尽量使最小，亦即使最小，如图4-1，从密度函数的特点来看（对称、原点附近密度最大，往两边密度减小），只有取，即，从而所求的区间是

             （4-22）

 （2）未知，将事件变换成式（4-21）的形式：

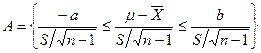
其中由例4.17知，，为使，且区间尽量短。与情形一样，只有取。因此所求区间为

       （4-23）

       例4.18 在上述前提下求的置信水平为1-的区间估计。

       解的点估计量为，注意到，考虑，及的邻域[，]，使

变换事件

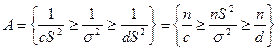
因，故为使，通常取

   

             

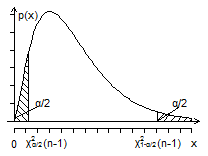
图4-2

于是，所求区间为

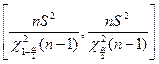
这里要使区间最短，计算太麻烦，因此，在取分位点时采用类似主对称型分布的取法，使密度函数图形两端的尾部面积均为（如图4-2）。

例4.19 一批零件尺寸服从，对进行区间估计（未知），要求估计精度不低于2，置信水平保持为，问至少要抽取多少件产品作为样本？

解显然，此处要求

因，故

                （4-24）

式（4-23）不是的显式，但对于具体数值，可采取“试算法”来确定。一般是先对作个大致估计（可以由以往的经验确定），然后用试算的方式确定适合方程（4-24）的。例如若估计出200，又已知，，来试算：

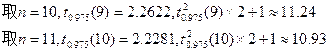
       显然，如果任一正整数不可能严格满足方程（4-24）的话，则应取使式（4-24）左边大于右边的最小的，因此应该取=11。

2.双正态总体参数的区间估计

实际中常有类似于下列的问题。

例4.20 有A、B两种牌号的灯泡各一批，希望通过抽样实验并进行区间估计，考察

       （1）两种灯泡的寿命是否有明显差异；或者考察

       （2）两种灯泡的质量稳定性是否有明显差异。

我们补充一些合理假设，将上述应用问题变为数理统计问题。设A、B种灯泡的寿命分别服从，，并设两种灯泡的寿命是独立的。这就是两正态总体的参数区间估计问题，对于（1）是求的置信区间，对于（2）是求的置信区间。如果在（1）中，区间估计的置信下限大于0，则认为明显大于；若它的置信上限小于0，则认为明显小于；若0含在置信区间内，则认为两者无明显差别。对于（2）也可做类似的讨论，只需将0相应地改为１即可。下面来给出这两个区间估计。不妨设这两种灯泡的样本分别为及，置信水平为1-。

   对于（1），显然可用的点估计量来构造置信区间[，]，其中，满足

   下面分两种情况进行讨论。

   （1）若已知，则变换事件

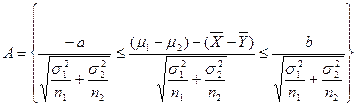
    注意到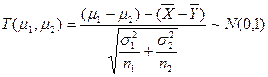,欲使，取

    此时估计区间是

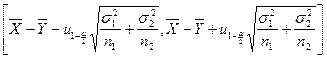
   （2）若未知，只研究的情形，变换事件:

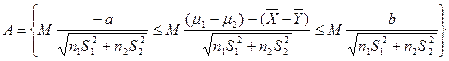
    其中

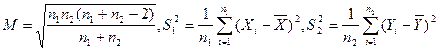
     易知

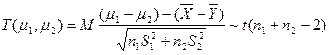
     因此，为使，取

    故所求区间是

             （4-25）

   对于(ii)取

  。

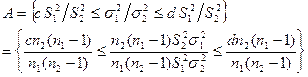
   为使，类似于分布，取分位点

    故所求区间为

   （4-26）

   例4.21 随机选取Ａ种灯泡5只，Ｂ种灯泡7只，做灯泡寿命实验，算得两种牌号的平均寿命分别为=1000（小时），=980（小时）；样本方差=784（小时2），=1024（小时2）。取置信度为0.99，试求关于的区间估计，其中假设。

   解此题中，置信度1-=0.99，即=0.01；。得

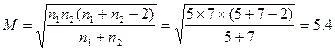
代入（4-25）得的0.99的置信区间为

 因0含在此置信区间内，故认为与无明显差异。