第二节  点估计 

点估计（PointEstimation）：点估计变量是随机变量的一个函数，它本身也是一个随机变量和统计数。点估计量的值随样本的不同而不同，并且有抽样分布。

1.矩估计法（Square Estimation）

矩(moment)分为原点矩和中心矩两种。对于样本，各观测值的k次方的平均值，称为样本的k阶原点矩，记为，有，例如，算术平均数就是一阶原点矩；用观测值减去平均数得到的离均差的k次方的平均数称为样本的k阶中心矩，记为或，有，例如，样本方差就是二阶中心矩。

对于总体，各观测值的k次方的平均值，称为总体的k阶原点矩，记为，有；用观测值减去平均数得到的离均差的k次方的平均数称为总体的k阶中心矩，记为或，有。

所谓矩法就是利用样本各阶原点矩来估计总体相应各阶原点矩的方法，即

         →             （4-7）

并且也可以用样本各阶原点矩的函数来估计总体各阶原点矩同一函数，即若

则

由此得到的估计量称为矩估计量。

例4.7无论总体为什么分布，只要二阶矩存在，则样本方差为方差的矩估计量。

解  设为一样本，我们有

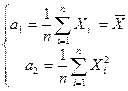
故

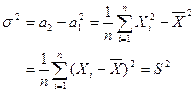
记为。需要估计的参数也可以不是总体的数字特征。

例4.8 现获得正态分布的随机样本，要求正态分布参数和的矩估计量。

首先，求正态分布总体的1阶原点矩和2阶中心矩：

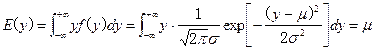
(此处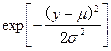表示自然对数底数e的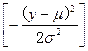的指数式，即)

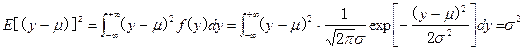
然后求样本的1阶原点矩和2阶中心矩，为

最后，利用矩法，获得总体平均数和方差的矩估计

故总体平均数和方差的矩估计值分别为样本平均数和样本方差，方差的分母为n。

单峰分布曲线还有二个特征数，即偏度(skewness)与峰度(kurtosis)，可分别用三阶中心矩和四阶中心矩来度量。但和是有单位的，为转化成相对数以便不同分布之间的比较，可分别用偏度系数和峰度系数作测度。偏度系数(coefficient of skewness)是指3阶中心矩与标准差的3次方之比；峰度系数(coefficient of kurtosis)是指4阶中心矩与标准差的4次方之比。当偏度为正时，分布偏向大于平均方向，而偏斜度为负，而偏斜度向小于平均数方向偏斜，并且当偏斜度的绝对值大于2时，偏斜度偏斜程度严重。当峰度大于3时，分布更陡峭，峰值状态明显，即总体变量的分布比较集中。

由样本计算的偏度系数

cs=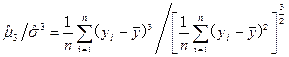           (4-8)

峰度系数

ck=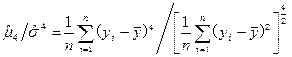           (4-9)

2.最小二乘法（Least Squares）

在许多实际问题中，通常根据实验测量两个变量x和y的一些实验数据(x1,y1),…(xn,yn)，为了建立两个变量函数关系的近似值，近似函数称为经验公式。在两个观测中，往往总有一个量精度比另一个高得多，为简单起见，观测的精度更高，因为没有误差，并且这个观测值被选择为x，并且所有误差仅被认为是y误差。用理论公式推导x和y的函数关系：

                （4-10）

给出，其中是m个要通过实验确定的参数。对于每组观测数据（xi，yi），i＝1，2，…，N。都对应于xy平面上一个点。若不存在测量误差，则这些数据点都准确落在理论曲线上。只要选取m组测量值代入式（4-10），便得到方程组：

                             （4-11）

式中i＝1，2，…，m。求m个方程的联立解即得m个参数的数值。显然N<m时，参数不能确定。

在N>m的情况下，式（4-11）成为矛盾方程组，不能直接用解方程的方法求得m个参数值，只能用曲线拟合的方法来处理。设测量中不存在着系统误差，或者说已经修正，则y的观测值yi围绕着期望值摆动，其分布为正态分布，则yi的概率密度为

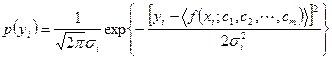
例4.9 用最小二乘法求总体平均数的估计量。

若从平均数为的总体中抽得样本为y1,y2,y3,…,yn，则观察值可剖分为总体平均数与误差ei之和，

总体平均数的最小二乘估计量就是使yi与间的误差平方和为最小，即

为最小。为获得其最小值，求Q对的导数，并令导数等于0，可得：

即总体平均数的估计量为：

因此，算术平均数为总体平均数的最小二乘估计。这与矩法估计是一致的。此处顺便介绍估计离均差平方和的数学期望：

       

              

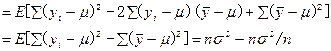
              =(n-1)

因而，估计为：

=

与矩法所得不同，而与常规以自由度为除数法一致。

3.极大似然估计（Maximum Likelihood Estimation）

参数的点估计方法中另一个常用方法就是极大似然估计，简记为。从字面上看，通过对样本的检查，将被评估的参数视为参数的估计，事实上，最大似然估计的原理是相似的。我们用一个具体的例子来说明这个估计的概念。

例4.10 已知甲、乙两射手命中靶心的概率分别为0.9及0.4，今有一张靶纸上面的弹着点表明为10枪6中，已知这张靶纸肯定是甲、乙之一射手所射，问究竟是谁所射？

从直观的角度来看，A的枪法是较优的，达到了0.9的命中率，看来射击效果并不是那么糟糕，而B的射击似乎还不足以达到如此好的效果，但是二者取一，还是更像B 的射击。

我们来计算一下可能性。为此，我们建立一个统计模型：设甲、乙射中与否分别服从参数为的两点分布，今有样本，其中有6个观察值为1，4个为0，由此估计总体的参数是0.9，还是0.4．这里因为参数空间只有两个点：={0.9，0.4}，我们不妨分别计算一下参数为什么的可能性大。若是甲所射，即参数=0.9，则此事发生的概率为

；

若是乙所射，即参数=0.4，则此事发生的概率为

，

尽管是乙所射的可能也不大，但毕竟比是甲所射的概率大了10倍，因此，在参数空间只有两点的情况下，概率的最大值在=0.4处发生，故我们更情愿认为是乙所射，即用0.4作为的估计：==0.4。

       总之，最大似然估计的出发点是基于统计学原理，即一项事件在随机实验中发生，比如已经得到某个具体的样本，则必然认为发生该事件的概率最大。

       从例4.10我们可以看出，极大似然估计的做法，关键有两步：

       第一步写出某样本出现概率的表达式，对于离散型总体，设它的分布列为则上述样本出现的概率为：

       对于固定的样本，是参数的函数，我们称之为似然函数（Likelihood Function）。

       第二步则是求是参空间），使得达到最大，此即为所求的参数的极大似然估计。这里还需要着重强调几点：

（1）当总体是一个连续的随机变量时，谈论样本发生的概率是毫无意义的，因为任何特定样本的发生都是0概率事件。然后我们考虑样本出现在任何小邻域中的概率，概率越大，样本的概率密度越大。因此，在连续型总体的情况下，我们使用样本的密度函数作为似然函数。

   （2）为了计算方便，我们常对似然函数取对数，并称为对数似然函数（Logarithm likelihood function）。易知，与在同一处达到极大，因此，这样做不会改变极大点。

   （3）在例4.10中参数空间只有两点，我们可以用穷举法求出在哪一点上达到最大，但在大多数情形中，包含ｍ维欧氏空间的一个区域，因此，必须采用求极值的办法，即对对数似然函数关于求导，再令之为0，即得

         （4-12）

   我们称（4-12）为似然方程（组）（Likelihood equation（group））。解上述方程，即得到的，．

   例4.11 设是的样本，求与的．

   解 我们有

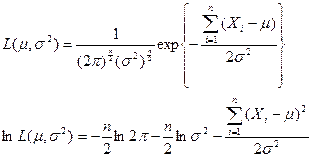
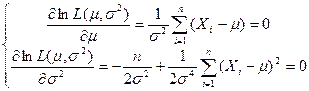
   解似然方程组，即得

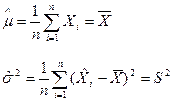
   看来，对于正态分布总体来说，，的矩估计与MLE是相同的。矩估计与MLE相同的情形还有很多。

   例4.12 设有个事件两两互斥，其概率之和为1。做次重复独立实验，则各事件发生的频率为各相应概率的MLE。事实上，设样本记录了每次实验中所发生的事件，以表示次实验中事件发生的次数，则此样本出现的概率（似然函数）为

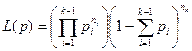
于是

得似然方程

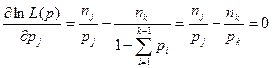
即

将上述个等式相加，注意到及

得到

右边即为事件发生的频率，显然事件与其它事件地位是相同的，故类似可得到

   需注意到，并非每个问题都可通过解似然方程得到，如

   例4.13求均匀分布中参数的。先写出似然函数

       （4-13）

   本例似然函数不连续，不能用似然方程求解的方法，只有回到极大似然估计的原始定义，由式（4-13），注意到最大值只能发生在

                 （4-14）

  时；而欲最大，只有使最小，即使尽可能小，尽可能大，但在式（4-14）的约束下，只能取=，=。

   和矩估计的情形一样，有时虽能给出似然方程，也可以证明它有解，但得不到解的解析表达式。

   例4.14 求柯西分布中的．我们可得似然方程为

这个方程只能求数值解。

例4.15 两个亲本的基因型分别为AABB和aabb，这两个亲本杂交后F2出现了4种基因型，分别为A_B_、A_bb、aaB_和aabb，得到四种基因型的个数分别为c、d、e、f，已知AA和BB两对基因间存在连锁关系，现欲估计重组率？

设重组率为r，根据遗传学推导，可以得到4种基因型的概率见表4-1。

表4-1 F2群体基因型的分离情况                                   

基  因  型	A_B_	A_bb	aaB_	aabb	总数
观察得到基因型个数	c(289)	d(26)	e(29)	f(76)	n(420)
概    率					1

首先，通过表4-2介绍由两对连锁主基因控制的F2群体16种基因型的概率计算出4种表现型的概率（表4-1）。 

表4-2 F2群体的基因型及其概率                                                 

配子及概率	AB	Ab	aB	ab
AB	AABB	AABb	AaBB	AaBb
Ab	AABb	AAbb	AaBb	Aabb
aB	AaBB	AaBb	aaBB	aaBb
ab	AaBb	Aabb	aaBb	aabb

按多项式分布，可以根据概率函数得到似然函数为：

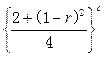
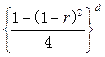
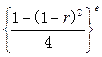
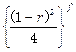 （4-15）

若以代入上式，则似然函数和对数似然函数分别为：

                    （4-16） （k是常数项）  （4-17）

对上式求导数，并令导数为0，可得方程：

上式化解为一元二次方程

            （4-18）

在的两个解中取一个符合遗传规律的解，那么，重组率的解为：。

对于本例，有

 

        =0.1226±0.6140

取正根，=0.7366，由此，=0.142。

统计理论已证明：重组率方差估计量为：

                               （4-19）

对于本例，有