第四章 参数估计方法

学习要求：  理解点估计的概念，掌握矩法、最小二乘法、极大似然法。了解估计量的评选标准（无偏性、有效性、一致性）。理解区间估计的概念，会求单个正态总体的均值与方差的置信区间，会求两个正态总体的均值差与方差比的置信区间。

参数估计（parameter estimation）方法主要适用于我们所知的总分布类型，但一个或几个重要参数是未知的。因此，只要我们通过对样本进行抽样来得到这些参数的估计值，我们就可以确定总体分布。如血球计数或水样中细菌计数，我们知道它的分布应该是泊松分布，所以问题是通过样本确定其参数λ；例如，如果我们想研究某个种群的高度，一般来说这个高度服从正态分布，我们需要从样本中确定两个参数μ和σ2。当然，也有一些我们对整体分布不感兴趣的情况，只要我们知道它的一个或两个重要参数，如均值和方差当然也可以使用参数估计。

参数估计可以分为两种，一种称为点估计(point estimation)，另一种是利用样本构造一个统计量，作为总体参数的估计。因此，只要测量一组样本的值，就可以通过代入统计公式来获得总体参数的估计值。另一种方法称为区间估计（interval estimation），它给出了一系列值，并给出了我们关心的整体参数落入该范围的概率。这个值的范围称为置信区间，并且总体参数落入该范围的概率称为置信度。 

第一节  估计量的评价准则

估计参数估计的准则（Evaluation Rule of Estimator）：参数估计可以以不同的方式使用，后文引入矩法，最小二乘法和最大似然法，并且不同的参数估计量（parameter estimator）可以是通过使用不同的方法获得。各种估计各有其优点。对于均匀分布的Ｕ[]，参数的矩估计与最大似然估计的矩估计不同，即使同样的方法也可能得到不同的统计量。

例4.1设总体服从参数为的泊松分布，即

则易知，，分别用样本均值和样本方差取代和，于是得到的两个矩估计量。

       由于估算结果往往不是唯一的，各估计值各有什么优势？首先有一个标准问题。评估标准主要是无偏性、有效性、最小方差性等。   

1.无偏性（Unbiased）

       定义4.1 设=是的一个估计量，若对任意的，都有，则称是的无偏估计量（Unbiased estimator），如果

则称是的渐近无偏估计量（Approximationunbiased estimator），其中称为是的偏差（affect）。

       无偏性体现了估计量在真相周围摆动的程度，显然我们希望估计值具有无偏性。

       例4.2 是总体期望值的无偏估计，因为

例4.3 不是总体方差的无偏估计，因为注意到

．

故

但                  

 

因此是渐近无偏估计。在的基础上，我们适当加以修正可以得到一个的无偏估计，这个估计量也和样本方差一样是经常被采用的：

        由此例也可以看出，例4.1中关于的两个矩估计量中，是无偏的，；而是有偏的，.

       评估的利弊评估，一般是站在概率论的基础上，在实际应用中包括多次使用这种方法的效果的问题。对于无偏性，情况也是如此，即在实际应用问题中，如果使用此估计值计算多个估计值，则其平均值可能接近估计参数的值。这有时是有意义的，例如，如果制造商长时间向供应商提供产品，并且在产品的测试方法中，双方同意使用样品来估计缺陷产品。如果这个估计是没有偏差的，那么双方都应该能够接受它。例如，这次估计的不合格率很高，制造商遭受损失，但下一次估计可能较低，制造商的损失可以弥补，因为双方之间的交易次数很多，采用无偏估计，一般而言，是相互排斥的。但不幸的是，无偏性有时几乎没有什么实际意义。有两种情况，一种情况是在没有多重抽样的一类实际问题中，比如前面的例子，供应商和分销商没有长期的合作关系，纯粹是一次性的商业行为，双方都不能承担损失，没有什么“平均”说。另一个原因是估计量实际上没有相互补偿，因此“平均”没有实际意义，例如，通过测试某种导弹的系统误差来估计，即使这个估计是无偏的，但如果估计这组导弹的系统误差实际上估计是偏左的，下一批导弹估计是右边的，结果，两批导弹在使用中无法击中预定目标，也没有“左”和“右”，“正确性的”相互抵消或“平均命中”的问题。

我们也可以举出统计数字的例子来说明无偏性的局限性。

例4.4 设服从参数为的泊松分布，为的样本，用作为的估计，则此估计是无偏的。因为

但当取奇数时，＜０，显然用它作为＞０的估计是不能令人接受的。为此我们还需要有别的标准。

2.最小方差性和有效性（Minimum Variance and efficiency）

如前所述，无偏估计仅表明估计的值围绕真相摇摆，但“周边”有多大？我们自然希望摆动的范围越小越好，也就是说，估计量的取值的集中程度要尽可能的高，这是统计最小方差无偏估计的概念。

       定义4.2 对于固定的样本容量，设（）是参数函数的无偏估计量，若对的任一个无偏估计量（）有

则称（）为的（一致）最小方差无偏估计量，简记为UMVUE(Uniformly Minimum VarianceUnbiased Estimation)或者称为最优无偏估计量。

       从定义来看，很难直接验证估计是参数函数的最优无偏估计。但是对于大量的分布和估计，我们从另一个角度来看问题。考虑到所有的无偏估计，如果我们可以在这个类别的无偏估计中找到无偏估计中方差的一个下界（下限显然存在，它可以至少为0，并且可以证明估计能达到这一下界，则当然就是一个UMVUE）。

        我们来求这个下界。下面不妨考虑总体为连续型的。（对于离散型的，只须做一点相应的改动即可），简记统计量（）为，样本的分布密度为；积分为．又假设在以下计算中，所有需要求导和在积分号下求导的场合都具有相应的可行性。今考虑的一个无偏估计，即有

两边对求导

               （4-1）

又

      上式两边对求导

                 （4-2）

式（4-1）加上式（4-2）乘以-

上式改写成

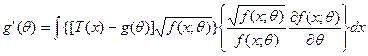
用柯西一许瓦尔兹（Cauchy-Schwarz）不等式，即得

 (6.7)

其中

               （4-3）          （4-4）

       由式（4-2）~式（4-4）即得著名的克拉美-劳（Cramer-Rao）不等式（简称C-R不等式）:

           （4-5）

       注意到独立同分布，则由

      以及当时，利用式（4-2）

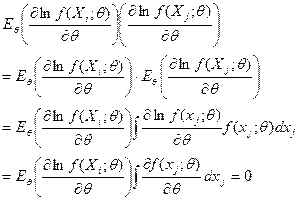
可得

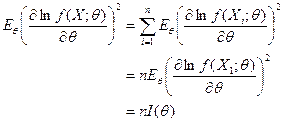
其中=称为费歇信息量(information quantity)，于是式（4-5）可简写成

              （4-6）

式（4-6）的右边称为参数函数估计量方差的C-R下界（lowerlimit）。还可以证明的另一表达式，它有时用起来更方便：

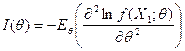
定义4.3 称为的无偏估计量的效率（efficiency）（显然由C-R不等式，）。又当的效率等于１时，称是有效（efficient）的；若，则称是渐近有效（asymptoticallyefficient）的。

显然，有效估计量必是最小方差无偏估计量，反过来则不一定正确，因为可能在某参数函数的一切无偏估计中，找不到达到下界的估计量。我们常用到的几种分布的参数估计量多是有效或渐近有效的。从下面的例子，我们可以体会出验证有效性的一般步骤。

      例4.5 设总体～，为的样本，则的无偏估计是有效的，的无偏估计是渐近有效的。

       证(i) 由例6.13,6.14知,,分别是和的无偏估计。

       (ii) 计算,

易知

又从而

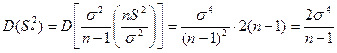
   (iii) 计算

故

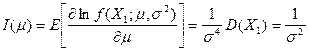
又

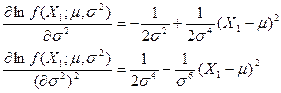
故

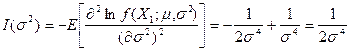
   (iv) 计算效率

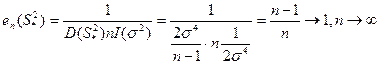
   (v) 故是的有效估计，是的渐近有效估计。

   例4.6 仍考虑例4.1中泊松分布参数的矩估计量=的有效性（由于不是无偏估计，不考虑其有效性）。注意，对离散型总体，在考虑费歇信息量时用概率分布来取代概率密度，故有

    故

    从而效率

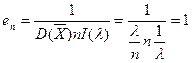
    它是有效的，从而也是最小方差无偏估计量。