第四节  正态分布

如果随机变量的概率密度为

；               

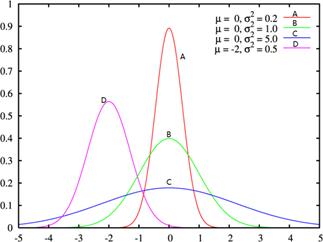
图3-2 正态分布密度曲线

其中s > 0，s，m为常数，则称X服从参数为s，m的正态分布（normal distribution），记为。 

易证（略）：

        （1）

        （2）

特别的，当m=0，s =1时，称为标准正态分布，其概率密度为

正态分布具有以下几个重要特征：

（1）正态分布密度曲线是单峰、对称的悬钟形曲线，对称轴为x=μ；

（2）f(x)在x=μ处达到极大，极大值；                                    

（3）f(x)是非负函数，以x轴为渐近线，分布从-∞至+∞；

（4）曲线在x=μ±σ处各有一个拐点，即曲线在(-∞,μ-σ)和(μ+σ,+∞) 区间上是下凸的，在[μ-σ,μ+σ]区间内是上凸的；   

（5）正态分布有两个参数，即平均数μ和标准差σ。μ是位置参数，如图  

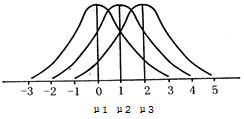
图3-3 σ相同而μ不同的三个正态分布

图3-4 μ相同而σ不同的三个正态分

3-3所示。当σ恒定时，μ愈大，则曲线沿x轴愈向右移动；反之，μ愈小，曲线沿x轴愈向左移动。σ是变异度参数，如图3-4所示，当μ恒定时，σ愈大，表示x的取值愈分散，曲线愈“胖”；σ愈小，x的取值愈集中在μ附近，曲线愈“瘦”。        

标准正态分布的概率计算，设u服从标准正态分布，则u在[u1,u2]内取值的概率为：

          

   =Φ(u2)－Φ(u1)                          （3-11）

而Φ(u1)与Φ(u2)可由附表1查得。

附表1只对于-4.99≤u＜4.99给出了Φ(u)的数值。表中，u值列在第一列和第一行，第一列列出u的整数部分及小数点后第一位，第一行为u的小数点后第二位数值。例如，u=1.75，1.7放在第一列，0.05放在第一行。在附表1中，1.7所在行与0.05所在列相交处的数值为0.95994，即Φ(1.75)=0.95994。有时会遇到给定Φ(u)值，例如Φ(u)=0.284，反过来查u值。这只要在附表1中找到与0.284最接近的值0.2843，对应行的第一列数-0.5，对应列的第一行数值0.07，即相应的u值为u=-0.57，亦即Φ(-0.57)=0.284。如果要求更精确的u值，可用线性插值法计算。

表中用了象.032336，.937674这种写法，分别是0.0002326和0.9997674的缩写，03表示连续3个0，93表示连续3个9。

由(3-11)式及正态分布的对称性可推出下列关系式，再借助附表1，便能很方便地计算有关概率：

        P(0≤u＜u1)＝Φ(u1)-0.5               

        P(u≥u1)=Φ(-u1)                     

 P(｜u｜≥u1)=2Φ(-u1)                  (3-12)

        P(｜u｜＜u1)=1-2Φ(-u1)              

        P(u1≤u＜u2)＝Φ(u2)-Φ(u1)   

例3.14 已知u～N(0，1)，试求：(1) P(u＜-1.64)；(2) P (u≥2.58)；(3) P (｜u｜≥2.56)；(4) P(0.34≤u＜1.53)。

利用(3-12)式，查附表1得：

       (1) P(u＜-1.64)=0.05050

       (2) P (u≥2.58)=Φ(-2.58)=0.024940

       (3) P (｜u｜≥2.56)=2Φ(-2.56)=2×0.005234=0.010468

       (4) P (0.34≤u＜1.53)=Φ(1.53)-Φ(0.34)=0.93669-0.6331=0.30389

        关于标准正态分布，以下几种概率应当熟记：

P（-1≤u＜1）=0.6826

P（-2≤u＜2）=0.9545

P（-3≤u＜3）=0.9973

P（-1.96≤u＜1.96）=0.95

P (-2.58≤u＜2.58)=0.99                

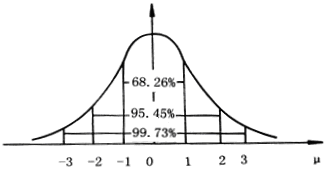
图3-5 标准正态分布的三个常用概率 

u变量在上述区间以外取值的概率分别为：

P(｜u｜≥1)=2Φ(-1)=1- P(-1≤u＜1)=1-0.6826=0.3174

P(｜u｜≥2)=2Φ(-2)=1- P（-2≤u＜2）=1-0.9545=0.0455

P(｜u｜≥3)=1-0.9973=0.0027

P(｜u｜≥1.96)=1-0.95=0.05

P(｜u｜≥2.58)=1-0.99=0.01

正态分布密度曲线和横轴围成的一个区域，其面积为1，这实际上表明了“随机变量x取值在-∞与+∞之间”是一个必然事件，其概率为1。若随机变量x服从正态分布N(μ,σ2)，则x的取值落在任意区间[x1,x2）的概率，记作P(x1≤x＜x2)，等于图3-6中阴影部分曲边梯形面积。即：

             (3-13)

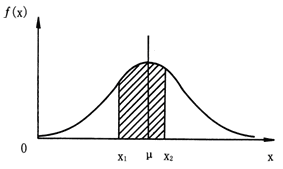
图3-6 正态分布的概率

     对 (4-13)式作变换u=(x-μ)／σ，得dx=σdu，故有

                  =

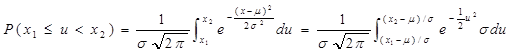
其中，

这表明服从正态分布N(μ,σ2)的随机变量x在[x1，x2）内取值的概率，等于服从标准正态分布的随机变量u在[(x1-μ)/σ,(x2-μ)/σ）内取值的概率。因此，计算一般正态分布的概率时，只要将区间的上下限作适当变换（标准化），就可用查标准正态分布的概率表的方法求得概率了。

例3.15设x服从μ=30.26,σ2=5.102的正态分布，试求P(21.64≤x＜32.98)。

 令，则u服从标准正态分布，故

                   =P(-1.69≤u＜0.53)=Φ(0.53)-Φ(-1.69)

                   =0.7019-0.04551=0.6564

       关于一般正态分布，以下几个概率（即随机变量x落在μ加减不同倍数σ区间的概率）是经常用到的。

P(μ-σ≤x＜μ+σ)=0.6826

P(μ-2σ≤x＜μ+2σ) =0.9545

P (μ-3σ≤x＜μ+3σ) =0.9973

P (μ-1.96σ≤x＜μ+1.96σ) =0.95

P (μ-2.58σ≤x＜μ+2.58σ)=0.99

上述关于正态分布的结论，可用一实例来印证。126头基础母羊体重资料的次数分布接近正态分布，现根据其平均数=52.26(kg)，标准差S=5.10(kg)，算出平均数加减不同倍数标准差区间内所包括的次数与频率，列于表3-1。 

表3-1 126头基础母羊体重在±kS 区间内所包括的次数与频率                                                             

±kS	数值	区  间	区间内所包含的次数与频率
			次数	频率（%）
±1S	52.26±5.10	47.16―57.36	84	67.46
±2S	52.26±10.20	42.06―62.46	119	94.44
±3S	52.26±15.30	36.96―67.56	126	100.00
±1.96S	52.26±10.00	42.26―62.26	119	94.44
±2.58S	52.26±13.16	39.10―65.42	126	100.00

由表3-1可见，实际频率与理论概率相当接近，说明126头基础母羊体重资料的频率分布接近正态分布，从而可推断基础母羊体重这一随机变量很可能是服从正态分布的。

生物统计中，不仅注意随机变量x落在平均数加减不同倍数标准差区间(μ-kσ,μ+kσ)之内的概率而且也很关心x落在此区间之外的概率。我们把随机变量x落在平均数μ加减不同倍数标准差σ区间之外的概率称为双侧概率(两尾概率)，记作α。对应于双侧概率可以求得随机变量x小于μ-kσ或大于μ+kσ的概率，称为单侧概率（一尾概率），记作α／2。例如，x落在(μ-1.96σ,μ+1.96σ)之外的双侧概率为0.05，而单侧概率为0.025。即

P(x＜μ-1.96σ)= P(x＞μ+1.96σ)=0.025

双侧概率或单侧概率如图3.7所示。x落在(μ-2.58σ,μ+2.58σ)之外的双侧概率为0.01，而单侧概率

P(x＜μ-2.58σ)=P(x＞μ+2.58σ)=0.005                

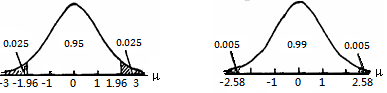
图3-7双侧概率与单侧概率

附表2给出了满足P (｜u｜＞)=α的双侧分位的数值。因此，只要已知双侧概率α的值，由附表2就可直接查出对应的双侧分位数，查法与附表1相同。例如，已知u～N(0,1)试求：

  (1) P(u＜-)+P(u≥)=0.10的

         (2) P(-≤u＜﹚=0.86的

因为附表2中的α值是：

所以  

（1） P(u＜-)+ P(u≥)=1- P(-≤u＜﹚=0.10=α

由附表2查得： =1.644854

（2）P (-≤u＜)=0.86 ，α=1- P (-≤u＜)=1-0.86=0.14

由附表2查得：=1.475791

对于x～N(μ,σ2)，只要将其转换为u～N(0,1)，即可求得相应的双侧分位数。

例3.16已知猪血红蛋白含量x服从正态分布N(12.86，)，若P(x＜) =0.03, P(x≥)=0.03，求、。

由题意可知，α／2=0.03，α=0.06 又因为 

 

P(x≥)=

故P(x＜＝+ P(x≥)= P(u＜-＝+ P(u≥) =1- P(-≤P＜)=0.06=α

由附表2查得：=1.880794,所以

        (-12.86)/1.33=-1.880794， (-12.86)/1.33=1.880794

即≈10.36，≈15.36。