第五节  一些重要的概率分布 

1.n重伯努利实验、二项分布

设实验E只有两个可能的结果：成功和失败，或记为A和，则称E为伯努利（Bernoulli）实验。将伯努利实验独立重复地进行n次，称为n重伯努利实验。

    设一次伯努利实验中，A发生的概率为p（0<p<1），又设X表示n重伯努利实验中A发生的次数，那么，X所有可能取的值为0，1，2，…，n，且

，(k= 0，1，2，…，n)。

易知：

        (1)

        (2)

        所以，，(k= 0，1，2，…，n)是X的分布律。

        如果随机变量X所有可能取的值为0，1，2，…，n，它的分布律为，（k = 0，1，2，…，n），其中0< p< 1为常数，则称X服从参数为n，p的二项分布（binomial distribution），记为X～B(n，p)。

        二项分布是一种常用的离散型分布，例如，

        检查10个产品，不合格产品的个数，其中p为不合格率；

        调查50个人，患色盲的人数，其中p为色盲率；

        射击4次，射中的次数，其中p射中率；等等。

        当n= 1时，，k=0，1。

或写成           

X	0	1
pk	1-p	p

此时称，X服从参数为p的0-1分布（伯努利分布）。容易验证，二项分布具有概率分布的一切性质，即：

（1）P(x=k)= Pn(k)   (k=0,1,…，n)

（2）二项分布的概率之和等于1，即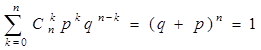

（3）               

（4）            

（5）（m1<m2）   

例3.17纯种白猪与纯种黑猪杂交，根据孟德尔遗传理论，子二代中白猪与黑猪的比率为3:1。求窝产仔10头，有7头白猪的概率。根据题意，n=10，p=3／4=0.75，q=1／4=0.25。设10头仔猪中白色的为x头，则x为服从二项分布B(10，0.75)的随机变量。于是窝产10头仔猪中有7头是白色的概率为：

例3.18设在家畜中感染某种疾病的概率为20％，现有两种疫苗，用疫苗A注射了15头家畜后无一感染，用疫苗B注射15头家畜后有1头感染。设各头家畜没有相互传染疾病的可能，问：应该如何评价这两种疫苗?

假设疫苗A完全无效，那么注射后的家畜感染的概率仍为20％，则15头家畜中染病头数x=0的概率为

同理，如果疫苗B完全无效，则15头家畜中最多有1头感染的概率为

由计算可知，注射A疫苗无效的概率为0.0352，比B疫苗无效的概率0.1671小得多。因此，可以认为A疫苗是有效的，但不能认为B疫苗也是有效的。

        例3.19仔猪黄痢病在常规治疗下死亡率为20％，求5头病猪治疗后死亡头数各可能值相应的概率。

       设5头病猪中死亡头数为x，则x服从二项分布B(5,0.2)，其所有可能取值为0，1，…，5，按二项分布性质（4）式计算概率用分布列表示如下：

      0           1           2           3          4          5

      0.3277  0.4096  0.2048  0.0512  0.0064 0.0003

从上面各例可看出二项分布的应用条件有三：（1）各观察单位只具有互相对立的一种结果，如阳性或阴性，生存或死亡等，属于二项分类资料；（2）已知发生某一结果（如死亡）的概率为p，其对立结果的概率则为1-P=q，实际中要求p是从大量观察中获得的比较稳定的数值；（3）n个观察单位的观察结果互相独立，即每个观察单位的观察结果不会影响到其它观察单位的观察结果。

前面已经指出二项分布由两个参数n和p决定。统计学证明，服从二项分布B(n,p)的随机变量之平均数μ、标准差σ与参数n、p有如下关系：

        当实验结果以事件A发生次数k表示时

μ=np                            (3-14)

σ=                         (3-15)

例3.20 求例3.17平均死亡猪数及死亡数的标准差。

以p=0.2，n=5代入(3-14)和(3-15)式得

平均死亡猪数 μ=5×0.20=1.0(头)

标准差σ== =0.894(头)

当实验结果以事件A发生的频率k／n表示时

                       (3-16)

=                   (3-17)

        也称为总体百分数标准误，当p未知时，常以样本百分数来估计。此时(4-21) 式改写为：

Sp =                   (3-18)

称为样本百分数标准误。

2.泊松分布

如果随机变量的分布律为：

其中是常数，则称服从参数为的泊松分布（Poisson distribution），记为。

        泊松分布在各领域中有着广泛的应用，它常与单位时间（单位面积\单位产品等）上的计数过程相联系，例如，

    某单位时间内电话机接到的呼唤次数；

    某单位时间内候车的乘客数；

    放射性物质在某单位时间内放射的粒子数；

    某页书上的印刷错误的个数；             

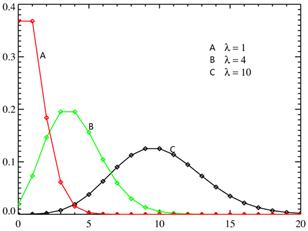
 图3.8 泊松分布概率密度函数

1平方米内，玻璃上的气泡数等等都可以用泊松分布来描述。

        例3.21 某商店出售某种商品。根据经验，此商品的月销售量服从的泊松分布。问在月初进货时要库存多少件此种商品，才能以99%的概率满足顾客要求？

        解：设月初库存件，依题意

那么

        查附表3，可知最小应是8，即月初进货时要库存8件此种商品，才能以99%的概率满足顾客要求。

        泊松定理：设随机变量服从二项分布，且（是常数），则有

。

        证明：令，有

=

        对任意固定的k，当时

，，

       及

所以

        在应用中，当很大()，且很小()时，就可以用以下的泊松分布近似公式

       其中，而关于的值，可以查表（见附表3）。

       例3.22 调查某种猪场闭锁育种群仔猪畸形数，共记录200窝，畸形仔猪数的分布情况如表3-2所示。试判断畸形仔猪数是否服从泊松分布。

表3-2  畸形仔猪数统计分布                           

每窝畸形数k	0	1	3	3	≥4	合计
窝数 f	120	62	15	2	1	200

根据泊松分布的平均数与方差相等这一特征，若畸形仔猪数服从泊松分布，则由观察数据计算的平均数和方差就近于相等。样本均数和方差S2计算结果如下：

=Σfk/n=(120×0+62×1+15×2+2×3+1×4)/200=0.51

=0.51，S2=0.52,这两个数是相当接近的，因此可以认为畸形仔猪数服从泊松分布。

        λ是泊松分布所依赖的唯一参数。λ值愈小分布愈偏倚，随着λ的增大，分布趋于对称（如图3.8所示）。当λ=20时分布接近于正态分布；当λ=50时，可以认为泊松分布呈正态分布。所以在实际工作中，当λ≥20时就可以用正态分布来近似地处理泊松分布的问题。

3.几何分布

从一批次品率为（）的产品中逐个地随机抽取产品进行检验，验后放回再抽取下一件，直到抽到次品为止。设检验的次数为，则可能取的值为1，2，3，…，其概率分布为：

，                

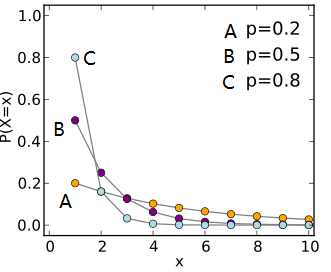
图3-9 几何分布概率密度函数

称这种概率分布为几何分布（geometry distribution）。 

4.超几何分布

设一批产品共有个，其中有个次品，现从中任取个（），则这个产品中所含的次品数是一个离散型随机变量，所有可能的取值为0，1，2，…， ，（其中），其概率分布为：

 （=0,1,2,…, ）

称之为超几何分布（super geometry distribution）。

5.均匀分布

如果随机变量的概率密度为

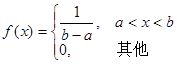
则称X服从(a，b)上的均匀分布（uniformdistribution）。                

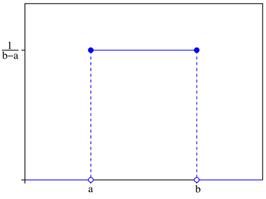
      图3-10 均匀分布的概率密度函数 

如果服从(a，b)上的均匀分布，那末，对于任意满足的，应有

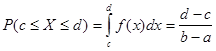
该式说明X取值于(a，b)中任意小区间的概率与该小区间的长度成正比，而与该小区间的具体位置无关。这就是均匀分布的概率意义。

6.指数分布

如果随机变量的概率密度为

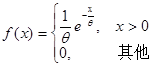
其中为常数，则称服从参数为的指数分布（index distribution）。

       指数分布也被称为寿命分布，如电子元件的寿命，电话通话的时间，随

机服务系统的服务时间等都可近似看作是服从指数分布的。

       指数分布具有无记忆性，即

        

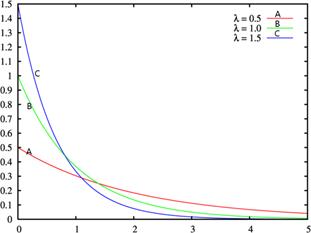
图3-11 指数分布的概率密度函数        

7.二维均匀分布

设为二维随机变量，是平面上的一个有界区域，其面积为，又设

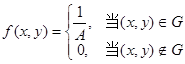
若的密度为上式定义的函数，则称二维随机变量在上服从二维均匀分布(two-dimension uniform distribution)。

可验证满足概率密度的基本性质。

8.二维正态分布 

若二维随机变量的概率密度为：

（  ）

 其中都是常数，且，则称服从二维正态分布(two-dimension normal distribution)。

可以证明满足概率密度的两条基本性质。

        9.多项分布

        在二项分布中，一次随机实验的结果只有两种。一般的，设一次随机实验的结果有l种，即

一次实验中出现事件的概率为

，

显然应满足

作n次独立的随机实验E，事件出现次，的概率分布可表示为

              （3-19）

上式是展开式的一般项，它称为随机变量的参数n和的多项分布（multinomialdistribution），这l个值并不全部独立，它们必须满足下述条件：

显而易见，二项分布是的多项分布之特例。

       多项分布的一些性质举例如下：

       均值

       方差

协方差

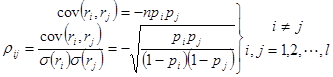      （3-20）

10.负二项分布

满足以下条件的称为负二项分布（negative binomial distribution）：

（1）实验包含一系列独立的实验；

（2）每个实验都有成功、失败两种结果；

（3）成功的概率是恒定的；

（4）实验持续到r次成功，r为正整数。

当r是整数时，负二项分布又称帕斯卡分布，其概率密度函数为：

            （3-21）

       它表示，已知一个事件在伯努利实验中每次的出现概率是p，在一连串伯努利实验中，一件事件刚好在第r + k次实验出现第r次的概率。

取r = 1，负二项分布等于几何分布。其概率密度函数为：

                  （3-22）

举例说，若我们掷骰子，掷到一即视为成功。则每次掷骰的成功率是1/6。要掷出三次一，所需的掷骰次数属于集合 { 3, 4, 5, 6, ... } 。掷到三次一的掷骰次数是负二项分布的随机变量。要在第三次掷骰时，掷到第三次一，则之前两次都要掷到一，其概率为(1 / 6)。注意掷骰是伯努利实验，之前的结果不影响随后的结果。

若要在第四次掷骰时，掷到第三次一，则之前三次之中要有刚好两次掷到一，在三次掷骰中掷到2次1的概率为：

第四次掷骰要掷到一，所以要将前面的概率再乘(1/6)：

11.伽马分布

设随机变量X概率密度函数可表示为：

       （3-23）

为正常数，则称X服从参数的伽马分布（Gamma distribution）。Gamma分布中的参数，称为形状参数（shapeparameter），称为尺度参数（scaleparameter）。它的其他性质举例如下：

      均值 

      方差 

偏度 

峰度 

式（3-23）中的是伽马函数，伽马分布的名称即来源于此。它的显著表达式为：

它有以下性质：

，，

，

，n为正整数

         伽马分布的概率密度函数见图3-12。当时，函数单调下降；当时，概率密度为单峰函数，极大值在处。 

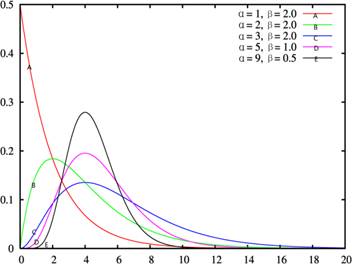
图3-12 伽马分布的概率密度函数 

当两随机变量服从伽马分布，互相独立，伽马分布具有加成性：

    

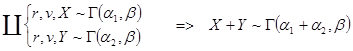
12、柯西分布

      若随机变量X的概率密度为

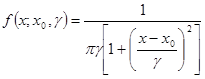
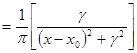                （3-24）

称X服从柯西分布（Cauchy distribution）或布雷特-维格纳（Breit-Wigner）分布。其中x0是定义分布峰值位置的位置参数，γ是最大值一半处的一半宽度的尺度参数。x0=0且γ=1的特例称为标准柯西分布，其概率密度函数为

              （3-25）

从严格的数学意义上，标准柯西分布的各阶矩都是发散的，因为极限值

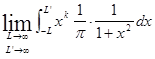
不存在。因此，柯西分布的数学期望和方差都无定义。   

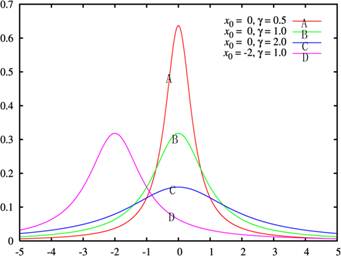
图3-13 柯西分布的概率密度函数（其中B线为标准柯西分布） 

13.分布

卡方分布（Chi-square distribution）是概率论与统计学中常用的一种概率分布。k个独立的标准正态分布变量的平方和服从自由度为k的卡方分布。卡方分布常用于假设检验和置信区间的计算。

若来自正态总体的k个随机变量相互独立，且数学期望为0，方差为1（即服从标准正态分布），则随机变量X

被称为服从自由度为k的卡方分布，记作

卡方分布的概率密度函数为：

               （3-26）

其中x≥0，当x≤0时。这里Γ代表Gamma函数。卡方分布的累积分布函数为：

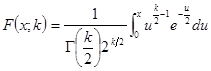              （3-27）

它的其他性质举例如下：

       期望值：k

       中位数：约k-2/3

       众数：k-2，如果

       方差：2k

偏度：    

峰度：12/k  

       

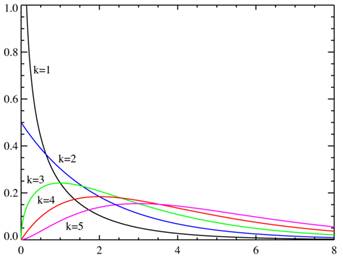
图3-14 卡方分布的概率密度函数 

14.t分布

由样本平均数抽样分布的性质知道：若x～N(μ, σ2)，则～N(μ, σ2/n)。将随机变量标准化得：，则u～N(0,1)。当总体标准差σ未知时，以样本标准差S代替σ所得到的统计量记为t。在计算时，由于采用S来代替σ，使得t变量不再服从标准正态分布，而是服从t分布(t-distribution)。它的概率分布密度函数如下：

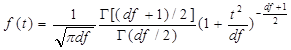          （3-28）

 式中，t的取值范围是（-∞，+∞），df=n-1为自由度。

t分布的平均数和标准差为：

       μt＝0 (df>1)，  (df>2)           （3-29）

        t分布密度曲线如图3-15所示，其特点是：

        （1）t分布受自由度的制约，每一个自由度都有一条t分布密度曲线。

        （2）t分布密度曲线以纵轴为对称轴，左右对称，且在t＝0时，分布密度函数取得最大值。

        （3）与标准正态分布曲线相比，t分布曲线顶部略低，两尾部稍高而平。df越小这种趋势越明显。df越大，t分布越趋近于标准正态分布。当n>30时，t分布与标准正态分布的区别很小；n >100时，t分布基本与标准正态分布相同；n→∞时，t分布与标准正态分布完全一致。

  t分布的累积概率分布函数为：

             (3-30)

因而t在区间（t1，+∞）取值的概率-右尾概率为1-F t (df)。由于t分布左右对称，t在区间（-∞，-t1）取值的概率也为1-F t (df)。于是t分布曲线下由-∞到- t 1和由t 1到+∞两个相等的概率之和-两尾概率为2(1-F t(df))。对于不同自由度下t分布的两尾概率及其对应的临界t值已编制成附表3，即t分布表。该表第一列为自由度df，表头为两尾概率值，表中数字即为临界t值。

例如，当df=15时，查附表3得两尾概率等于0.05的临界t值为 =2.131，其意义是：P(-∞<t<-2.131)=P(2.131<t<+∞)=0.025；P(-∞<t<-2.131)+P(2.131<t<+∞)=0.05。

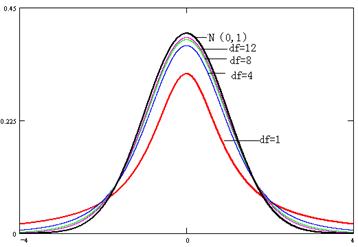
图3-15 t分布的概率密度函数   

由附表3可知，当df一定时，概率P越大，临界t值越小；概率P越小，临界t值越大。当概率P一定时，随着df的增加，临界t值在减小，当df=∞时，临界t值与标准正态分布的临界u值相等。     

15.F分布

F分布（F-distribution）是以统计学家R.A.Fisher姓氏的第一个字母命名的。F分布定义为：设X、Y为两个独立的随机变量，X服从自由度为m的卡方分布，Y服从自由度为n的卡方分布，这2 个独立的卡方分布被各自的自由度除以后的比率这一统计量的分布即F=（x/m）/(y/n)服从自由度为（m，n)的F-分布，上式F服从第一自由度为m，第二自由度为n的F分布。

即设U1和U2分别为自由度n1和n2的2变量：U1~ 2（n1），U2~ 2（n2），并且U1，U2相互独立，则称随机变量

服从自由度（n1，n2）的F分布，记Y~F（n1，n2），其概率密度为：

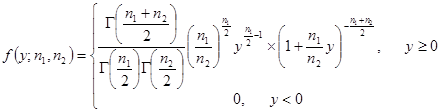     （3-31）

        F分布有如下性质：

      （1）当，是单调下降函数；时，为一单峰函数，概率密度极大值对应的变量为，且。

      （2）均值和方差

       （3）F分布只存在阶原点矩，其表达式是

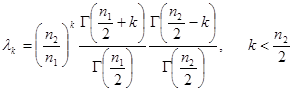
        （4）由F分布的定义可知，随机变量服从自由度n1，n2的F分布

        （5）当，F分布简化为

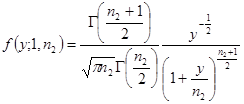
  令，上式正是自由度n2的t分布概率密度，因此，

（6）当n1为某个固定值，的极限情形下，的概率密度

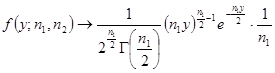
与的概率密度表达式对照可知

        （7）当，时，F分布趋近于正态分布。

在F分布的定义中，若U1用U1’代替，U1’服从自由度n1,，非中心参数λ的分布，则随机变量

服从自由度n1，n2，非中心参数λ的非中心F分布，记为。它的概率密度为：

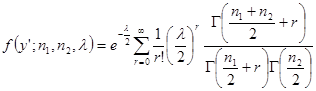
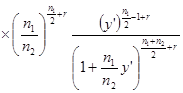              （3-32）

均值和方差为：

             （3-33）

  （3-34）

     当λ=0，非中心F分布简化为一般的（中心）F分布。

      现将各种常见分布间的相互关系和极限性质归纳于图3-16。

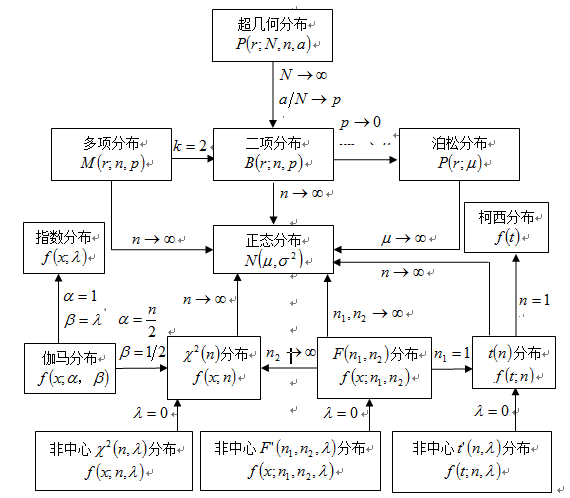
图3-16 各种常见分布间的相互关系和极限性质图