第三节 二维随机变量 

1.二维随机变量及分布函数

在实际问题中，一些实验的结果需要用两个或更多个随机变量来描述。例如，炮弹射弹的位置将由其水平和垂直坐标确定。又如，在制定中国服装标准时，我们需要考虑到体长，手臂长度，胸围，下肢长度，腰围，臀围等变量。通常在相同实验结果的随机变量之间存在关联，因此需要将它们作为整体进行研究。本章只描述二维情况，内容可以扩展到两个以上的维度。

设为随机实验的样本空间，,是定义在上的随机变量，则称有序数组为二维随机变量或称为二维随机向量，称的取值规律为二维分布（two-dimensiondistribution）。

设是二维随机变量，对于任意实数，称二元函数为二维随机变量的分布函数，或称为的联合分布函数（unitydistribution function）。

如果把二维随机变量看作平面上具有随机坐标的点，那末分布函数在（）处的函数值就是随机点落在以点（）为顶点而位于该点左下方的无穷矩形域内的概率。

二维随机变量的分布函数的性质：

(1) ；

(2) 是变量的不减函数，即：对于任意固定的，当时有 ；对于任意固定的，当时有 。

(3) 对于任意固定的，；对于任意固定的，，并且，。

2.二维离散型随机变量的概率分布

如果一个二维随机变量可能只取一个有限值或可以列出的值，则称它为一个二维离散型随机变量（two-dimensiondiscrete random variable）。显然，如果它是一个二维离散随机变量，是一维离散随机变量，反之亦然。

设二维随机变量所有可能取的值为，则称

为的概率分布，或称为的联合分布（unity distribution）。

二维离散型随机变量的联合分布有时也用如下的概率分布表来表示：       

	…    ...
.     .	...     ...         ...    ...   ...     ...     ...    ...  ...         ...     ...   ...     ...     ...    ...  ...

显然，具有以下性质：

        (1) 1,2,…）；

        (2) ；

        (3) 如果是二维离散型随机变量，那末它的分布函数可按下式求得：，这里和式是对一切满足不等式，的来求和的。

例3.9 1个口袋中有大小形状相同的2红、4白6个球，从袋中不放回地取两次球。设随机变量

，

。

求(的分布律及。

解：利用概率的乘法公式及条件概率定义，可得二维随机变量(X,Y)的联合分布律

把的联合分布律写成表格的形式：                 

Y   X	0	1
0	1/15	4/15
1	4/15	2/5

 。

3.二维连续型随机变量的概率分布

设是二维随机变量，如果存在一个非负函数，使得对于任意实数，都有

则称是二维连续型随机变量，函数称为二维连续型随机变量的分布密度，或称为的联合密度。

二维分布密度具有以下性质：

       (1) ；

       (2) ；

(3) ，其中D为XOY平面上的任意一个区域；

       (4) 如果二维连续型随机变量的密度连续，的分布函数为，则

    二元函数在几何上表示一个曲面，通常称这个曲面为分布曲面(distribution curved surface)。由性质(2)知，介于分布曲面和平面之间的空间区域的全部体积等于1；由性质(3)知，落在区域内的概率等于以为底、曲面为顶的柱体体积。

    这里的性质(1)，(2)是概率密度的基本性质。我们不加证明地指出：任何一个二元实函数，若它满足性质(1)、(2)，则它可以成为某二维随机变量的概率密度。

4.边缘分布

作为的整体的二维随机变量的取值情况，可由它的联合分布函数为或它的联合密度函数全面地描述。由于都是随机变量，因此也可以单独考虑某一个随机变量的概率分布问题。

设是二维随机变量，称分量的概率分布为关于的边缘分布；分量的概率分布为关于的边缘分布（marginal distribution）。

由于的联合分布全面的描述了的取值情况，因此，当已知的联合分布时，是容易求得关于或关于的边缘分布。离散随机变量边缘分布律：

设二维随机变量的分布律为，则随机变量关于的边缘分布律如下：

 

        同样得到关于的边缘分布律：

，.

常记

,   ,

连续随机变量边缘概率密度：设是的联合密度函数，则

与一维随机变量概率密度的定义比较，易知X的概率密度为

同样可得Y的概率密度为

和分别称为关于的边缘概率密度。

例3.10 一整数N等可能的在 十个值中取一个值。设D=D（N）是能够整除N的正整数的个数，F=F（N）是能整除N的素数的个数。试写出D和F的联合分布率，并求边缘分布律。

      解：                                                                 

样本点	1	2	3	4	5	6	7	8	9	10
D	1	2	2	3	2	4	2	4	3	4
F	0	1	1	1	1	2	1	1	1	2

由此得到D和F的联合分布率和边缘分布率：                                                           

D   F	1	2	3	4
0	1/10	0	0	0	1/10
1	0	4/10	2/10	1/10	7/10
2	0	0	0	2/10	2/10
	1/10	4/10	2/10	3/10	1

或将边缘分布律表示为                   

D	1	2	3	4
Pk	1/10	4/10	2/10	3/10

               

F	0	1	2
Pk	1/10	7/10	2/10

5.条件分布与随机变量的独立性

设是一个随机变量，其分布函数为

若另外有一事件已经发生，并且的发生可能会对事件发生的概率产生影响，则对任一给定的实数，记

并称为在发生的条件下，的条件分布函数（conditional distribution function）。

设是随机变量所生成的事件：，且，则有

通常，由于随机变量的相关性，随机变量的值可能会影响另一个随机变量值的统计规律性。在这种情况下，随机变量和所谓的“独立性”之间不存在这种效应，我们引入以下定义。

设随机变量的联合分布函数为，边缘分布函数为、，若对任意实数x、y，有

即

则称随机变量和相互独立。

关于随机变量的独立性，有下列两个定理。

定理1 随机变量与相互独立的充要条件是所生成的任何事件与生成的任何事件独立，即，对任意实数集A、B有

定理2 如果随机变量与相互独立，则对任意函数，均有，相互独立。

设是二维离散型随机变量，其概率分布为

则由条件概率公式，当，有

称其为在条件下随机变量的条件概率分布。

对离散型随机变量，其独立性的定义等价于：

若对的所有可能取值 有

即 

       

则称和相互独立。

      连续型随机变量的条件密度与独立性。设二维连续型随机变量的概率密度为，边缘概率密度为，，则对一切使的，定义在的条件下的条件概率密度为：

类似地，对一切使的，定义在的条件下的条件密度函数为：

注：关于定义表达式内涵的解释，以

为例。在上式左边乘以，右边乘以即得

换句话说，对很小的和，表示已知取值于和之间的条件下， 取值于和之间的条件概率。

对二维连续型随机变量，其独立性的定义等价于：

若对任意的x、y，有

几乎处处成立，则称X、Y相互独立。

注：这里“几乎处处成立”的含义是：在平面上除去面积为0的集合外，处处成立。

例3.11 已知随机向量（X，Y）的分布如下表，求x=1条件下Y的分布列?                                       

y   x	1	2	3	4
0	0	1/16	0	3/16
1	1/8	1/8	1/16	0
2	1/16	1/16	3/16	1/8

解：

          

             

      6.协方差和相关系数

      对于，平均数、方差等数字特征不能反映与之间的关系。现引入另一个数字特征专门反映与之间的关系信息：协方差（covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

             （反映的取值与期望值的偏离程度）

        （反映的取值与期望值的偏离程度）

 （综合反映了、与各自期望值的偏离程度）

        （反映平均偏离程度）

定义3.1 设二维随机变量，如果存在，则称

为协方差。

实质：随机变量函数的数学期望。

（1）离散型：；

（2）连续型：。

特别，当时，有

所以，方差是协方差的特例。协方差与方差之间有如下关系：

　　因此，。

协方差的性质：

（1）

（2）

（3）

（4）

（5）

（6）当与独立时，有。

证：（5）

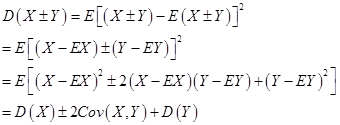
协方差存在的问题：

对于随机变量、、

令、、

与之间的关系，本来应该和与之间的关系相同，上式却扩大了倍。为了克服这个问题，用与的标准化随机变量来刻画与之间的关系，然后再计算协方差。

令：

则

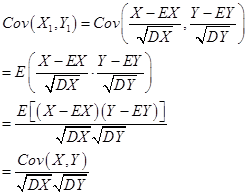
协方差作为描述X和Y相关程度的量，在同一物理量纲之下有一定的作用，但同样的两个量采用不同的量纲使它们的协方差在数值上表现出很大的差异。为此引入如下概念：标准化随机变量的协方差称为相关系数，记作

 （反映了与之间的（线性）关系）

例：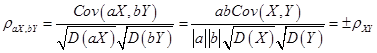

所以，克服了与本身量纲不同对与之间关系的影响。

相关系数的性质：

（1）；

（2），即与以概率1线性相关。

证明：

从以上性质可知，是衡量与之间线性相关程度的一个数字。

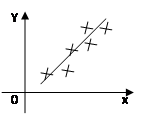
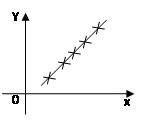
特别：当时，称与正线性相关；（）

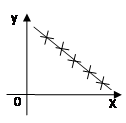
当时，称与负线性相关；（）

当时，与的这种线性相关程度将随着的减小而减弱。

当时，称与不线性相关。

图示： 

      

                                            

                         

                          

 、不相关与独立的关系：独立不相关，反之，不可以。

说明：    高度相关

    中度相关

    低度相关

    弱相关

若,则与独立。

例3.12 设的联合概率分布为                                       

	-1	0	1
0	0.1	0.1	0.1	0.3
1	0.3	0.1	0.3	0.7
	0.4	0.2	0.4	1

证明：与不相关，但与不独立。

证：

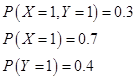
例3.13 设

，

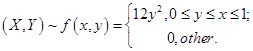求，并考察与是否相互独立。

解：

 

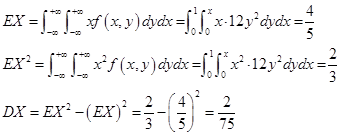
故

因为，所以与不独立。