第二节        概率分布 

概率分布（probability distribution）是随机变量x小于任何已知为实数x的事件的函数。

它用来描述随机变量值的概率规则。用不同概率分布描述不同类型的随机变量是概率论的基本概念之一。

概率分布是描述随机变量值概率的函数，有3种函数：

概率函数（probability function），用于描述离散随机变量采用每个可能值的概率。

概率密度函数（probability density function）函数，描述连续随机变量的密度取一定值。

概率分布函数（probability distribution function），用于描述随机变量取值小于或等于某个值的概率。也称为累积分布函数（cumulative distribution function）。

下面分别介绍离散性随机变量和连续性随机变量的概率分布。

1.离散性随机变量的概率分布

若随机变量X只可能取有限个或可列个值，称这种随机变量为离散型随机变量（discrete random variable）。

  （1）概率函数

  设X是某个离散性随机变量，其概率函数可表示为

                   （3-1）

  式中x为X的某个可能取值；表示X取值为x的概率。概率函数满足以下条件：

，

  为了直观起见，有时将X的分布律用如下表格表示：                       

X	x1	x2	…	xk	…
p	p1	p2	…	pk	…

    由概率的定义知，离散型随机变量X的概率分布具有以下两个性质：

    (1) pk ³ 0，(k = 1，2，…)       （非负性）

    (2)                     （归一性）

    这里当X取有限个值n时，记号为，当X取无限可列个值时，记号为。

    例3.1中X的分布率为                   

X	0	1	2	3
P	1/8	3/8	3/8	1/8

例3.6 独立地投掷2次骰子，所得点数之和为一随机变量，求该随机变量的概率函数。

解：每投一次骰子有6种可能结果，投2次的结果就有6×6＝36种组合，每种组合出现的概率为1/36。点数之和的可能取值为2到12，取值为2和12的组合只有1种，分别为两次都是1和两次都是6，因而它们的概率都是1/36；取其他值的组合都有至少2种，例如取值为3的组合有1+2和2+l，因而其概率为1/36+1/36＝2/36。于是，该随机变量的概率函数为：

            

式中和分别为第1次投掷和第2次所投掷的点数；为2次投掷点数之和为x的组合数。该概率函数的概率分布列为                                               

x	2	3	4	5	6	7	8	9	10	11	12
	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

           

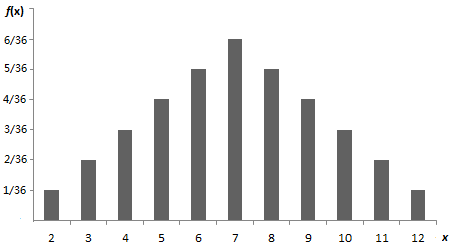
图3-1 投掷2次骰子所得点数之和的概率分布图

这个分布列也可用图3-1来表示： 

例3.7 投掷一次均质的骰子所得点数为一随机变量，求该随机变量的概率函数。

解：投掷一次骰子所得点数有6种可能，即点数为1到6，由于骰子是均质的，每种结果出现的概率是相同的，即都为1／6，因而该随机变量的概率函数为：

    

      该概率函数的概率分布列为：                           

x	1	2	3	4	5	6
	1/6	1/6	1/6	1/6	1/6	1/6

（2）概率分布函数

离散性随机变量X的概率分布函数为：

              （3-2）

例如对于例3.6中的随机变量，有

      （3）随机变量的期望（expectation）

随机变量的期望值（也称为数学期望值）是我们在一个实验中预期的随机变量的值，它是整体平均值。

对于概率函数为的离散性随机变量X，其期望为

               （3-3）

式中E为期望；为总体平均数以；x为X的某一可能取值，求和是对所有的。

对于例3.7，其随机变量的期望为：

期望的性质：设a是常量，X和Y是两个随机变量，则

           （X和Y彼此独立）

      随机变量函数的期望：设是离散性随机变量X的一个函数，则Y的期望为：

                （3-4）

式中为X的概率函数。

例如对于例3.7中的随机变量，求的期望。

（4）随机变量的方差（variance）

随机变量的方差是度量随机变量取值的变异程度的指标，它就是总体方差，其定义公式为

           （3-5）

式中var为方差，也常表示为；为总体平均数；N为总体含量；以为总体中的第i个观测值。注意此式与第2章介绍的样本方差计算公式的区别：分子中的离差是与总体平均数的离差而不是与样本平均数的离差，分母是N而不是N-1。此式还可进一步变化为：

                （3-6）

对于例3.7中的随机变量，其方差为：

      方差具有以下性质：

                 （是常量）   

       （X和Y彼此独立）

总体方差的平方根，即，称为总体标准差。

      2.连续性随机变量的概率分布

      除了离散的随机变量之外，还有一类重要的随机变量-连续随机变量，这个随机变量X可以取[a，b]或者所有值的间隔。例如灯的寿命，顾客购买东西的等待时间等等，因为这样的随机变量的所有可能值不能像离散的随机变量一个一个地排列，因此不能使用离散随机变量分布规律来描述其概率分布，理论和实践中常用的是随机变量概率分布的概率密度。

满足以下条件的函数称为连续性随机变量X的概率密度函数：

          （x是X的任一可能取值）

概率分布函数：

            （3-7）

连续性随机变量的期望：

               （3-8）

连续性随机变量的方差：

       （3-9）

       连续性随机变量的概率分布具有以下特点：

(1) 对于任意实数，有 

即连续型随机变量取某一实数值的概率为零。

       (2)

                    

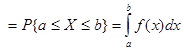
该式说明当计算连续型随机变量在某一区间上取值的概率时，区间端点对概率无影响。

   (3)                      

证法一：

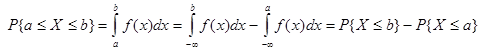
证法二：

    (4) 改变在有限个点的值，不影响的值。

    (5) 若在点x连续，由中值定理易知，落入微小区间的概率为

事实上

，

其中。

       例 3.8 设随机变量X具有概率密度

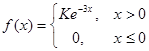
    (1) 试确定常数；

    (2) 求；

    (3) 求

    解： (1) 由于，即

  

          得.于是的概率密度

；

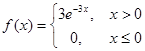    (2)  =;

    (3) ==