第二节 离散性测度 

一、标准差的意义

平均值作为样本的表示受样本数据中观察值变化的影响。如果观测值的变化很小，那么平均值代表性强，如果观测值变化很大，则平均值代表性弱。因此，通过平均数来统计描述数据的特征并不是全面的，应该引入一个统计量来指示数据中观测值的变化程度。

全距（极差）是最简单的统计量，用于表示数据中观测值的变化程度。当全距较大时，数据中每个观测值的变化程度较大，全距较小，数据中每个观测值的变化程度较小。然而，数据的全距仅使用最大值和最小值，并且数据中观测值的变化程度没有准确表达。当有大量数据并且您必须快速判断数据的可变性程度时，可以使用全距统计量。

为了准确地表示样本中每个观测值的变化程度，人们首先将平均值作为标准，以找出观测值与平均值之间的差异，即（），称为离均差。尽管离均差可以表示观察到的平均偏差的性质和范围，但差值的总和为零，即Σ（）=0。因此，数据中所有观测值的总偏差不能用离均差与Σ（）之差的和来表示。为了解决平均值和零之间的正，负和平均差之和的问题，我们可以首先找到平均差的绝对值，可先求离均差的绝对值并将各离均差绝对值之和除以观测值n求得平均绝对离差，即Σ||/n。尽管平均绝对偏差可以表示数据中观测值的变化程度，但平均绝对偏差包含绝对值符号，使用起来不方便，不用于统计。

我们也可以使用离均差平方和来解决离均差有正、有负，离均差之和为零的问题。先将各个离均差平方，即 ()2，再求离均差平方和，即Σ，简称平方和，记为SS；由于偏差的平方和随样本的大小而变化，平方和除以样本的大小用于消除样本大小的影响。为了使统计量是相应总体参数的无偏估计量，统计学证明求离均差平方和的平均数时，分母不需要样本含量n，且自由度为n-1，所以我们使用统计统计量Σ表示资料的变异程度。统计量Σ称为均方（mean square abbreviation，MS），也称为样本方差，记为S2，即

S2=                （2-9）

相应的总体参数叫总体方差，记为σ2。对于有限总体而言，σ2的计算公式为：

        σ2μ）2/N                  （2-10）

由于样本方差带有原观测单位的平方单位，在仅表示一个资料中各观测值的变异程度而不作其它分析时，常需要与平均数配合使用，这时应将平方单位还原，即应求出样本方差的平方根。统计学上把样本方差S2的平方根叫做样本标准差，记为S，即：

                     （2-11）

由于

                 

                 

                 

所以（3-11）式可改写为：

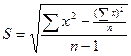                 （2-12）

相应的总体参数叫总体标准差，记为σ。对于有限总体而言，σ的计算公式为：

σ=                  （2-13）

在统计学中，常用样本标准差S估计总体标准差σ。

二、标准差的计算方法

（一）直接法  对于未分组或小样本资料，可直接利用（3-11）或（3-12）式来计算标准差。

例2.9 计算10只辽宁绒山羊产绒量：450、450、500、500、500、550、550、550、600、600、650（g）的标准差。

此例n=10，经计算得：Σx=5400，Σx2=2955000，代入（3-12）式得：

即10只辽宁绒山羊产绒量的标准差为65.828g。

（二）加权法  对于已制成次数分布表的大样本资料，可利用次数分布表，采用加权法计算标准差。计算公式为：

        （2-14）

式中，f为各组次数；x为各组的组中值；Σf = n为总次数。

例2.10 利用某纯系蛋鸡200枚蛋重资料的次数分布表（见表2-4）计算标准差。

将表3-4中的Σf、Σfx、Σfx2代入（3-14）式得：

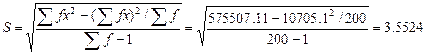（g）

即某纯系蛋鸡200枚蛋重的标准差为3.5524g。 

表2-4 某纯系蛋鸡200枚蛋重资料次数分布及标准差计算表                                                                        

组别	组中值（x）	次数（f）	fx	fx2
44.15—	45.0	3	135.0	6075.0
45.85—	46.7	6	280.2	13085.34
47.55—	48.4	16	774.4	37480.96
49.25—	50.1	22	1102.2	55220.22
50.95—	51.8	30	1554.0	80497.20
52.65—	53.5	44	2354.0	125939.00
54.35—	55.2	28	1545.0	85317.12
56.05—	56.9	30	1707.0	97128.30
57.75—	58.6	12	703.2	41207.52
59.45—	60.3	5	301.5	18180.45
61.15—	62.0	4	248.0	15376.00
合计	Σf=200        Σfx=10705.1 Σfx2=575507.11

三、标准差的特性

（一）标准差的大小，由各观测值的数据，如观测值之间的差异大，标准差也很大，反之则较小。

（二）计算标准偏差时，从每个观测值加上或减去一个常数，该值不变。

（三）当每个观测值乘以常数a或除以常数a时，标准差是原始标准差的a倍或1/a倍。

（四）在数据服从正态分布的情况下，数据中约68.26％的观测值在平均值的标准偏差（±S）内，大约95.43％的观测值在两倍平均值的标准偏差内（±2S），观测值的约99.73％为标准偏差（±3S）的三倍。换句话说，也就是说全距近似地等于6倍标准差，可用（）来粗略估计标准差。

一、变异系数

变异系数是衡量数据中每个观测值变化程度的另一个统计量。当对两个或多个数据进行比较时，如果测量单位与平均值相同，则可以直接与标准差进行比较。如果单位和平均数不同时，则不可能将方差与标准偏差进行比较，而是将标准偏差与平均数（相对值）进行比较。标准差与平均值的比值称为变异系数，即C·V。变异系数可以消除不同单位和平均数对两个或多个数据变异程度的影响。

变异系数的计算公式为：

                       （2-15）

例2.11 成年母猪的平均体重190kg，标准偏差10.5kg，成年母猪的平均体重196kg，标准差8.5kg，成年母猪的两个品种，那一个体重变异程度大。

此例观测值虽然都是体重，单位相同，但它们的平均数不相同，只能用变异系数来比较其变异程度的大小。

由于，长白成年母猪体重的变异系数：

大约克成年母猪体重的变异系数：

所以，长白成年母猪体重的变异程度大于大约克成年母猪。

注意，变异系数的大小，同时受平均数和标准差两个统计量的影响，因而在利用变异系数表示资料的变异程度时，最好将平均数和标准差也列出。 

二、统计图 

常用的统计图表是柱形图（bar chart），饼图（pie chart），折线图（linear chart），直方图（histogram）和折线图（broken-line chart）。图形选择取决于数据的性质，一般来说，测量数据使用直方图和折线图，计数数据，质量特征数据，半定量（等级）数据，常用的柱形图、线图或饼图。

（一）绘制统计图的基本要求

1.标题简洁，列在图下方。

2.垂直，水平两轴应有刻度，标明单位。

3.横轴从左到右，纵轴从下到上，数值从小到大，图形纵横比约为5：4或6:5。

4.图中需要不同颜色或线条来表示不同的内容，应该有一个图例说明。

（二）通用统计图表及其呈现方法

1.柱状图使用等宽的长方形，高度根据研究指标的指示属性类别或等级的数量或频率分布。如奶牛几种疾病的发病率，一些家畜对寄生虫的感染，不同公羊的油脂分布和汗液颜色等。如果只涉及一个指标，则使用单个柱状图，如果涉及两个或更多指标，则使用双柱状图。

绘制柱形图时，请注意以下几点：

（1）纵轴刻度从“0”开始，间隔相等，表示指示刻度的刻度和单位。

（2）横轴是柱状图的公共基线，每个条的内容应标出。条的宽度相等，间隔相同。间隔的宽度可以与条的宽度相同或一半。

（3）在绘制双柱形图时，将相同的属性类型，等级两个或两个以上的条形参数组合在一起绘制，各长条所表示的指标用图例说明，同一属性种类、等级的各长条间不留间隔。

例如，根据表2-5绘制的柱形图是单式的，见图2-1。根据表2-6绘制的柱形图是复式的，见图2-2。

                  表2-5 某品种鸡杂种二代冠形分离情况                       

冠    形	次数（f）	频率（%）
玫瑰冠	106	74.13
单   冠	37	25.87
合   计	143	100.00

 

表2-6 几种动物性食品的营养成分                                                                       

品别	百分比（%）
	蛋白质	脂肪	糖类	无机盐	水分	其它
牛奶	3.3	4.0	5.0	0.7	87.0	--
牛肉	19.2	9.2	--	1.0	62.1	8.5
鸡蛋	11.9	9.3	1.2	0.9	65.5	11.2
咸带鱼	15.5	3.7	1.8	10.0	29.0	40.0

图2-1 杂种二代鸡的冠形分离的次数分布图

图2-2  几种动物性食品的营养成分

2.饼图用于表示计数数据，质量性状数据或半定量（等级）数据的组成比。所谓组成比例是每个类别、等级的观察次数（次）和观察总次数（样本内容）的百分比。饼图的整个面积被认为是100％，并且根据每个类别和等级的组成比例将圆形区域分成若干部分，并且每个类别和等级的比例由扇区面积的大小表来表示。

绘制饼图时，请注意以下三点：

（1）饼图每个3.6°角度对应的风扇面积为1％。

（2）饼图的各部分按照数据顺序或大小的顺序顺时针排列，从时钟9点或12点开始。

（3）饼图的部分用线分隔，表简短的词和百分比。

例如根据表2-6中的数据用饼图绘出四种动物性食品的营养成分，见图2-3。

牛奶	牛肉	鸡蛋	咸带鱼

图2-3 四种动物性食品的营养成分

3.线图用于表示事物或现象随时间演变的情况。有两种折线图，单式和复式。

（1）单式线图表示物体或现象的动态。

例如，表2-7列出了猪场出生至六月龄的地方猪平均体重变化，据此可以将数据绘制成单一的线形图，以表示该猪场长白猪体重随月龄变化的情况，见图2-4。

表2-7  长白猪体重的变化（出生-6月龄）  单位：kg                               

月龄	出生	1	2	3	4	5	6
体重	2.0	13.5	27.5	43.0	61.2	83.8	118.5

  

图2-4  长白猪体重的变化（0-6月龄）

（2）复式线图  在同一图上表示两种或两种以上事物或现象的动态。这时可用实线“¾¾”，断线“------”，点线“····”，横点线“-•-•-•-”等来标志区别。

例如，长白猪、大约克、大白猪三个品种从出生到6月龄出栏平均体重的变化如表2-13所示，根据该资料绘制的复式线图，见图2-5。 

表2-13 三个品种猪体重的变化（出生—6月龄）  单位：kg                                                               

	出生	1	2	3	4	5	6
长白猪	2.0	13.5	27.5	43.0	61.2	83.8	118.5
大约克	1.8	12.0	24.5	38.0	53.6	72.3	104.5
大白猪	1.6	10.0	21.0	32.0	45.0	60.5	85.7

 

图2-5  三个品种猪体重的变化（0-6月龄）

4.直方图用直方图来表示数据，根据分布表的数量做出直方图来表示数据的分布情况。方法是在横轴上标记组限制，纵轴数（f），在各组上作出其高等于次数的矩形。

例如根据表2-1绘制的次数分布直方图，见图2-6。

5.折线图对于测量数据，我们也可以根据数字分配表制作折线图。方法是：标记组中位数在横轴上，纵轴上标记数量，横轴的每组数值，次数为纵坐标描点，用线段依次连接各点，即可得次数分布折线图。

例如根据表2-1绘制的次数分布折线图，见图2-7。

   图2-6  120头6月龄母猪体长次数分布直方图

图2-7  120头6月龄母猪体长次数分布折线图