第二章 资料的描述性统计分析
学习要求： 正确理解统计数据不同的计量尺度和类型，了解统计数据的来源有直接和间接两大类，掌握不同的统计调查方式和应用场合，掌握并学会应用统计数据的搜集方法，熟悉调查方案设计的内容。 |
数据整理基于调查目的和科学方法的运用，原始数据的审核，分组，总结，描述和归纳，使其组织化，便于对工作过程进行统计分析和推断。由于从调查或实验中收集的原始数据往往是杂乱无章的，只有通过统计整理才能发现内部关系和规律性，从而揭示事物的本质。数据整理是进一步统计分析的基础，本章首先介绍数据的分类，然后介绍不同类型的数据合成和表征。
数据的正确分类是数据整理的先决条件。在调查或实验中，从观测和测量获得的数据可以分为三类：测量数据、计数数据和分类数据，根据其不同的性质，可以分为：
一、测量数据
测量数据是指通过数量测量获得的数量性状数据，即通过测量工具直接获得的数量性状数据，如度、数量和尺度。这些数据的观察结果不一定是整数，任何有十进制数的数字都可以出现在两个相邻整数之间，小数位数由测量工具的精度决定，它们之间的变化是连续的。因此，测量数据也被称为连续变化数据。例如：羊毛产量、动物体重、牛奶生产。
二、计数数据
计数数据是指通过计数获得的数量性状数据。在这些数据中，其观察结果只能用整数表示。由于观测值只能用整数表示，观测值是不连续的，所以数据也称为离散变异性数据或不连续变异数据。例如：绵羊产仔数、鸡蛋产量。
三、分类数据
分类数据是指根据检查的性状或指标的顺序对观察单元的数量进行分组，然后对每组观察到的单位数进行计数。这种类型的信息具有数据数量的特征，以及差异的程度或数量。它通常是一个不连续的（离散的）变异数据。如果某种药物用于治疗某些畜禽疾病，其疗效可分为“无效”、“改善”、“有效”和“控制”四个等级，然后统计各级别的供试畜禽数。
第一节 位置测度
统计通常解决这样一类问题，即抽样一组数据样本x1，x2，…，xn，如何使用抽样样本来推断总体？在我们回答这个问题之前，我们将从样本的概述开始。它是一种通过样本中心或中心值来推断一批数据的度量形式的位置度量方法。常用的测度包括算术平均数（arithmeticmean）、中位数（median）、众数（mode）、几何平均数（geometricmean）及调和平均数（harmonicmean），现分别介绍如下。
一、算术平均数
（一）定义和计算：算术平均值是数据中观测值总和除以观测值的数量或平均值或平均值的商，记为
。算术平均值可以根据样本量和分组直接采用直接法或加权法计算。
1.直接法主要用于样本含量n≤30以下，未经分组资料平均数的计算。
设某一资料包含n个观测值：x1，x2，…，xn，则样本平均数可通过下式计算：
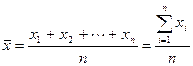（2-1）
其中，Σ为总和符号；
表示从第一个观测值x1累加到第n个观测值xn。当
在意义上已明确时，可简写为Σx，（2-1）式即可改写为：
例2.1某羊场测得10头基础母羊的体重分别为53.0、50.0、51.0、57.0、 56.0、51.0、48.0、46.0、62.0、51.0（kg），求其平均体重。
由于Σx=53.0+50.0+51.0+57.0+56.0+51.0+48.0+46.0+62.0+51.0=525，n=10代入（2-1）式得：
即10头种公牛平均体重为52.5 kg。
2.加权法 对于样本含量n≥30以上且已分组的资料，则可采用加权法计算平均数，计算公式为：
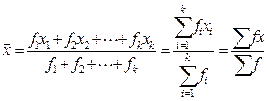（2-2）
式中：
—第i类个体在该指标上的取值；
—第i类的频数；
—类别数
例2.2 随机测量了某品种120头6月龄母猪的体长，经整理得到如下次数分布表。试利用加权法计算其平均数。
表2-1 120头6月龄母猪的体长分布表
组别 |
组中值（x） |
次数（f） |
80- |
84 |
2 |
88- |
92 |
10 |
96- |
100 |
29 |
104- |
108 |
28 |
112- |
116 |
20 |
120- |
124 |
15 |
128- |
132 |
13 |
136- |
140 |
3 |
利用（2-2）式得：
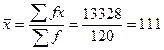
120头6月龄母猪的平均体长为111厘米。
应该注意的是，对于测量数据，用这种方法计算的平均值与2-1的平均值略有不同，因此是近似值。
在计算同一群体中平均样本平均数时，如果样本含量不相等，应使用加权方法。
例2.3 某牛群有黑白花奶牛1500头，平均体重为750 kg，而另一组牛有1200头黑白花奶牛，平均体重为725 kg，如果将二个牛群混合在一起，混合后的平均体重为多少？
在这种情况下，两个牛群中包含的牛的数量，并且获得了两个牛群重量的加权平均值，即
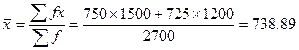
即两个牛群混合后平均体重为738.89 kg。
（二）算数平均数的基本性质
1.样本各观测值与平均数之差的和为零，即离均差之和等于零。
2.样本各观测值与平均数之差的平方和为最小，即离均差平方和为最小。
(xi-
)2<
(xi-a)2 （常数a≠）
二、中位数
数据中的所有观测数据从小到大依次排列，中间的观测值称为中位数，记为Md，当观测数为偶数时，中位数为两个观测值的中值的平均值，简称中位数。当获得的数据呈偏态分布时，中位数表示优于算术平均数。中位数计算方法根据数据是否分组而有所不同。
（一）未分组资料中位数的计算方法 对于未分组资料，先将各观测值由小到大依次排列。
1、当观测值个数n为奇数时，(n+1)/2位置的观测值，即x(n+1)/2为中位数；
Md=
2、当观测值个数为偶数时，n/2和（n/2+1）位置的两个观测值之和的1/2为中位数，即：
（2-4）
例2.4 观察得9只西农莎能奶山羊的妊娠天数为144、145、147、149、150、151、153、156、157，求其中位数。
此例n=9，为奇数，则：
Md=
=150（天）
即西农莎能奶山羊妊娠天数的中位数为150天。
例2.5 某犬场发生犬瘟热，观察得10只仔犬发现症状到死亡分别为7、8、8、9、11、12、12、13、14、14天，求其中位数。
此例n=10，为偶数，则：
即10只仔犬从发现症状到死亡天数的中位数为11.5天。
（二）已分组资料中位数的计算方法 若资料已分组，编制成次数分布表，则可利用次数分布表来计算中位数，其计算公式为：
（2-5）
式中：L-中位数所在组的下限；
i-组距；
f-中位数所在组的次数；
n-总次数；
c-小于中数所在组的累加次数。
例2.6 某奶牛场68头健康母牛从分娩到第一次发情间隔时间整理成次数分布表如表2-2所示，求中位数。
表2-2 68头母牛从分娩到第一次发情间隔时间次数分布表
间隔时间（d） |
头数（f） |
累加头数 |
12—26 |
1 |
1 |
27—41 |
2 |
3 |
42—56 |
13 |
16 |
57—71 |
20 |
36 |
72—86 |
16 |
52 |
87—101 |
12 |
64 |
102—116 |
2 |
66 |
≥117 |
2 |
68 |
由表2-2可见：i=15，n=68，因而中位数只能在累加头数为36所对应的“57—71”这一组，于是可确定L=57，f=20，C=16，代入公式（2—5）得：
即奶牛头胎分娩到第一次发情间隔时间的中位数为70.5天。
三、几何平均数
n个观测值相乘的平方根称为几何平均数，记为G。它主要用于畜牧业，水产养殖生产动态分析，动物疾病和药物滴度统计分析。如牲畜和家禽的增长率，水产养殖，抗体的效价，药物的效力以及动物疾病的潜伏期，用几何平均数比用算术平均数更能代表其平均水平。计算公式如下：
（2-6）
为了计算方便，可将各观测值取对数后相加除以n，得lgG，再求lgG的反对数，即得G值，即
（2-7）
例2.7 某波尔山羊群1997-2000年各年度的存栏数见表2-3，试求其年平均增长率。
表2-3 某波尔山羊群各年度存栏数与增长率
年度 |
存栏数（只） |
增长率（x） |
Lgx |
1997 |
140 |
— |
— |
1998 |
200 |
0.429 |
-0.368 |
1999 |
280 |
0.400 |
-0.398 |
2000 |
350 |
0.250 |
-0.602 |
Σlgx=-1.368 |
利用公式（2-7）求年平均增长率
G=
=lg-1[
（-0.368-0.398–0.602）]
=lg-1（-0.456）=0.3501
即年平均增长率为0.3501或35.01%。
四、众数
观察值的最大数量或一组组值中的观察次数或次数，称为众数，记为M0。如受精种蛋出雏天数次数分布中（表2-3所示），出现22次的次数最多，则众数为22天。另外，例如2.6所示，分配表中的次数57-71是最大的组，并组中值是64天，则该资料的众数为64天。
五、调和平均数
资料中各观测值倒数的算术平均数的倒数，称为调和平均数，记为H，即
（2-8）
调和平均值主要用于反映不同时期畜群的平均增长率或不同尺度下畜群的平均规模。
例2.8 不同世代的养牛规模为：0代200代，1代220头，2代210头，3代190头，4代210代头，试图找到其平均规模。
利用公式（2-8）求平均规模：
即保种群平均规模为208.33头。
对于同一资料，算术平均数>几何平均数>调和平均数。
上述五种平均数，最常用的是算术平均数。
