第三节 常用术语和基本概念
一、总体、个体和样本
一项研究所确定的全部研究对象被称为总体（population），也称为“统计总体”，其中一个研究单位称为个体（individual）或总体单元（unit）。通过某种方法从总体中提取的一些个体称为样本（sample）。例如，在对中国荷斯坦奶牛305d产奶量的研究中，中国荷斯坦奶牛305d产奶量的所有观察数据构成了中国荷斯坦奶牛首胎305d产奶量的总体。对200头中国荷斯坦奶牛第305d产奶量的观察，是中国荷斯坦奶牛305d产奶量的样本，其中有200个体。需要注意的是，总体定义是基于需要研究的问题，如果我们想研究中国荷斯坦奶牛体高，那么总体体高是由中国荷斯坦奶牛整体构成的；如果你想研究中国荷斯坦奶牛的体重，整个中国荷斯坦奶牛的总体规模，你也可以说，总体是由所有可能的随机变量值组成的。
按总体中所含个体的数目是否有限，总体可分为有限总体和无限总体。有限个体的整体称为有限个体，例如，中国荷斯坦奶牛在305d内产奶的总量仍然有限，尽管涉及的个体数量很大。总体为无限群体，其中包含无数个体，例如，在对生物统计理论的研究中，正态分布的整体，即t分布，包含了所有属于无限总体的实数。根据总体构成是否随时间变化，整体可以分为动态总体和固定总体，根据整体是否由存在对象构成，总体可以分为现实总体和假想总体。例如，如果要研究2010年东北长白猪，它是由2010年东北长白猪日增重组成的，这是一个有限的总体，固定的总体和现实的总体。如果在这个总体的定义中消除了时间的限制，那么整个总体是无限的（因为时间可以无限期地持续下去）和动态的总体。如果我们要看某种药物对某种疾病（有效或无效）的影响，我们将使用许多患病个体进行药效学实验，这些实验可能被视为来自假设总体的样本，这可能是所有个体对药物治疗的结果，而个体的数量可能是无限的，这不是现实，因为它不会为所有个体服用药物，但理论上我们可以将其用于所有个体。例如，几种饲料实验的饲养实际上并不存在于这类饲料的一般饲喂中，只是假设存在这种普遍性，实验被认为是假设种群的一个样本。在实际的统计分析中，我们遇到的大多数问题都是无限的，动态的和假设的。
样本中包含的个体数量称为样本容量或样本量（sample size）。中国荷斯坦奶牛305d产奶量的样本量为200。样本量通常记为n。通常n≤30的样本称为小样本，
样本称为大样本。
统计分析的目的是描述一般情况，推断不同总体之间的差异，但由于总体往往很大，往往是无限的，动态的和假设的，因此不可能为每个个体在总体中收集数据，通常的做法是以某种方式从总体中提取一些有代表性的个体（样本）。统计分析的基本任务是通过分析样本来推断总体。
二、变量、常数和观察值
变量（variable）是指其特征，其表现在不同的个体之间或不同群体之间的变异性，变量是对象特征的统计研究。它可以是定性的或定量的，并且定量变量是离散的或连续的。例如，身高，体重，产仔数，性别，发色，血型等，显然一些变量的表现可以用数值表示（如体重），而一些变量的表现要用文字描述（如头发的颜色），但有时为了方便计算，我们还可以用数值来描述变量的值，如红、白、黑三种头发颜色用1、2、3来表示。
常数（constant），也称为固定数字，是一个常量，具有不变值，与变量相反。
观察值（observation）是通过观察或测量变量的性能而获得的值，其有时被称为变数（variant）。许多指数的观察值具有直观和唯一的确定性。
三、参数、统计量和自由度
1.参数
参数（parameter）也称为参数变量，是一个变量。当我们考察当前的问题时，我们关注的是一些变量的变化以及它们之间的相互关系，其中一个变量称为自变量，另一个称为因变量。如果我们引入一个或一些其他变量来描述自变量和因变量的变化，则引入的变量不是当前问题必须研究的变量，我们称之为变量参数或参数。在统计中，常用参数是：总平均值（μ），总体标准偏差（σ），总方差（σ2）等。
2.常用统计量
统计量（Statistic）是统计理论中用于分析和验证数据的变量。样本的一个已知函数，其功能是汇集有关样本总体的信息; 它是数理统计中一个重要的基本概念。统计量仅取决于样本x1，x2，…，xn; 它不包含总体分布的任何未知统计参数。样本推断的总体（见统计推断）通常通过统计量来完成。例如，x1，x2，…，xn是从正态总体N（μ，1）（参见正态分布）绘制的简单随机样本，其中平均值（参见数学期望）μ是未知的，并且样本平均值被计算以便推断μ。可以证明，从某种意义上说，样本均值包含样本中μ的所有信息，因此可以很好地推断μ。样本均值仅取决于样本x1，x2，…，xn，是一个统计量。
（1）平均数
平均值（average）是反映变量分布集中性的特征值，是变量的典型或一般定量水平的代表值。最常用的是算术平均值。通过将n个数的总和除以n，商被称为算术平均值（arithmetic mean）。算术平均值的计算公式为：
（1-1）
n个观察值连乘积的n次方根就是几何平均数（geometric mean）。根据资料的条件不同，几何平均数分为加权和不加权之分。几何平均数的公式为：
（1-2）
调和平均值（harmonic mean）是平均数之一。但是，统计调和平均数与数学调和平均数不同。在数学中，调和平均值和算术平均值是独立的。计算结果不同，前者小于后者。因此，数学调和平均值被定义为数值倒数平均值的倒数。但是，统计加权调和平均值与加权算术平均值的加权算术平均值不同，它与算术平均值相关，不能单独成立。计算结果与加权算术平均值完全相等。它主要用于解决单位数（频率）不能被掌握，只有每个组的变量值和相应的标志总量的问题，但是需要获得数据的平均值。调和平均数的公式为：
（1-3）
加权平均数（weighted average）是不同权重数据的平均值，加权平均数是原始数据按照合理比例计算得出的，若n个数中，x1出现f1次，x2出现f2次，…，xn出现fn次，那么（x1f1 + x2f2+ ...+ xnfn）/（f1 + f2+ ... + fn）叫做x1，x2，…，xn的加权平均数。f1，f2，…，fn是x1，x2，…，xn的权。加权平均数的概念在描述性统计中具有重要意义，在其他数学领域具有较为普遍的形式。如果所有权重相同，则加权平均数与算术平均数相同。作为算术平均数的更一般化表示，加权平均数具有一些看似违反直觉的特性，如辛普森悖论，当人们试图探究这两个变量是否相关时，如入学率和性别，报酬和性别，等。辛普森悖论是在本研究的某些条件下有时会出现的现象。也就是说，即在分组比较中都占优势的一方，会在总评中反而是失势的一方。这个现象在20世纪初被讨论过，但直到1951年E.H.辛普森才在他的论文中被正式描述。然后他以他的名字命名了这个悖论。加权平均数的公式为：
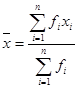（1-4）
说明：1）“权”的英文是weight，表示数据的重要程度。即数据的权能反映数据的相对“重要程度”。
2）平均数是加权平均数的一种特殊情况，即各项的权相等时，加权平均数就是算术平均数。
平方平均数（quadratic mean）或称均方根，是2次方的广义平均数的表达式，也可称为2次幂平均数。英文缩写为RMS（Root Mean Square）。平方平均数的公式为：
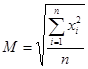（1-5）
此外，众数（mode）和中位数（median）也属于平均数。
平均数，中位数和众数之间的关系。平均数，中位数和众数是表征数据平均水平的统计数据，每种数据都有自己的特征。我们熟悉平均数，中位数描绘了一组中等水平的数据，一组数据中描绘的个体最多。平均值的明显优势之一是它可以利用数据的所有特征，并且可以更好地计算出来。另外，在数学中，平均值是使误差平方和达到最小的统计量，即使用平均数据，可以使二次损失最小。因此，平均值是数学中常用的统计量。但平均数也是不足的，因为它利用所有数据的信息，平均数对极端数据敏感。例如，在一个单位工资中，如果经理和副经理工资特别高，则会使单位所有成员的平均工资高，但实际上，不包括经理和副经理，其余的平均工资不是很高。在这一点上，中位数和众数可能是该单位所有人平均工资的更合理的统计数据。统计数据的中位数和众数都具有避免极端数据的能力，但缺点是数据反映的信息没有得到充分利用。由于每个统计量都有其自身的特点，因此我们需要根据实际问题选择合适的统计量。
当然，极端数据的发生并不一定在中位数，一般来说，有一种统计方法，有必要认为这种数据不是从总体上推导出来的，这样数据就被去掉了。例如，大家熟悉跳水比赛的比分，为什么要取消最高分数，最低分数呢，则认为这两点并非来自这个整体，不能代表裁判的口味，再求剩下数据的平均数。应该指出，我们现在处理的大部分数据是对称数据，数据符合或接近正态分布。在这一点上，均值（平均）、中位数和众数是相同的。
平均数，中位数和众数之间的差异。只有当数据分布偏态（不对称）时，才会出现平均数、中位数和众数的差异。所以，如果这是正态的，用哪个统计量都行。如果偏态特别严重，则可以使用中位数。除了需要描述统计的平均水平之外，统计众数还描绘了统计数据的波动。例如，平均值为5，其可以表示1、3、5、7、9，可能是4、4.5、5、5.5、6。也就是说，5所代表的不同组数据的波动情况是不一样的。如何描述数据的波动？自然的想法是使用最大值减去最小值，也就是找到一组极差（range）的数据。统计数据也具有方差、标准差和许多用于表征数据波动的统计特征。
（2）方差和标准差
方差（variance）是数据和平均值之差的平方的平均值。在概率和数学统计中，方差用于测量随机变量与其数学期望（即平均值）之间的偏差程度。在许多实际问题中，研究随机变量与平均值的偏差程度非常重要。方差的算术平方根称为标准偏差（标准偏差）。方差和标准差通过样本波动的大小来衡量，方差或标准偏差越大，样本数据的波动就越大。方差和标准差是衡量不连续趋势的最重要和最常用的指标。方差是每个变量值的平均值及其平均偏差的平方，这是计算数值数据离散度最重要的方法。标准差是方差的算术平方根，用S表示。相应的方差计算公式为：
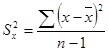（1-6）
标准偏差与方差之间的差异在于标准偏差与变量的计算单位相同，所以我们在分析它时更多使用标准偏差。相应的标准差计算公式为：
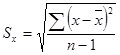（1-7）
其中，
是离均差平方和，简称平方和，记作SS；（n-1）称为自由度，记作df。
（3）变异系数
在概率论和统计学中，变异系数（coefficient of variation）也称为“离散系数”，是概率分布离差的归一化度量，它被定义为标准偏差与平均值的比值。标准差反映变量的平均变化程度，变量的相对变化可以用变异系数（C•V）表示。只有在均值不为零时才定义变异系数，一般适用于平均值大于0的情况。变异系数也称为标准偏差率或单位风险。变异系数的优势在于它不需要参考数据的平均值。变异系数是一个无量纲量，因此我们应该使用变异系数而不是标准差作为比较两组数据不同或平均值的参考。但变异系数也有其缺点。当平均值接近0时，小扰动会对变异系数产生显著影响，导致精度不足。另外，置信区间与平均值相似的概念不能通过变异系数来产生。
变异系数相应的计算公式为：
（1-8）
例如，种猪场的一头成年母猪平均体重190kg，标准偏差10.5kg，成年母猪平均体重196kg，标准偏差8.5kg，问成年母猪的两个品种，那个体重变化程度很大。虽然这个例子的观测值都是体重，单位是一样的，但它们的平均值并不相同，只能用变异系数来比较变异的程度。
由于，长白成年母猪体重的变异系数：
大约克成年母猪体重的变异系数：
所以，长白成年母猪体重的变异程度大于大约克成年母猪。
请注意，当使用变异系数来表示数据的可变性程度时，受平均值和标准偏差的两种统计量影响的变异系数的大小将优于平均值和标准差。
一些注意事项：
（1）对于每次观察，样本都是一组数字。但在不同的观察中，它需要不同的值。因此，整体而言，样本应该被视为一个随机变量，也有其自己的分布。样本的所有可能值的集合称为样本空间。
（2）样本的任何功能，只要它不包含未知参数，都可以称为统计量。例如
，
都是统计量，而
，
不是统计量，因为μ，σ是总体参数，一般是未知的。构建统计量的目的是集中我们关心的样本的信息，以便我们可以检查它，所以我们需要为不同的问题构建不同的统计量。
（3）为了使样本真实地反映整体特征，我们要求它具有代表性和随机性。也就是说，样本中的每个个体都必须具有与总体相同的分布，并且每个个体都是相互独立的。这样的样本被称为简单的随机样本。无放回采样的有限种群样本不是彼此独立的。但是，如果总数N很大并且样本含量n <0.1N，则它可以近似为简单的随机样本。
3.自由度
统计自由度（degree of freedom，df）是指样本中独立或自由变化的数据量，称为统计量的自由度。例如，对于一个统计量，如果变量X总共有n个值，如果它们受到k（k<n）个条件的限制，则df = n-k。
例如，在估计人口的平均数时，由于样本中n的个数相互独立，因此从中抽取的任何数字都不会影响其他数据，因此自由度是估计时的独立数据的数量总体参数，平均值根据n个独立数据估计，所以自由度为n。
估计总体的方差时，使用偏差的平方和。只要确定了n-1个平方数，就确定方差，因为如果在确定平均值之后n-1数的值是已知的，则确定第n个数的值。这里，平均值等于限制条件，因为添加了限制条件，估计总体方差的自由度是n-1。
其次，统计模型的自由度等于可以自由评估的自变量的数量。在回归方程中，如果需要估计P参数，则包含p-1参数（对应于截距的参数为常数1）。所以回归方程的自由度是p-1。
举一个形象的例子：如果你用刀切割柚子，在北极沿着经线切割3刀，6角的方向。这6个角度可以被认为是3对。6个角度的平均角度必须是60度。在三个角中，只有两个可以自由选择，一旦这两个数字确定了，第三个角度将被唯一确定。当总和已知时，分割角度的数量比自由分割的数量大1。
4.误差、准确性与精确性
（1）误差
误差（error）是数量与其值的观测值之间的差异；在存在统计误差的情况下，误差是不可避免的，也就是说，由于某些误差或由于某些不可控因素在测量，计算或观测数量中的影响而导致的与标准值或指定值的偏差数量。误差根据来源可分为随机误差（random error）和系统误差（systematic error）。误差又可分为绝对误差（absolute error）和相对误差（relative error）。
随机误差又称采样误差（sampling error），是由许多不可控制的内外部偶然因素引起的，如实验动物的初始条件、喂养条件、管理措施、实际测量仪器的差异、最小刻度低于读数估计误差等。这些因素不受人们控制，因此随机误差无法消除。
随机误差的大小可以用标准误来衡量，即平均数的标准差，其计算公式如下：
（1-9）
随机误差影响测试的准确性。统计测试误差是指随机误差。误差越小，测试的准确性越高。
系统误差也叫单侧误差（lopsided error），是由一些相对固定的因素引起的，如实验动物的种类、年龄、性别、病程、不同饲料种类、质量，数量等，管理措施差异很大，仪器不允许使用，标准试剂不予纠正药品的用量和种类不符合实验计划的要求。系统误差会影响测试的准确性，一般来说，只要实验认真完成，系统误差就很容易被克服。
绝对误差是测量值（单次测量或多次测量的平均值）与真值的差值。当测量结果大于真值时，误差是正值。绝对误差=测量值-真值。它等于置信区间的一半。当置信区间和置信区间的长度已知时，绝对误差在要求抽样量时起着重要作用。绝对误差
表示准确度的估计。
（1-10）
相对误差是绝对误差与真值的比值（通常用百分比表示），相对误差=绝对误差/真值。一般来说，相对误差可以更好地反映测量的可靠性。相对误差等于测量值减去实际差值除以真值乘以100％。例如，一名测量员使用相同的尺子来测量长度为1厘米和10厘米的物体，其测量的绝对误差明显相似，但相对误差的幅度高于后者，表明后一种测量是更可信。
系统误差是由一些固有因素（如测量方法的缺陷）引起的，从理论上可以通过某种方式来消除。例如天平的两臂的平衡应该是相等的长度，实际上可以不完全相等，相同质量的平衡重量应该是相同的，但实际上它们不能达到相同的效果。但随机误差顾名思义是随机产生的，不可预知的，它服从统计学上的所谓“正态分布”或“高斯分布”，在这个意义上，它并没有被消除，而是测量了对象的真实值是永远不知道的，只能通过一些平均的测量数据尽可能近似。偏差以同样的方式影响所有测量值，并将它们推向相同的方向。随机误差随着不同时间的测量而变化，有时会上升或下降。
用等式可以表达，随机误差中可能存在的结果为：
单独测量值 = 精确值 + 随机误差
而系统误差中，则结果为：
单独测量值 = 精确值 + 偏度 + 随机误差
误差的分布具有以下性质：误差的绝对值有一定的限制，绝对值较小的误差远大于绝对值的误差大，正负误差的个数相似。
还有一个误差是人为的，比如操作错误，遗漏或丢失数据，如原则上不允许产生错误，一旦发现错误，应将相关数据排除在外，不在误差范围之内。
（2）准确性与精确性
准确性（accuracy）也称为准确度，指的是观察值或估计值接近真值。如果事实是真的，则观察值是x或预测值û，μ与x（或û）差异的绝对大小反映了准确度。精确性（precision）也称为精度，它是对同一对象的重复观测值或估计值的接近度。如果观测值彼此接近，即任意两个观测值xi、xj，则差值的绝对值xi—xj很小，观测值准确，反之则较低。调查或测试的准确性和准确性称为正确性。准确性与数据中有效数字的数量有关。有些重复的观察值在有效数字较少时非常准确，例如只有整数，但当增加有效数字的数量时，会显示差异。例如，仔猪体重的两项指标分别是15.6kg和16.4kg，两者之间的差异为0.8kg，但如果只采用整数（四舍五入），则没有差异。有效位数除了人为的权衡之外，还与测量仪器的准确度有关，如普通天平，只能说是单位重量的克数，克下面的数不敏感，以及电子天平可以称为0.001g或0.0001g的重量。在生物学研究中，有一个共同的简单规则，即30-300规则，它是数据之间差异的最小单位，最小值和最大值之差应在30-300单位内。
