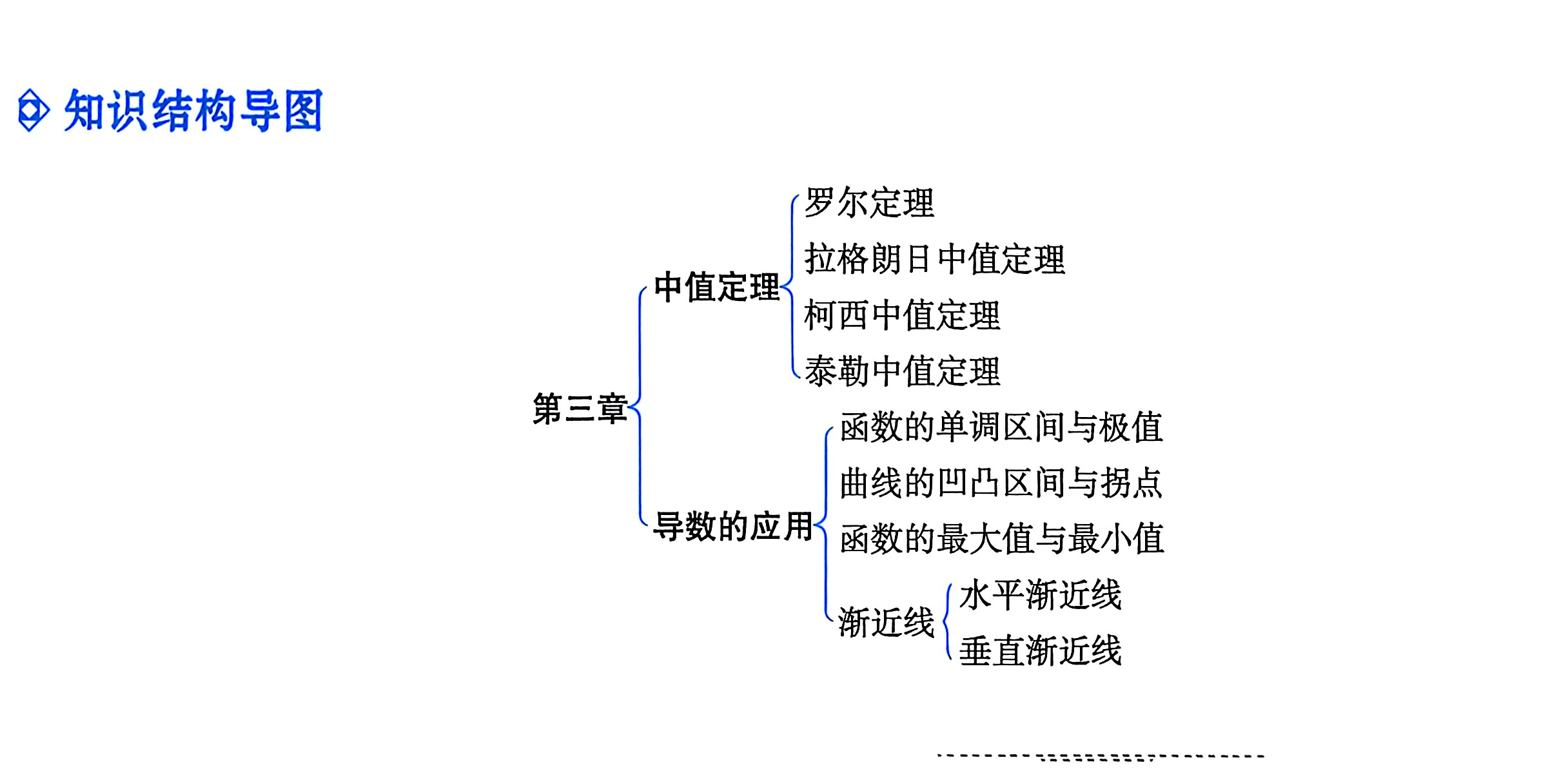
米歇尔·罗尔(Michel Rolle,1652年4月21日—1719年11月8日)是法国著名数学家,主要在代数领域有杰出贡献。
生平
罗尔出生于法国昂贝尔特的一个小店主家庭,只接受过初等教育。他年轻时生活贫困,靠担任公证人和律师抄录员的微薄收入维持生计。罗尔利用业余时间刻苦自学代数和丢番图的著作,并取得了显著成果。1682年,他因解决数学家奥扎南提出的一个数论难题而声名鹊起,此后生活逐渐好转,先后担任初等数学教师和陆军部行政官员。1685年,罗尔进入法国科学院,1699年成为科学院的固定成员,直到1719年在巴黎因中风去世。
数学成就
代数领域:罗尔在代数方面成就卓越,专长于丢番图方程的研究。1690年,他出版了《代数学讲义》,系统地解决了丢番图的线性方程问题,并掌握了方程组的消元法。他还提出了“级联”法则来分离代数方程的根。
罗尔定理:1691年,罗尔在论文《任意次方程的一个解法的证明》中提出了一个重要结论:在多项式方程的两个相邻实根之间,其导数方程至少有一个根。虽然罗尔当时并未使用导数的概念和符号,但这一结论后来被推广为微积分中的罗尔定理。
数学符号:罗尔在《代数学讲义》中设计了表示 x的 n次方根的标准符号,这一符号被广泛接受并沿用至今。
对微积分的态度
罗尔所处的时代正值牛顿和莱布尼茨创立微积分不久,由于微积分当时存在逻辑上的缺陷,罗尔曾对其表示怀疑,甚至称其为“巧妙的谬论的汇集”。1700年,他与瓦里格农等人在法国科学院就无穷小方法展开激烈争论。不过,罗尔后来逐渐认识到微积分的价值,并在1706年承认了其重要性。
罗尔的贡献在数学史上具有重要意义,尤其是罗尔定理,为微积分的发展奠定了基础。
约瑟夫·路易·拉格朗日(Joseph-Louis Lagrange,1736年1月25日—1813年4月10日)是法国历史上著名的数学家、物理学家和天文学家,他在数学的许多领域都取得了极为重要的成就,是18世纪最重要的数学家之一。
生平
早年经历
拉格朗日出生于意大利都灵的一个富裕家庭,他的父亲是一位法国军官。拉格朗日最初学习法律,但很快对数学产生了浓厚的兴趣。他在16岁时开始学习数学,18岁时已经对牛顿的微积分产生了浓厚的兴趣,并通过自学掌握了当时最先进的数学知识。
学术生涯
1754年,拉格朗日开始在都灵皇家炮兵学校担任数学教授。1756年,他被选为柏林科学院的外籍院士。1766年,他应欧拉的推荐,接替欧拉成为柏林科学院的数学部主任。在柏林期间,拉格朗日完成了许多重要的数学和天文学研究。
1787年,拉格朗日移居巴黎,成为法国科学院的院士。在法国大革命期间,他积极参与了法国的度量衡改革工作,推动了十进制的普及。1797年,拉格朗日被任命为巴黎综合理工学院的教授,直到1813年去世。
数学成就
分析力学
拉格朗日最著名的贡献之一是他在分析力学领域的开创性工作。他在1788年出版的《分析力学》一书中,将牛顿的力学理论用分析的方法重新表述,提出了拉格朗日方程。拉格朗日方程是经典力学的基础方程之一,它通过引入广义坐标和广义力,将力学问题转化为求解一组微分方程,极大地简化了力学问题的求解过程。
变分法
拉格朗是日变分法的奠基人之一。他在1760年左右发展了欧拉的变分法理论,提出了拉格朗日乘数法。拉格朗日乘数法是一种求解条件极值问题的通用方法,广泛应用于数学、物理和工程领域。
数论
拉格朗日在数论方面也有重要贡献。他证明了费马关于多边形数的猜想,即每一个正整数都可以表示为最多四个平方数的和。他还研究了二次型的理论,提出了拉格朗日四平方和定理。
微积分
拉格朗日在微积分方面也有许多贡献。他提出了泰勒级数的余项公式,即拉格朗日余项公式。他还研究了函数的极值问题,提出了拉格朗日中值定理,这是微积分中的一个重要定理。
天文学
拉格朗日在天文学方面也有重要贡献。他研究了三体问题,提出了拉格朗日点的概念。拉格朗日点是指在两个天体引力作用下,第三个天体可以保持相对静止的点。这一理论在现代航天工程中具有重要应用。
对后世的影响
拉格朗日的数学成就对后世产生了深远的影响。他的《分析力学》成为经典力学的标准教材,他的变分法理论为现代数学和物理学的发展奠定了基础。他的数论和微积分研究成果也被广泛应用于各个领域。拉格朗日的数学思想和方法至今仍然是数学研究的重要工具。
拉格朗日的成就使他成为18世纪最重要的数学家之一,他的工作不仅推动了数学的发展,也为物理学、天文学和工程学的进步做出了重要贡献。
奥古斯丁·路易·柯西(Augustin-Louis Cauchy,1789年8月21日—1857年5月23日)是法国著名的数学家、物理学家和工程师,他在数学的多个领域都有开创性的贡献,是19世纪最重要的数学家之一,尤其在分析学、复变函数、数论和数学物理等领域成就斐然。
生平
早年经历
柯西出生于法国巴黎,他的父亲是一位政府官员。柯西从小就对数学表现出浓厚的兴趣,1805年,他考入巴黎综合理工学院,师从拉格朗日和拉普拉斯等数学大师。1807年,他进入国立桥梁公路学校学习土木工程,毕业后成为一名工程师。
学术生涯
柯西在工程工作期间,仍然坚持数学研究。1814年,他发表了第一篇数学论文,此后他的研究逐渐受到数学界的关注。1816年,他被任命为巴黎综合理工学院的数学教授,随后又在法兰西学院和巴黎大学担任教职。
柯西在学术生涯中一直致力于数学分析的严格化。他强调数学证明的严谨性和逻辑性,推动了分析学从直观和几何方法向严格代数和逻辑方法的转变。他的工作为现代数学分析奠定了基础。
晚年
柯西晚年继续从事数学研究,他在复变函数、数论和数学物理等领域都有重要成果。1857年,柯西因病去世,享年67岁。
数学成就
分析学
柯西是现代分析学的奠基人之一。他在1821年出版的《分析教程》中,首次系统地引入了极限、连续性、导数和积分的严格定义。他提出了极限的“ε-δ”定义,这一定义至今仍然是数学分析的核心内容。柯西还建立了级数理论,提出了级数收敛的柯西准则。
复变函数
柯西在复变函数领域做出了开创性的贡献。他在1825年提出了复变函数的积分定理,即柯西积分定理。他还发现了柯西积分公式和留数定理,这些成果奠定了复变函数理论的基础。柯西的复变函数理论为后来的数学家如黎曼、魏尔斯特拉斯等人的研究提供了重要工具。
数论
柯西在数论方面也有重要贡献。他研究了二次型的理论,提出了柯西-施瓦茨不等式。他还研究了素数分布问题,提出了许多重要的猜想和定理。
数学物理
柯西在数学物理领域也有许多成果。他在弹性力学中提出了柯西应力张量的概念,这一概念至今仍然是固体力学的基础。他还研究了波动方程和热传导方程,提出了许多重要的解法和理论。
对后世的影响
柯西的数学成就对后世产生了深远的影响。他的分析学理论为现代数学分析奠定了基础,他的复变函数理论成为数学的一个重要分支。他的数论和数学物理研究成果也被广泛应用于各个领域。柯西的数学思想和方法至今仍然是数学研究的重要工具。
柯西的贡献使他成为19世纪最重要的数学家之一,他的工作不仅推动了数学的发展,也为物理学、工程学和计算机科学的进步做出了重要贡献。
洛必达
L’Hospital
(1661~1704)
洛必达(L’Hospital)是法国数学家,1661年生于巴黎,1704年2月2日卒于巴黎。
洛必达生于法国贵族家庭,他拥有圣梅特候爵,昂特尔芒伯爵称号。青年时期一度任骑兵军官,因眼睛近视自行告退,转向从事学术研究。
洛必达很早即显示出其数学的才华,15岁时就解决了帕斯卡所进出的一个摆线难题。
洛必达是莱布尼兹微积分的忠实信徒,并且是约翰.伯努利的高足,成功地解答过约。伯努利提出的“最速降线”问题。他是法国科学院院士。
洛必达的最大功绩是撰写了世界上第一本系统的微积分教程--------《用于理解曲线的无穷小分析》。这部著作出版于1696年,后来多次修订再版,为在欧洲大陆,特别是在法国普及微积分起了重要作用。这本书追随欧几里得和阿基米德古典范例,以定义和公理为出发点,同时得益于他的老师约翰.伯努利的著作,其经过是这样的:约翰.伯努利在1691-1692年间写了两篇关于微积分的短论,但未发表。不久以后,他答应为年轻的洛必达讲授微积分,定期领取薪金。作为答谢。他把自己的数学发现传授给洛必达,并允许他随时利用。于是洛必达根据约翰.伯努利的传授和未发表的论著以及自己的学习心得,撰写了该书。
洛必达曾计划出版一本关于积分学的书,但在得悉莱布尼兹也打算撰写这样一本书时,就放弃了自己的计划。他还写过一本关于圆锥曲线的书——《圆锥曲线分析论》。此书在他逝世之后16年才出版。
洛必达豁达大度,气宇不凡。由于他与当时欧洲各国主要数学家都有交往。从而成为全欧洲传播微积分的著名人物。