各学科研究者都在自己的领域内研究着网络（数学、社会学、经济学、生物学、计算机科学等等）。

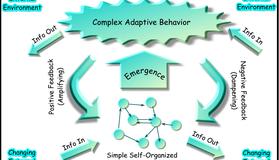
近20年，网络科学飞速发展起来，成为科学研究的新热点。

网络科学的目标：

• 寻找所有网络的共性之处

• 解释为何有这些共性

• 提炼出描述网络的结构、演化和动力学的基本理论。

‍（可能的）网络基本属性‍

小世界属性(Small world property)

长尾度分布(Long-tailed degree distribution)

特例: 非标度结构(Scale-free structure )

群聚和社团结构(Clustering and community structure)

对随机的节点失效具有鲁棒性(Robustness to random node failure)

对针对hub节点的攻击具有脆弱性(Vulnerability to targeted hub attacks)

对级联失效具有脆弱性(Vulnerability to cascading failures )

一些术语

点与边

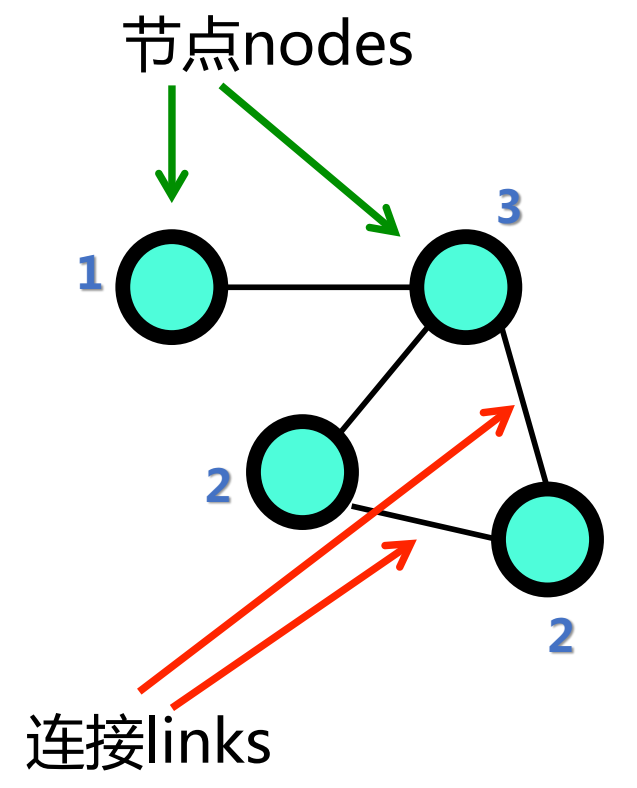
复杂网络使用了很多图论的工具，很多术语也来源于图论。

节点：Node(或 Vertex），连接（连结、边、向量）：Link（Edge，Vector）

节点的度（Degree）：与节点相连的边的数量，当节点间的连接是唯一的时候，也可以理解为与节点有联系的其他节点的数量。图中的蓝色数字就是节点的度。

连接可以是无向（undirected）的，也可以是有向（directed）的。在一个有向网络里，节点的度可以分为入度(in-degree)和出度(out-degree)。

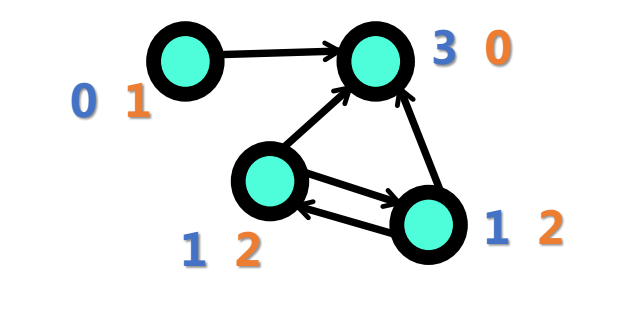
度分布

‍网络的度分布（Degree distribution of a network）为网络中节点的度的概率分布或频率分布(统称分布)。‍

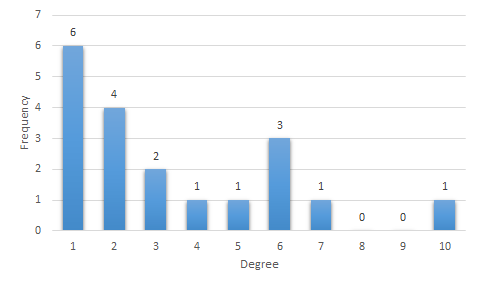
第一幅图所示网络的度分布：

度分布的实例：

我们参考书的作者M. Mitchell把她的社会关系按照网络的规则画了出来，里面的节点是人，如果两人认识，则认为两人之间有连结。

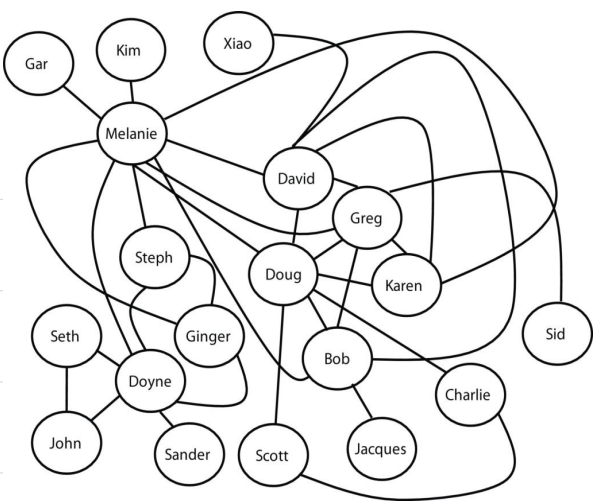
我们数数每个人有几个朋友，然后做出频度图。

网络中的距离(Distance)与路径(Paths)

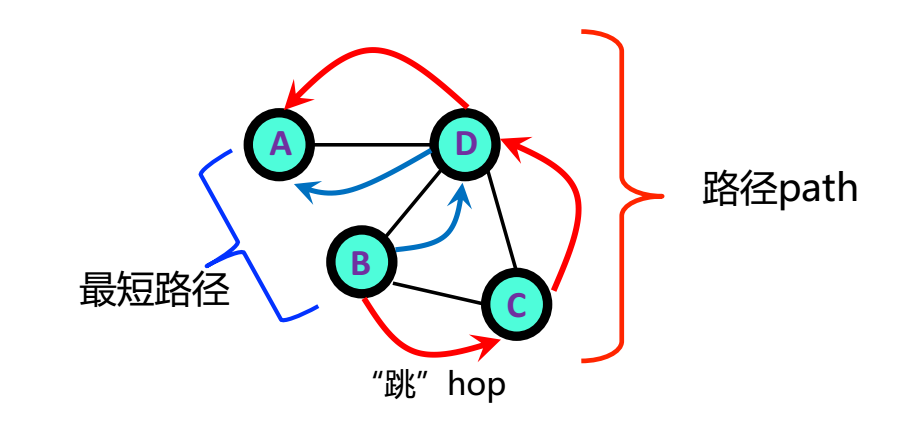
网络（图）是抽象的，连结（边）的长度没有实际意义，一条边的长度就是一“跳”（hop），路径上有几条边，长度就是几跳。

两个节点间的距离L就是两个节点间最短路径的跳数。

        

对于整个网络来说，，我们称其为“直径”。也就是说，一个网络的直径等于网络内所有节点两两之间距离的平均值。

聚集（Clustering）

Clustering: 你的朋友之间也是朋友的程度。

对于节点v，设其聚集系数为其邻居中互相之间又是朋友占邻居总数的比例。

即对于节点v来说有个邻居，那么在理论上最多可能有 “对”邻居，

则是邻居之间实际存在连接的数量与理论最大值之间的比值。

网络的聚集系数(Clustering coefficient)是所有节点聚集系数的算数平均值。

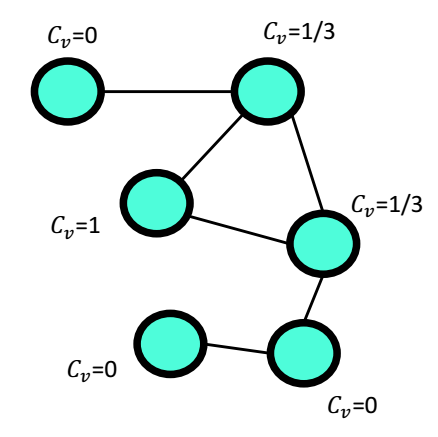
整个网络的聚集系数