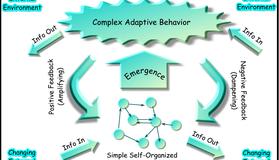
Self-Organization and Cooperation in Economics

‍Traditional economics‍

Assumptions:

• Perfectly rational self-interested agents

• Each has complete knowledge of others’strategies

• Each can do deductive reasoning

Result:“ Efficiency”（Best possible situation for all）

Can make predictions with analytic (mathematical) models, assuming “equilibrium” dynamics.

‍“Complexity” economics‍

Assumptions:

• Self-interested agents with bounded rationality

• Limited knowledge of others’strategies

• Each does primarily inductive reasoning

• Agents adapt over time to ever-changing environment

Analytic models often not possible; equilibria are never reached; often need agent-based models with ability to adapt.

El Farol Problem

How can all the people “cooperate” without communicating and without rational deductive reasoning?

• 每周四晚上会有爱尔兰音乐的现场演奏（大家都喜欢）

• 60人刚刚好

• 100个人想去，但是只有当他们知道要去酒吧的人少于60个才真的想去

• 人们没有事先联络

• 每个人知道的信息都是上M个周四分别有多少人去了酒吧

• 例如，M = 3, 人们得到的信息是上周四去了20个人，大上周四去了76人，三周前的周四去了35人

每个人要做出的决策是：这周四我该去吗？

Netlogo 模型库 -> social science ->El Farol

• 每个人有N个策略，每个策略都是通过历史数据预测本周四有多少人会去。

•  每个人都可能有不同的策略组

• 例如，如果 N = 3, 那么你的策略组可能是：

• Strategy 1: = 上周人数

• Strategy 2: = 100-上周人数

• Strategy 3: = 0.2 * last week + 0.1 * two weeks ago

• 为了做出决策，你要决定那个策略是“当下最好”的。

• 使用选出的策略预测本周四将会去的人数，如果超过60，则决定不去，否则就去。

• 所有人独立的同时进行预测，并且没有沟通。

El Farol 模型的意义

• 有限理性“ bounded rationality”

• 不完全信息 limited knowledge

• 包含适应性Includes adaptation (inductive learning from experience)

‍El Farol模型显示了自组织合作和效率是可以在没有完美理性、完全信息和演绎推理的形况下存在。‍