囚徒困境模型是社会科学研究中最著名和最有影响力的理想模型之一。
囚徒困境实在1950年代被两个数学博弈论学家M. Flood和M. Drescher发明用来研究敌对国家间的合作行为。
如果应用于美苏核军备竞赛,那么双方都会选择发展核武器,而实际上最好的结果却是双方都不发展核武器。 应用于全球变暖问题谈判也是同样……这就是囚徒困境悖论。
“The pursuit of self-interest by each leads to a poor outcome for all. “
by Robert Axelrod
经济学家哈丁(Garret Hardin)用“公地悲剧” (Tragedy of the Commons)来描述这一现象。
囚徒困境(The Prisoner's Dilemma)问题
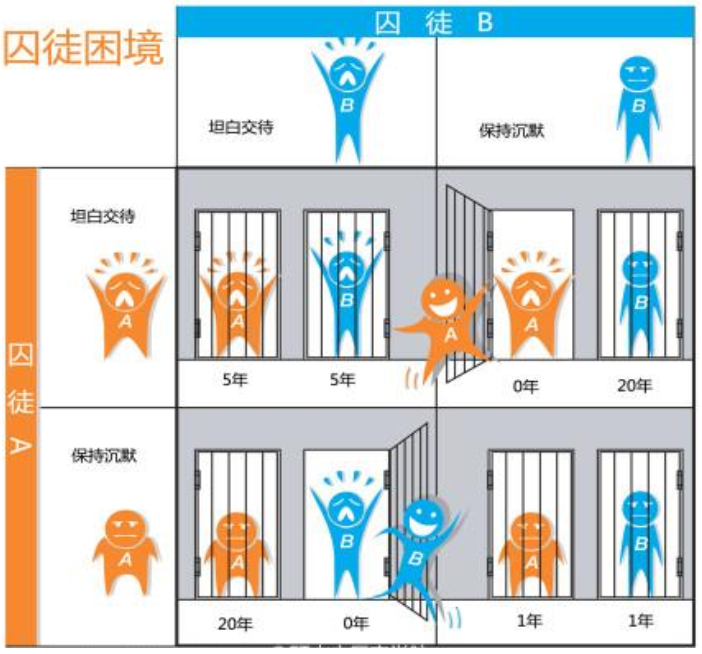
两个罪犯A和B是同伙,被逮捕后分开审讯。
二人不知道对方情况,要独立做出是否招供的决定。
招供并指认同伙,使同伙获刑的人会被释放。
如果互相指认,两人都不会被释放但会获得减刑(5年)。
拒不招供,如果被同伙招供指认则重判(20年);如果同伙也没有招供,则因为缺少人证只能轻判(1年)。
如果你是其中的一个,你会如何决策?
囚徒困境问题的分析
首先要把问题量化和通用化。
对于囚徒困境问题,坦白交代相当于不与同伙合作,而保持沉默则相当于合作。
对于关押的时间,可以量化为效用:根据常理,被判刑年数越少效用越高。设定效用最高为10,最低为0。则判处20年、 5年、1年和释放对应的效用为0,5,9,10。
之后,我们就可以使用一种叫做支付矩阵(payoff matrix)的工具分析,事实上,支付矩阵也是对博弈论问题分析的通用工具。
| B | ||
| A | 不合作 | 合作 |
| 不合作 | 5,5 | 10,0 |
| 合作 | 0,10 | 9,9 |
通过这个矩阵我们可以得出,对于单个罪犯来说,当对方合作与不合作的概率各占50%的时候:
选择不合作得到的效用是 50% × 5 + 50% × 10 = 7.5
选择合作能得到的效用是 50% × 0 + 50% × 9 = 4.5
那么结果显而易见,两名罪犯都会选择不合作,也就是招供并指认对方。
但是从犯罪团伙这个群体的角度来看,只有两名罪犯合作,也就是都不招供,群体才能获得最大的效用:9 + 9 = 18,这时每个罪犯的效用都是9;而按照罪犯们自己效用做化做出的决定选择不合作,那么每个罪犯的效用仅有5,群体的效用也只有10,均低于选择合作。
囚徒困境中的“困境”就是:群体里的每个个体使自身效用最大化的理性行为,反而无法达成自己的最大效用,也无法使群体达成最大效用。
有什么办法能够实现合作呢?如果两名罪犯学过我们这门课,能够使用支付矩阵分析问题,是不是就可以实现合作?如果罪犯在做决定之前能够充分沟通,是不是能够实现合作?
真实的囚徒困境
腐国人搞了个挺无聊的电视娱乐节目叫“Golden Balls”,节目内容无非是参与挑战赢大奖之类,但是这个节目有一个很有趣的环节"Split or Steal",在这个环节里,两名参与者会共同决定如何分配十几万英镑的高额奖金。
这个环节的名字和吸引人之处来源于其简单的规则,两名参与者各自选择“split”(平分)或者“steal”(偷取),有以下几种可能:
如果两人都选择split,则两人平分奖金;
如果一人选择split,一人选择steal,则选择steal的人获得全部奖金,另一个人一分钱也拿不到;
如果两人都选择steal,则都空手回家。
也就是说,两人合作则平分奖金;一个合作一人背叛,则叛徒占便宜好人吃亏;要是俩都是坏人那就一起遭报应吧。
这不就是囚徒困境真人版吗?
根据这个规则,咱们可以画出支付矩阵:
| Split | Steal | |||
| Split | 50% | 50% | 0 | 100% |
| Steal | 100% | 0 | 0 | 0 |
分析结果不用说了,从个体角度出发选择Steal效用最大,但是最终结果也可想而知。
如何才能产生合作呢?我们上面提到了是不是可以通过沟通实现合作。
这个节目也允许两名参与者在决定之前充分沟通,而且是当着众多观众的面充分沟通,于是多少人编出好听的故事,承诺自己会选择split。诸如什么父母双亡,从小接受无数人帮助才到了今天,因此要把感恩之心传递下去;什么曾经奇迹般地从车祸中幸存,感到自己被老天保佑,因此愿意从此做个好人;什么自己孩子刚刚出生,希望自己能为孩子做一个榜样;什么自己是个虔诚的信仰者,不会做出违背主的旨意的事情。
但结局呢?我们找一集看看这个节目的日常......
没有字幕,但是这里有双方和主持人的对话文字版以及一些分析。这节目完美的展示了人性的多(chǒu)样(è),看来就算有充分的沟通也没个卵用。
眼看人类就要败在囚徒困境这个问题前面,直到一个叫Nick Corrigan的人出现......
Nick一上来就向对方保证他一定选Steal:
当山峰没有棱角的时候
当河水不再流
当时间停住日月不分
天地万物化为虚有
我还是会选Steal,会选Steal......(领会精神)
不过Nick表示当他选Steal得到全部奖金后,他会分给对面的小哥一半的钱,只要对面的小哥选Split让他得逞,所以对面小哥你一定要选Split啊。
主持人当即提醒对面小哥,节目结束之后的事我们可不管。对面小哥亲切的称呼Nick为SB以表达他此时此刻的激动心情。在场的吃瓜群众们也不约而同的引用了中国古代杰出的政治家、军事家、外交家、散文家、书法家、发明家、文学家诸葛孔明先生的名句一吐为快:

场面一度失控,直到最后的时刻到来:

对面小哥选了Split
Nick也选择了Split
Nick把支付矩阵砍掉了一半,然后给了对方一个规则之外的许诺,使对方只能选择合作,而自己实际上选择的也是合作,从而在规则以内实现了合作,解决了囚徒困境的问题。详细的分析见这里。
囚徒困境问题的扩展
Nick在Golden Balls中的策略解决的实际是一次囚徒困境博弈,如果囚徒困境博弈是反复多次的,那么恐怕他的招数就不灵了。

The Evolution of Cooperation, 1984
The Complexity of Cooperation, 1997
“My main motivation for learning about effective strategies was to find out how cooperation could be promoted in international politics, especially between the East and the West during the Cold War.”
核心问题是:
如何在没有中央集权的前提下,什么样的条件能够让合作在利己主义者中间涌现出来?
Robert Axelrod
贯序博弈下,合作行为会不会产生?如何产生?
1980年代,Axelrod组织了两次锦标赛(Axelrod’s Prisoner’s Dilemma Tournaments),邀请了很多科学家和数学家参与提交策略。
策略被写成计算机程序,然后采用大循环方式一一进行贯序博弈。有些策略非常复杂,例如对不同对手创建复杂的预测模型。
但是两次锦标赛的获胜者都是最简单的策略:针锋相对(TIT FOR TAT ),submitted by Anatole Rapoport.
TIT FOR TAT: 第一次合作,随后采用对手上一次的策略。
Axelrod认为TIT FOR TAT策略能够取胜是因为其具有下面四个特点:
Be Nice (never be first to defect)
Be Forgiving (be willing to cooperate if cooperation is offered)
Be Retaliatory (be willing to defect if others defect against you)
Be Clear (be transparent about what your strategy is make it easy to infer)
Axelrod在后续的研究中加入了社会规范
规范:在其背叛行为被其他人发现时的社会谴责(负分)。
个体的每次背叛,都有一定概率被其他个体发现。
个体除了具有决策合作还是背叛的策略,还有发现背叛行为时是否进行惩罚的策略。
每次博弈后通过演化产生下一代策略。
结果表明仅仅规范并不能保证正义的产生。
随后又加入了元规范(metanorms),引入执法者来惩罚非执法者。如果周围有执法者,非执法者就会演化的更倾向于惩罚背叛行为,而背叛者也会演化的更愿意合作。
Martin Nowak加入了空间结构
类似于元胞自动机的元胞,个体与周围的邻居进行博弈。
个体策略非常简单,得分是与8个邻居博弈得分的和,然后选择八个邻居和自己之中得分最高的策略为自己下一轮的策略。
空间结构能够产生类似混沌和震荡的效果。
空间结构的引入能使合作者背叛者共存,而不需要引入规范或者元规范。
结论是空间相邻关系的存在会促进合作。