自然界的同步实例

萤火虫发光（某些特定种类的萤火虫）

鸣虫和蛙类的鸣叫

（周期）蝉的发育和孵化

神经元放电

心肌细胞跳动

生物同步的原因有很多假说：

• 让雄性的位置更明显，更易被雌性发现

• 让小群的雄性显得更大，更容易吸引雌性

• 减少“噪声”，雄性能在发光的间歇更好的识别黑暗中的异性

这些假说可能都是对的…… 

如何实现同步？

以萤火虫为例，假定:  

• 没有领导者   

• 每个萤火虫只能看到附近的发光

萤火虫实际是天然的振荡器，以一次一秒的频率发光。作用于神经元的刺激累积达到阈值，则开始发光。如果萤火虫看到邻居发光，她将调整自己的发光循环

最后的结果就是同步发光（耦合振荡器）

Netlogo的模型库里，在Biology下有Fireflies模型。

模型说明：

每只萤火虫都有自己的时钟控制发光周期，周期最开始的时候发光，然后把时钟归零，直到时钟达到最大值。 

所有萤火虫的发光周期的时长都相同，但是在setup时所有萤火虫在其发光周期中所处的时点是随机的。

萤火虫能够感知邻居发光，并据此调整自己的时钟。

萤火虫有一个参数flash-length, 是每次发光的持续时间   

另一个参数是flashes-to-reset, 这个参数是个阈值，表示当萤火虫看到这些发光的邻居时会触发它的动作。

萤火虫有两种发光策略可以选择：

延迟发光Delay：如果看到足够多的发光，那就重置发光周期，好像刚刚发完光一样。这样就可以使自己和看到的同步。

提前发光Advance：如果看到足够多的发光， 那就把时钟调整到0，使自己立刻发光。

可以通过模型试验哪种策略能导致同步。

周期蝉的“神”同步

主要内容来源于 17年蝉是怎么演化来的？--知乎 下的各回答

周期蝉是蝉科周期蝉属（Magicicada）下7种蝉的统称，其中有3种是17年蝉，4种是13年蝉。它们只生活在北美东部，其中13年蝉主要分布在美国东南部，17年蝉主要分布在美国东北部及加拿大部分地区。

这7种蝉之所以被称为“周期蝉”，是因为它们会遵循某个周期集中出现。我们以2016年为例，2016年，有一种17年蝉将会在马里兰州出现，而在2016年之后的16年里，马里兰州再也不会出现这种周期蝉，直到2033年，马里兰州才会再次出现这批周期蝉的后代。

我们一定要注意到，这种集中的、周期性的出现，和其它的蝉有着极为明显的不同。其它的蝉，都是每年都会出现的，虽然也有一些蝉有自己的成熟周期，比如3年，但是我们2016年可以见到出生于2013年的蝉，2017年可以见到出生于2014年的蝉，2018年还可以见到出生于2015年的蝉，也就是说，每年都有。而周期蝉则绝不会出现这种情况，2016年出现过的17年蝉的地区，直到2033年才会再次出现周期蝉。这才是“周期”的真正意义。

密密麻麻的趴在栅栏上的周期蝉

周期蝉的这种周期性集中出现的现象，非常独特，也十分引人注目，在周期蝉出土的年份里，你一铁锹挖下去，都能挖出几百只蝉蛹（知了猴），而每棵树上，都有几百只周期蝉再不断地向上攀爬，其密度，可以达到每英亩（大约换算成中国的6亩多一点）150万只之巨！这一壮观景象可把第一批来到北美的欧洲殖民者吓坏了，也引起了他们之中许多科学家的高度兴趣——比如著名的富兰克林——他们马上着手研究，试图搞清楚为什么这种蝉和其它蝉如此不同。为了方便研究，他们把1893至1909这17年里出现的17年周期蝉分为了17个群，以1-17编号，1893到1905这13年里出现的13年周期蝉分为了13个群，一18-30编号（没错，周期蝉的同步性只在本群内部，不同群之间则是错开的）。但是，有一些年份里，是没有周期蝉出现的，所以有些编号是空白的，也有两群周期蝉曾经出现过后来却不知道怎么的绝户了，比如编号为11的17年蝉，在1954年之后就再也没有出现过，以及编号为21的13年蝉，在1870年之后就再也没出现过，这样现在还会定期出现的周期蝉，只剩下了15组，它们的分布情况是这样的：

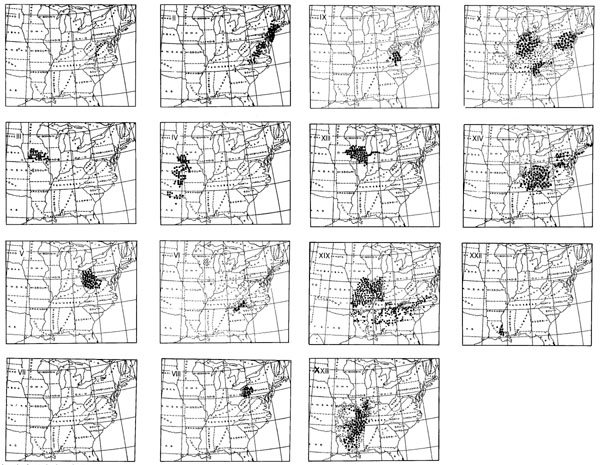
现存的15群周期蝉分布地区图，图片来自科学松鼠会@Ent

虽然科学家们绞尽脑汁的钻研，但直到今天，依然没有一个足够清晰的理论可以说明为什么周期蝉有周期，这种周期是怎么演化来的，又有何“目的”。但仍有几个假说，得到了比较广泛的支持，它们主要有：

• 周期蝉的周期，是恶劣的气候造成的
  

• 周期蝉的周期，是天敌的掠食造成的
  

第一种观念认为，周期蝉起源于180万年前，其间发生了多次冰期，在冰期，会不规律的出现寒冷的夏季，虽然蝉蛹躲在土中可以躲避严寒，但如果在冷夏出土，蝉就会冻死，而出土周期较长的蝉，可以减少族群暴露在地面上的几率，最大可能的避开了这些冷夏。有研究表明，如果假设在1500年的时间里，每隔50年左右出现一次冷夏，那么，每7年出土一次的蝉，只有7%可以躲开冷夏幸存下来，每11年出土一次的蝉，只有51%的几率可以躲开冷夏幸存下来，而17年蝉，则可以有96%的几率躲开这些冷夏！

这样看来，在那个寒冷的时代里，生命周期很短的其它蝉可能都被冻死了（今天生活在当地的短寿命的蝉，可能是从别的地方搬家过来的），只有生命周期为17年以及17年左右——比如16年或18年（注意这里，下面要讲）的蝉得以幸存。可是为什么这些蝉只有固定的周期才会出现呢？我们还可以用2016年出现在马里兰州的17年蝉为例子。它们的祖先，很可能也和其它蝉一样，每年都会出现，每次出现的都是17年之前出生的蝉，但17年蝉也有4%的几率会遇到冷夏，可能在这漫长的冰河期内，其它的周期蝉也很不幸运的遇到了4%的小概率事件，被寒冷一窝端了，只有这一组幸存至今。

我们可以看到，周期蝉的生命周期如此的长，可能是在环境的筛选之下，被逼出来的，但是环境的恶劣也是有限度的，可能北美东北部的气候恶劣程度，刚好可以让17年以及17年左右的蝉幸存下来，也可能当时也演化出了20年、30年的蝉，但昆虫的寿命也是有极限的，很难保证这些蝉都能活这么大的岁数，一边是气候的恶劣，一边是寿命的衰减，很可能刚好到了17这个年份的时候，生存率也保证了，蝉也没有老死病死的太多，两者达到了一个微妙的平衡。相应的我们可以看到，13年蝉居住的区域更为靠南，冷夏的威力更小一些，所以13年就已经有了很高的生存几率，平衡也达到了。

但是！这里有一个关键的问题：既然17年蝉可以幸存，为什么16年蝉，18年蝉没有存活下来呢？它们躲开严寒的几率，以及活到这个岁数的几率都应该和17年差不多‍‍‍

这就催生了第二个理论——周期蝉的周期性，还可能与天敌有关。

我们继续以马里兰州的这一群周期蝉为例，它们在2016年出土，数量多达几十亿只，这可把当地的鸟类、小型哺乳动物和爬行动物乐坏了，这满地都是美食，吃也吃不完，一直困扰这些蝉的天敌的食物短缺问题就这么彻底解决了，这就导致了蝉的天敌数量暴增。

我们知道，野生动物的繁殖，受到食物的影响很大，在食物充足的情况下，很多动物都会大量繁殖，幼崽也有一个很高的存活率。在周期蝉出来的那一年，许多蝉的天敌也从中渔利，生了很多后代，这些后代也顺利长大。但周期蝉的出土周期这么长，这些“超生”出来的天敌，很可能等不到周期蝉下次出土，就饿死或老死掉了，这样周期蝉下次出土的时候，天敌的种群数量又恢复到了正常水平。

但有一些天敌的数量回落，却需要一定的周期。一些动物有自己的繁衍周期，可能有的天敌要6年才能性成熟繁殖（只是举个例子），它的后代又要6年之后才会性成熟繁殖，虽然因为没有周期蝉吃，它们的种群数量一直是在回落的，但由于加入了繁殖这个因子，它们的种群衰落速度可能还没有那么快，这样到了繁殖到第三代的时候，其种群数量可能还是比当年的第一代要多……而很不凑巧的是，18年的周期蝉又出现了！天敌们又是大吃特吃，第三代天敌生下了海量的第四代天敌，其总数量，也会比18年前第一代生第二代的时候大！也就是说，这种天敌的种群数量虽然会以18年为周期下滑，但每过18年，都会迈上一个新的高度，长远来看，这种天敌的总数还是在上涨的，涨到一定的程度，就有可能把周期蝉吃的越来越少。16年蝉也是同样的道理，它很可能被一种8年繁殖一代、4年繁殖一代、甚至2年繁殖一代的天敌吃绝种。

而13年蝉和17年蝉，又幸运的避开了这个可能性。因为13和17，恰好是两个质数，什么是质数呢？也就是只能被1和它自己本身整除，也就是说，除非你每年都繁殖，或者正好17年繁殖一代，否则我几乎不会成为你繁殖的助力器，如果你2年繁殖一代，那我只会在34年之后才会遇到你的繁殖期，34年，你能活那么久吗？34年，你的种群还没有下滑到正常的水平吗？

‍这也是为什么会有很多极客把周期蝉戏称为——懂数学的蝉——的原因了。‍

不过，这个假设也有一些细节无法完美解释，比如，1年繁殖一代的动物总能遇到你吧？有的鸟类虽然6年才性成熟，但6年之后也是每年都繁殖，可以视为1年繁殖一代，你不是也躲不开吗？这些问题，可能要考虑到17年确实是一个很长的年份，许多繁殖期很短的动物，自身寿命也非常的短，还没等到下一次周期蝉出现，种群规模已经回落到很低的水平了。还有的天敌虽然6年性成熟之后可以每年都繁殖，但性成熟之后，也繁殖不了几年就死翘翘了，而它们的后代，在第17年的时候恰好只有一部分性成熟了，所以大部队又被周期蝉躲开了，种群规模还是不断地下滑。

2012年，康奈尔大学的行为生态学家沃尔特•科尼格（Walt Koenig），以及美国农业部林业局的生态学家安德鲁•利布霍尔德（Andrew Liebhold）共同发表了一个论文，他们发现在17年蝉大批出现12年后，捕食它们鸟类的数量开始减少，最终在第17年达到最低点——正是17年蝉再次大批出现的年份。以13年蝉为食的鸟类遵循着类似规律。这种情况，很可能就是我们刚才说的那样——超生的天敌因为食物匮乏开始逐渐回落——但这两位科学家也有一个新的想法：周期蝉数量如此之大，它们是否会对当地的生态环境产生了某种影响，这种影响直接影响了天敌的数量呢？但是具体是什么影响，他们现在也没法解释。

最后附送一个周期蝉的观蝉指南，生活在美东的朋友们可以按图索骥，近距离感受一下周期蝉的气势（资料来自维基百科）：

• 17年蝉第一组，将于2029年出现在Western VA, WV
  

• 17年蝉第二组，将于2030年出现在CT, MD, NC, NJ, NY, PA, DE, VA, DC
  

• 17年蝉第三组，将于2031年出现在IA
  

• 17年蝉第四组，将于2032年出现在Eastern NE, southeastern IA, eastern KS, western MO, OK, north TX
  

• 17年蝉第五组，将于2016年出现在Eastern OH, Western MD, Southwestern PA, Northwestern VA, WV
  

• 17年蝉第六组，将于2017年出现在Northern GA, western NC, northwestern SC
  

• 17年蝉第七组，将于2018年出现在Ontario, Yates, and Seneca Counties NY
  

• 17年蝉第八组，将于2019年出现在Eastern OH, western PA, northern WV
  

• 17年蝉第九组，将于2020年出现在Western VA, southern WV, western NC
  

• 17年蝉第十组，将于2021年出现在NY, NJ, PA, DE, MD, DC, VA, WV, NC, GA, TN, KY, OH, IN, IL, MI
  

• 17年蝉第十一组，已于1954年之后绝灭
  

• 17年蝉第十二组，从未发现过该组的周期蝉
  

• 17年蝉第十三组，将于2024年出现在Northern IL and in parts of IA, WI, and IN
  

• 17年蝉第十四组，将于2025年出现在Southern OH, KY, TN, MA, MD, NC, PA, northern GA, western VA and WV, and parts of NY and NJ
  

• 17年蝉第十五组，从未发现过该组的周期蝉
  

• 17年蝉第十六组，从未发现过该组的周期蝉
  

• 17年蝉第十七组，从未发现过该组的周期蝉
  




• 13年蝉第十八组，从未发现过该组的周期蝉
  

• 13年蝉第十九组，将于2024年出现在AL, AR, GA, IN, IL, KY, LA, MD, MO, MS, NC, OK, SC, TN, and VA
  

• 13年蝉第二十组，从未发现过该组的周期蝉
  

• 13年蝉第二十一组，已于1870年之后绝灭
  

• 13年蝉第二十二组，将于2027年出现在LA, MS
  

• 13年蝉第二十三组，将于2028年出现在AR, IL, IN, KY, LA, MO, MS, TN
  

• 13年蝉第二十四组，从未发现过该组的周期蝉
  

• 13年蝉第二十五组，从未发现过该组的周期蝉
  

• 13年蝉第二十六组，从未发现过该组的周期蝉
  

• 13年蝉第二十七组，从未发现过该组的周期蝉
  

• 13年蝉第二十八组，从未发现过该组的周期蝉
  

• 13年蝉第二十九组，从未发现过该组的周期蝉
  

• 13年蝉第三十组，从未发现过该组的周期蝉

‍这些关于周期蝉为什么和如何实现同步的解释到现在为止依然是假说，但我们可以非常确定的一点是：蝉是不懂数学的，更不懂什么是质数。那么北美的周期蝉种群是如何获得的这么高智商的同步繁殖策略呢？

还记得前面讲过的遗传算法吗？‍