John von Neumann                  Stanislaw Ulam

        1903-1957                             1909-1984

元胞自动机是在20世纪40年代由斯塔尼斯拉夫·乌拉姆和冯·诺依曼发明，用以证明机器的自我复制是可能的 (并进一步的将生物学与计算科学联系起来）。

初等元胞自动机(Elementary Cellular Automata，简称ECA)是状态集S只有两个元素，即状态个数k=2，邻居半径r=1的一维元胞自动机。它几乎是最简单的元胞自动机模型。由于在S中具体采用什么符号并不重要，它可取 {0，1}，{-1，1}，{静止，运动}，{黑，白}，{生，死}等等，这里重要的是S所含的符号个数，通常我们将其记为 {0，1}。

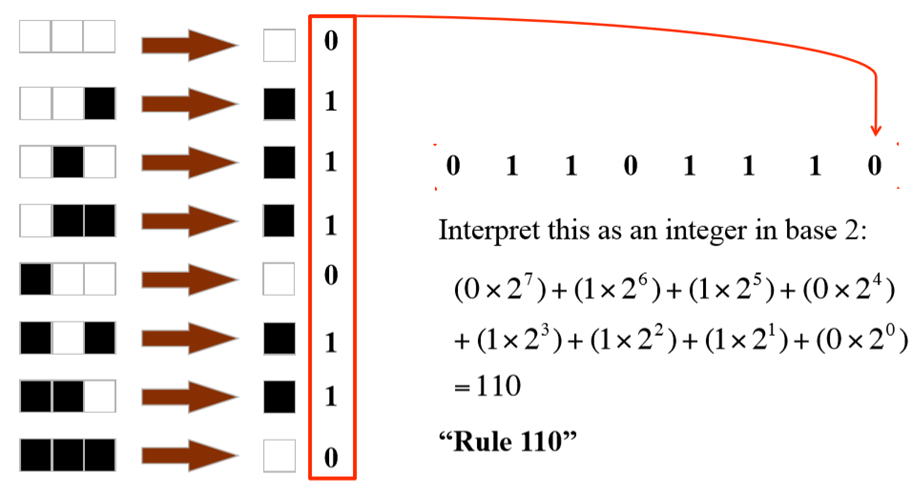
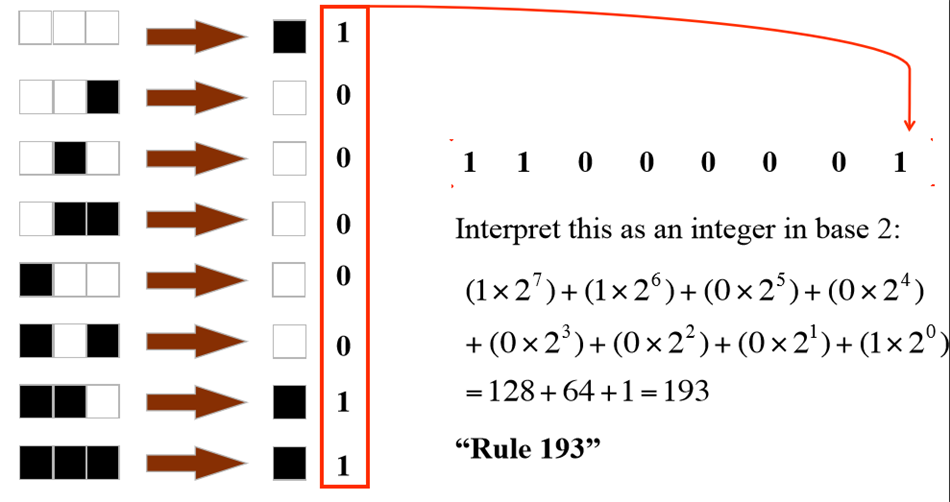
每个元胞在下一时刻的状态，由现在它自己的状态和它左右两个邻居的状态共同决定，那么就有2×2×2=8种组合。下图为其中的一个规则：

通常这种规则也可表示为以下表（映射）方式表示（黑色方块代表1，白色方块代表0）：

    

这样，对于任何一个一维的0，1序列，应用以上规则，可以产生下一时刻的相应的序列。以下序列就是应用以上规则产生的:

                                         t:   010111110101011100010
                                         t+1:  1010001010101010001

    以上八种组合分别对应0或1，因而这样的组合共有=256种，即初等元胞自动机只可能有256种不同规则。由上述八种构形产生的八个结果组成一个二进制(注意高低位顺序)，如上可得01001100，然后转换为十进制得到76，这就是这个规则的代号，则上面的元胞自动机模型就是76号初等元胞自动机 。

ElementaryCAs.nlogo(下载附件 16.83 KB)