生命游戏 (Came of Life)是J. H. Conway在20世纪60年代末设计的一种单人玩的计算机游戏。他与围棋在某些特征上略有相似:围棋中有黑白两种棋子,生命游戏中的元胞有{"生","死"}两个状态 {0,1};围棋的棋盘是规则划分的网格,黑白两子在空间的分布决定双方的死活,而生命游戏也是规则划分的网格。根据元胞的局部空间构形来决定生死,只不过规则更为简单。
J. H. Conway
下面介绍生命游戏的构成及规则:
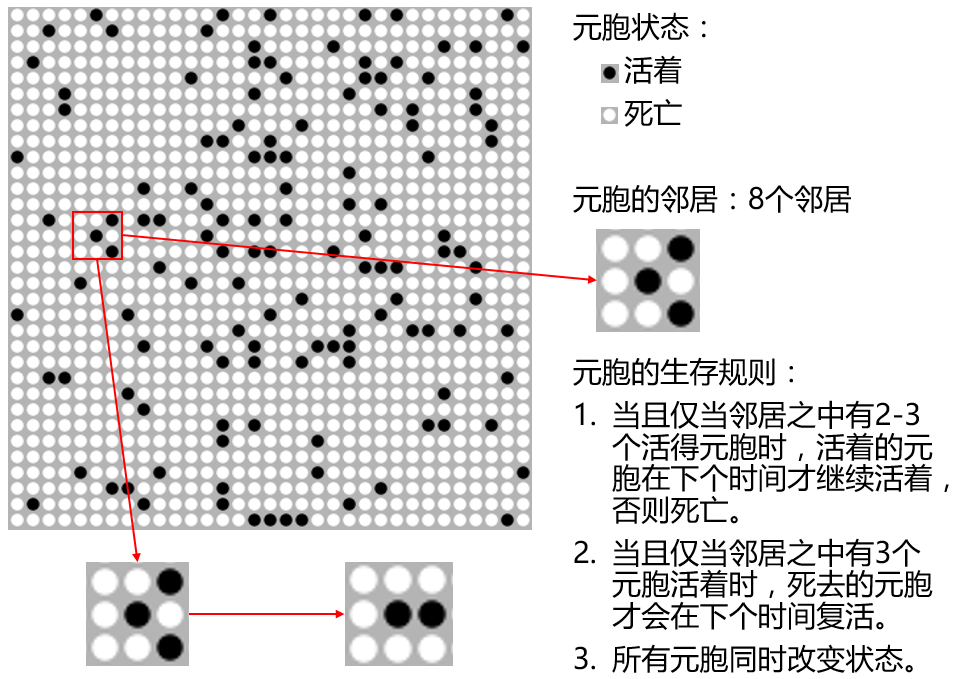
(1)元胞分布在规则划分的网格上;
(2)元胞具有0,1两种状态,0代表"死",1代表"生";
(3)元胞以相邻的8个元胞为邻居。即Moore邻居形式;
(4)一个元胞的生死由其在该时刻本身的生死状态和周围八个邻居的状态 (确切讲是状态的和)决定。
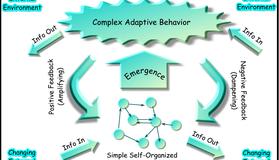
大量的简单个体通过简单规则组成的系统展现出涌现(emergence)和自组织(self-organization)
尽管它的规则看上去很简单,但生命游戏是具有产生动态图案和动态结构能力的元胞自动机模型。它能产生丰富的、有趣的图案。生命游戏的优化与初始元胞状态值的分布有关,给定任意的初始状态分布。经过若干步的运算,有的图案会很快消失。而有的图案则固定不动,有的周而复始重复两个或几个图案,有的婉蜒而行。有的则保持图案定向移动,形似阅兵阵……,其中最为著名的是"滑翔机 (叫Glider)"的图案。
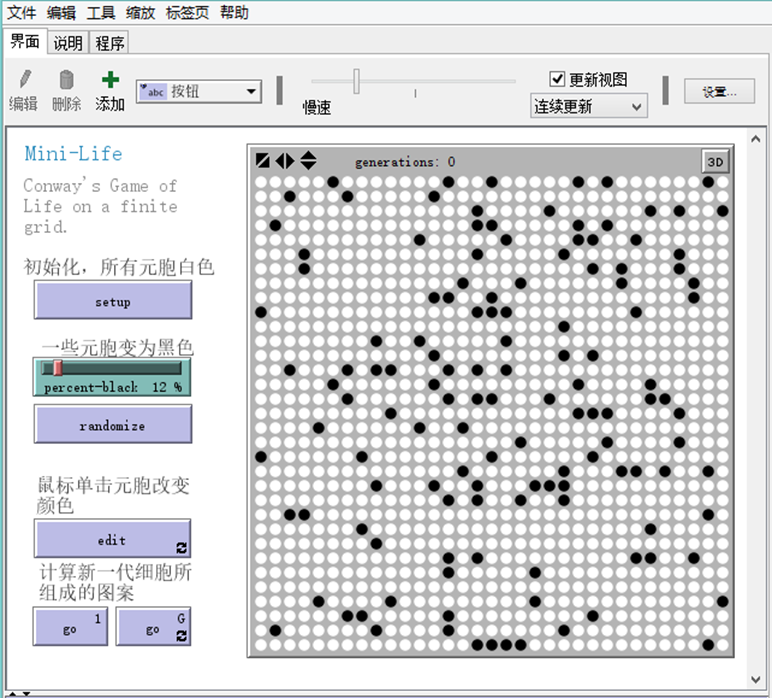
GameOfLife.nlogo(下载附件 25.56 KB)
生命游戏模型已在多方面得到应用。他的演化规则近似地描述了生物群体的生存繁殖规律:在生命密度过小(相邻元胞数之2)时,由于孤单、缺乏配种繁殖机会、缺乏互助也会出现生命危机,元胞状态值由1变为0;在生命密度过大 (相邻元胞数>3)时,由于环境恶化、资源短缺以及相互竞争而出现生存危机,元胞状态值由1变为0;只有处于个体适中(相邻元胞数为2或3)位置的生物才能生存(保持元胞的状态值为1)和繁衍后代(元胞状态值由0变为1)。正由于它能够模拟生命活动中的生存、灭绝、竞争等等复杂现象,因而得名"生命游戏"。J·H·Conway还证明,这个元胞自动机具有通用图灵机的计算能力,与图灵机等价,也就是说给定适当的初始条件,生命游戏模型能够模拟任何一种计算机。