术语：元胞自动机（外来词，纯字面翻译），也被称为”自胞自动机“。

单数：”cellular automaton” (CA)

复数：”cellular automata” (CAs)

发音：American-“cellular auTOmata”

          British- “cellular autoMAta”

元胞‍自动机的构成

元胞自动机最基本的组成元胞、元胞空间、邻居及规则四部分。简单讲，元胞自动机可以视为由一个元胞空间和定义于该空间的变换函数所组成。

1.元胞

元胞又可称为单元。或基元，是元胞自动机的最基本的组成部分。元胞分布在离散的一维、二维或多维欧几里德空间的晶格点上。

2.状态

状态可以是{0,1}的二进制形式。或是整数形式的离散集，严格意义上。元胞自动机的元胞只能有一个状态变量。但在实际应用中，往往将其进行了扩展。例如每个元胞可以拥有多个状态变量。

3.元胞空间(Lattice)

元胞所分布的空间网点集合就是这里的元胞空间。

（1）元胞空间的几何划分：

理论上，它可以是任意维数的欧几里德空间规则划分。目前研究多集中在一维和二维元胞自动机上。对于一维元胞自动机，元胞空间的划分只有一种。而高维的元胞自动机，元胞空间的划分则可能有多种形式。对于最为常见的二维元胞自动机，二维元胞空间通常可按三角、四方或六边形三种网格排列。

这三种规则的元胞空间划分在构模时各有优缺点：

三角网格的优点是拥有相对较少的邻居数目，这在某些时候很有用；其缺点是在计算机的表达与显示不方便，需要转换为四方网格。

四方网格的优点是直观而简单，而且特别适合于在现有计算机环境下进行表达显示；其缺点是不能较好地模拟各向同性的现象（前后左右与斜向的格子有区别）。

六边形网格的优点是能较好地模拟各向同性的现象，因此模型能更加自然而真实；其缺点同三角网格一样，在表达显示上较为困难、复杂。

（2）边界条件：

在理论上，元胞空间通常在各维向上是无限延展的，这有利于在理论上的推理和研究。但是在实际应用过程中，我们无法在计算机上实现这一理想条件，因此，我们需要定义不同的边界条件。归纳起来，边界条件主要有三种类型：周期型、反射型和定值型。有时在应用中为更加客观、自然地模拟实际现象，还有可能采用随机型，即在边界实时产生随机值。

周期型(Pehodic Boundary)是指相对边界连接起来的元胞空间。对于一维空间，元胞空间表现为一个首尾相接的"圈"。对于二维空间，上下相接，左右相接。而形成一个拓扑圆环面 (Torus)，形似车胎或甜点圈。周期型空间与无限空间最为接近，因而在理论探讨时，常以此类空间型作为试验。

反射型(Reflective Boundary)指在边界外邻居的元胞状态是以边界为轴的镜面反射。例如在一维空间中，当r=1时的边界情形：

定值型 (Constant Boundary)指所有边界外元胞均取某一固定常量，如0，1等。

需要指出的是，这三种边界类型在实际应用中，尤其是二维或更高维数的构模时，可以相互结合。如在二维空间中，上下边界采用反射型，左右边界可采用周期型。

（3）构形(Configuration)：

构形是在某个时刻，在元胞空间上所有元胞状态的空间分布组合。通常。在数学上，它可以表示为一个多维的整数矩阵。

4.邻居 (Neighbor)和规则(Rule)

以上的元胞及元胞空间只表示了系统的静态成分，为将"动态"引入系统，必须加入演化规则。在元胞自动机中，这些规则是定义在空间局部范围内的，即一个元胞下一时刻的状态决定于本身状态和它的邻居元胞的状态。因而，在指定规则之前，必须定义一定的邻居规则，明确哪些元胞属于该元胞的邻居。在一维元胞自动机中，通常以半径来确定邻居，距离一个元胞内的所有元胞均被认为是该元胞的邻居。二维元胞自动机的邻居定义较为复杂，但通常有以下几种形式(我们以最常用的规则四方网格划分为例)。黑色元胞为中心元胞，灰色元胞为其邻居，它们的状态一起来计算中心元胞在下一时刻的状态。

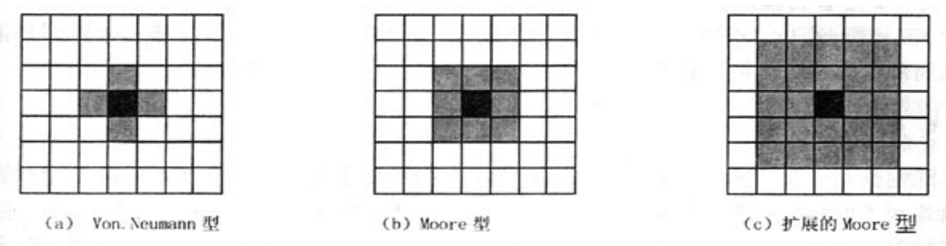
  （a）冯-诺依曼(Von. Neumann)型：一个元胞的上、下、左、有相邻四个元胞为该元胞的邻居。这里，邻居半径r为1，相当于图像处理中的四邻域、四方向。

（b）摩尔(Moore)型：一个元胞的上、下、左、右、左上、右上、右下、左下相邻八个元胞为该元胞的邻居。邻居半径r同样为1，相当于图像处理中的八邻域、八方向。

（c）扩展的摩尔(Moore)型：将以上的邻居半径r扩展为2或者更大，即得到所谓扩展的摩尔型邻居。

‍元胞自动机是复杂系统的理想化模型‍

• 由简单个体组成的大规模网络

• 个体之间有效的通信

• 没有中央控制

• 简单规则呈现出的复杂动态

• 信息处理（计算）的能力

• 能够使用GAs进化

元胞自动机的应用

• 计算机科学：

大规模并行计算架构（architecture for massively parallel computation）

分子尺度计算（molecular scale computation）

• 复杂系统：

物理、地质学、化学、生物学、经济学、社会学等的建模工具。

复杂系统的自组织和涌现等抽象概念的研究工具。

‍元胞自动机是复杂性科学中最常用的建模工具之一！

‍