‍

任务：为一个虚拟机器人进化出一套控制程序‍

                    Herbert                                                                       Robby

The Soda Can Collecting Robot                        The Virtual Soda Can Collecting Robot

(Connell, Brooks, Ning, 1988)                                                 (Mitchell, 2009)

Robby的世界是个10X10的方格棋盘，周围是墙，格子上面放着一些易拉罐。

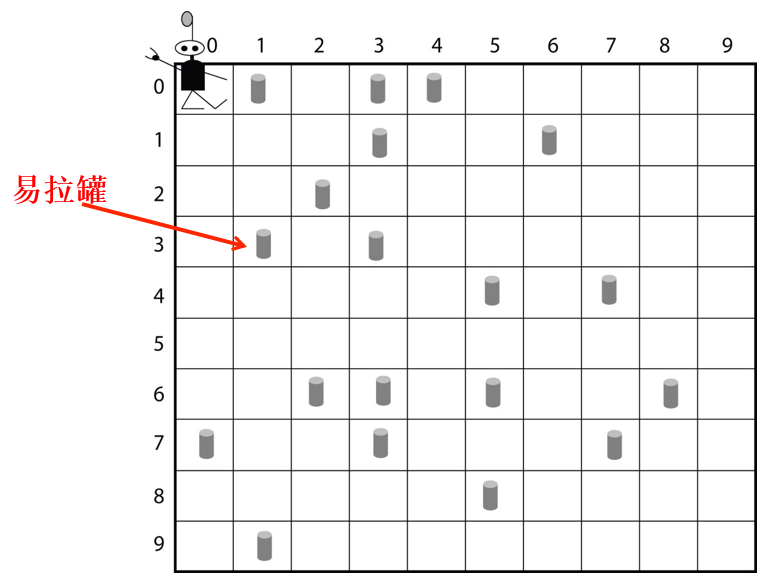
Robby能看到的东西（输入）：所在格子和上下左右四个格子（空，墙，易拉罐）

Robby能做的动作（输出）：向上移动、向下移动、向左移动、向右移动、随机移动、原地不动、捡易拉罐

Robby得到的回报（评价）：捡起易拉罐=10、撞墙=-5、捡空了=-1

‍‍目标：使用遗传算法为Robby生成控制程序（策略）‍‍

策略：一组规则，指明在所有情况下应当采取的行动。

情形：对于Robby来说，就是他看到的五个格子的内容。在Robby的世界，他会遇到的情形理论上总共有3*3*3*3*3=243种，当然有些情形实际上不存在，比如站在墙上或者左右都是墙。 

下面这个表就是一个策略：

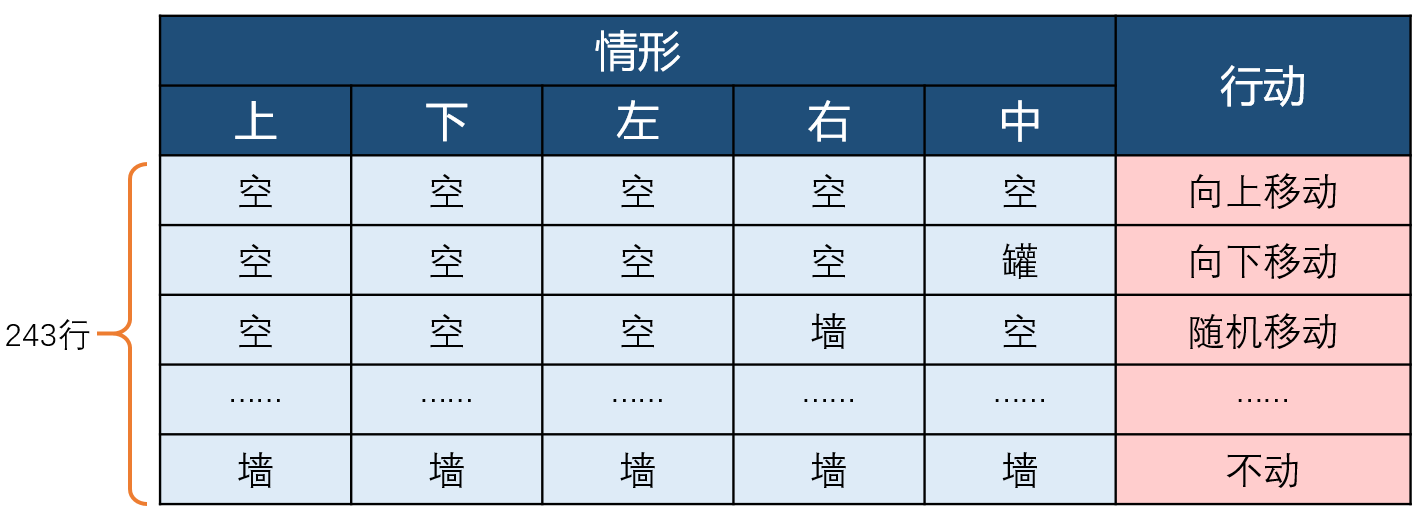
用表来表述策略太麻烦，计算机也不容易识别，因此我们对策略进行编码（Encoding）：

首先对行动进行编码：

然后对情形进行编码：将243种情形的顺序确定，然后以其行号为代码。

最后将策略表的左右两侧用代码替代，并将其转置为一串字符，情形代码为字符串的索引，动作代码为字符串上各个位的字符：

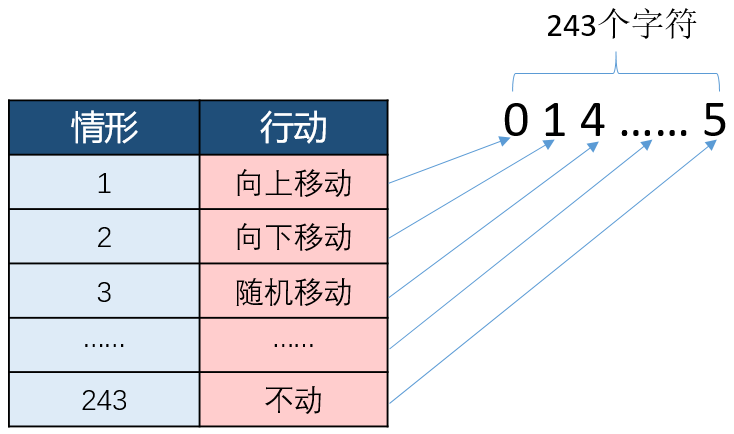
我们可以说Robby的策略有243个基因。那么Robby总共有多少种策略呢？7*7*7*....*7
GA的目标就是在这浩如烟海的可能性中搜寻好的策略。

搜寻好策略的过程是嵌套的迭代：

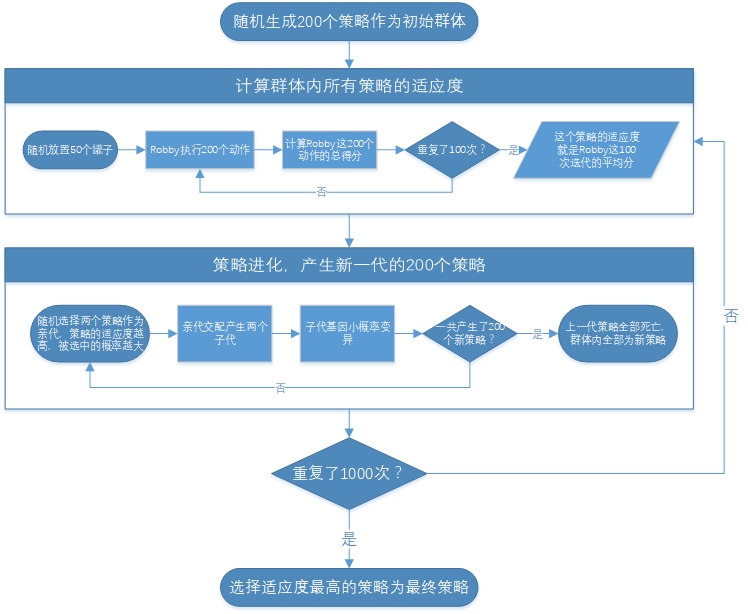
1.生成初始群体，群体内有200个随机个体，也就是200个策略。重复以下步骤1000次。

2.计算群体中每个个体的适应度（回报，得分）。

1.让Robby执行100次不同的清扫任务（约50个罐子随机放置）。

2.规定Robby在每次任务中只进行200个动作。

3.每次任务的得分就是这200个动作得分的和。

4.该策略的适应度就是这100次任务得分的平均值。

3.进化，产生新一代个体，共200个。

1.根据适应度随机选择出一对个体作为亲代，策略的适应度越高，被选中的概率越大。

2.亲代交配产生两个子代个体。（亲代基因截断互换，成为子代基因）

3.子代基因以很小的概率产生随机变异。

4.进行迭代。

每一个群体里的个体策略，看起来是这样的：

而亲代通过交配繁殖下一代的原理是基因交换：

我们在Netlogo中实现这个过程：RobbyGA.nlogo(下载附件 36.49 KB)

‍遗传算法 VS 人的智慧‍

根据上面的设定，策略的最大可能适应度大约为500。

我们想出一个自认为很“智慧”的策略：

• 如果当前位置有罐子就捡起来

• 否则，向旁边有罐子的格子移动

• 如果旁边有几个罐子，则事先设定好向哪个移动

• 如果都没有罐子，则随机移动。

用10000个清扫任务测试这个策略，结果平均得分约346。对于GA，取刚才运行的最后一代之中适应度最高的策略，用10000个任务测试，得分约486。

结果：GA 完爆人的智慧，并且几乎接近最优策略......这就很尴尬了。