维度（维数，维 dimension）Extension in a given direction。

我们通常所说的维度是拓扑维度，又称Lebesgue维度。

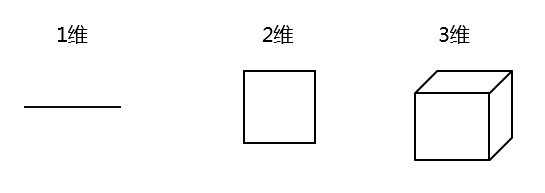
我们试着从另外一个角度计算一下维度。

将对象二等分，得到数个与原对象相似的对象：

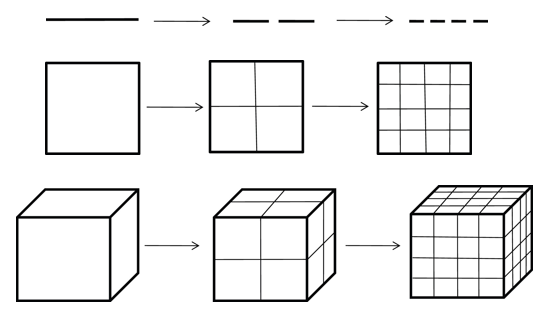
将对象三等分，得到数个与原对象相似的对象：

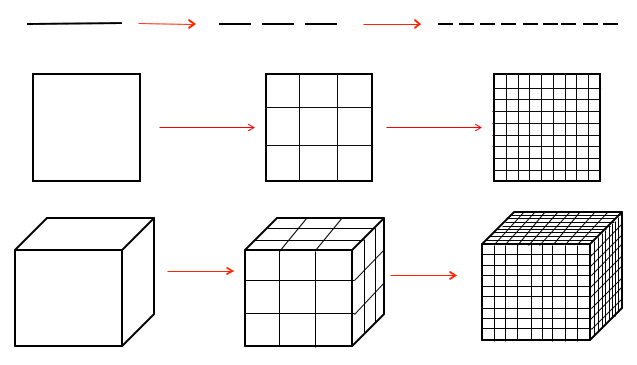
将其扩展到M等分：

1维：每一级都是由M个尺寸是1/M的上一级的复制品组成。

2维：每一级都是由个尺寸是1/的上一级的复制品组成。

3维：每一级都是由个尺寸是1/的上一级的复制品组成。

…

d维：每一级都是由个尺寸是1/的上一级的复制品组成。

令每一级的对象（复制品）数量为N，N = ，两边取对数log N = d log M，可得：

‍d = log N / log M‍

1维：N = 2, M = 2, d = log 2 / log 2 = 1  （二等分）

         N = 3, M = 3, d = log 3 / log 3 = 1  （三等分）

         ……

2维：N = 4, M = 2, d = log 4 / log 2 = 2   （二等分）

         N = 9, M = 3, d = log 9 / log 3 = 2   （三等分）

         ……

用这种方式定义的维度称为Hausdorff维度。

Lesbesgue维度定义在拓扑空间上，而Hausdorff维度定义在测度空间上。

Hausdorff维度又称为分数维度。因为它可以不是整数......

‍科赫曲线的分数维度是多少？‍

N = 4,  M = 3，所以科赫曲线的维度= log 4 / log 3 ≈ 1.26 

‍康托尔集(Cantor set)‍

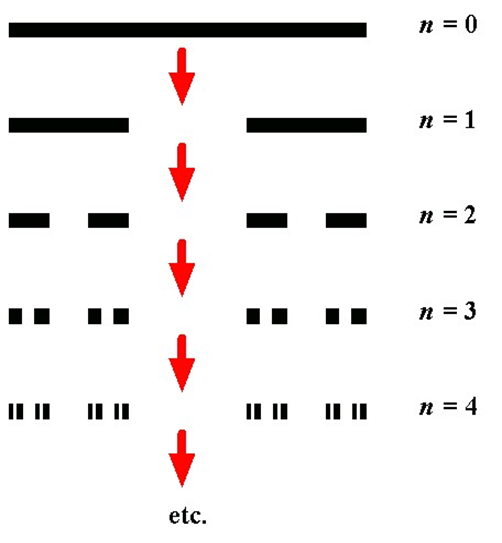取一条长度为L的直线段，将它三等分，去掉中间一段，留剩下两段，再将剩下的两段再分别三等分，各去掉中间一段，剩下更短的四段，……，将这样的操作一直继续下去，直至无穷，由于在不断分割舍弃过程中，所形成的线段数目越来越多，长度越来越小，在极限的情况下，得到一个离散的点集，称为康托尔点集，记为P。

康托尔点集的极限图形长度趋于0，线段数目趋于无穷，实际上相当于一个点集。

每次操作中，都会生成2倍数量的相似线段，而这些相似线段的程度都是上一次线段长度的1/3（三等分）。按照定义，M=3，N=2，d=log2/log3≈0.631。

所以康托尔点集分数维是0.631。

对于我们平时接触的欧几里德空间，两个定义得出的维度都是我们熟悉的维度。        
在分形集合上，他们经常不同。比如康托集合，Lesbesgue维度是0，Hausdorff维度是ln2/ln3。  

上面的图形叫谢尔宾斯基地毯，他的维度是多少？

这些图形都叫分形图形。分形图形的基本特征是具有标度不变性。即在使用不同的尺度下观测分形图形时所得到的结果是具有相似性的，分形图形具有尺度上的对称性。这种特性表明，不同的尺度（大小）的同一种分形图形之间具有某个共同的几何参数，即这一参数是一个与尺度大小无关的不变量，这个量就是分形集合中的分数维度。

分数维度到底有什么用呢？回想我们在3.1节中提到的英国海岸线无限长的问题。为什么说英国海岸线可以无限长？就是当我们选择用不同刻度的尺子去量海岸线的时候，海岸线的长度也就不一样，因此，当我们选择用更加精确的尺子去衡量海岸线的时候，长度就因此会变的更加长，所以这才会有分形理论的最经典的例子。而分形维数在这个例子当中的体现，就是你选择的尺子的型号。分形维数另外一方面也是一个标准，就是说明这个几何图形的变化情况，同时也阐述图形的复杂和粗糙程度。

但是，Hausdorff维度有着严格的数学定义，并且很难计算......

下次吃饭看到盘子里的菜花时，会不会有些异样的感觉？