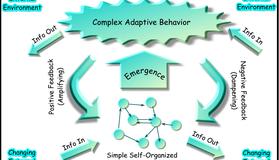
自然界之中到处都是看起来很相似的形状：树枝、菜花、叶脉、水波、山峦，一些人造物也表现出同样的特点，例如互联网。

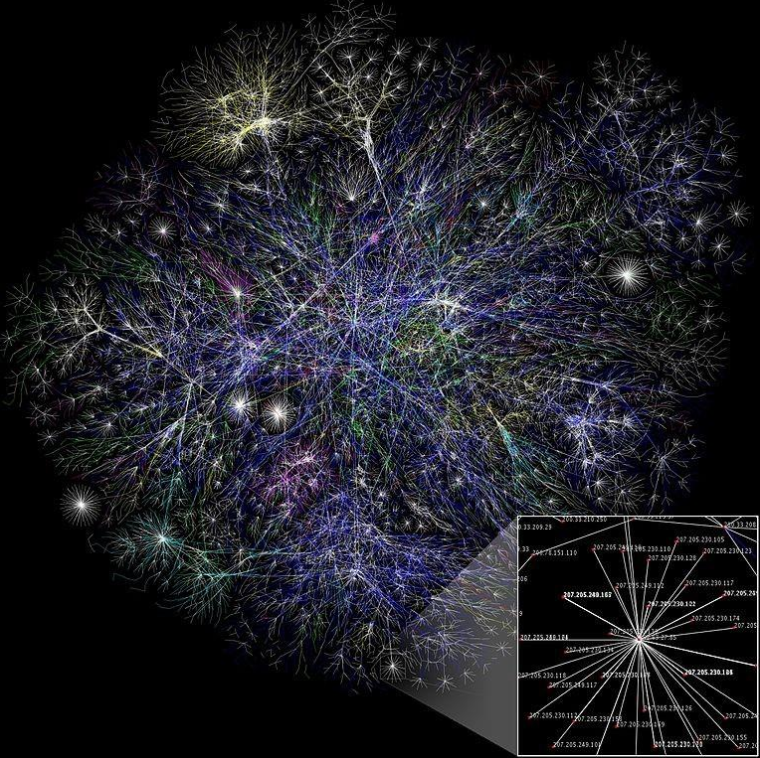
这些都是“分形”。数学中的分形精确而严谨，自然界中的只是近似分形，或者说是自相似（self-similarity）。

分形之父：Benoit B. Mandelbrot

本华•曼德博

Benoit B. Mandelbrot

1924.11.20 ~ 2010.10.14

曼德博的研究范围广泛，从数学物理到金融数学，但他最大的成就则是创立了分形几何。

他创立了“粗糙理论”和“自相似性”并用分形几何完成了证明。他创造了“分形”一词，随后又发现了曼德博集合，用于描述那些复杂的、无穷尽的分形形状。为了纪念他在分形上的巨大贡献，该集合以他的名字命名 。

他也致力于向大众介绍自己的理论，通过面向普通公众的著作和演讲，使他的研究成果广为人知。

曼德博在耶鲁大学的个人主页

注：Mandelbrot的名字有好多种中文译名，但是“本华•曼德博”是他本人确定的中文名。

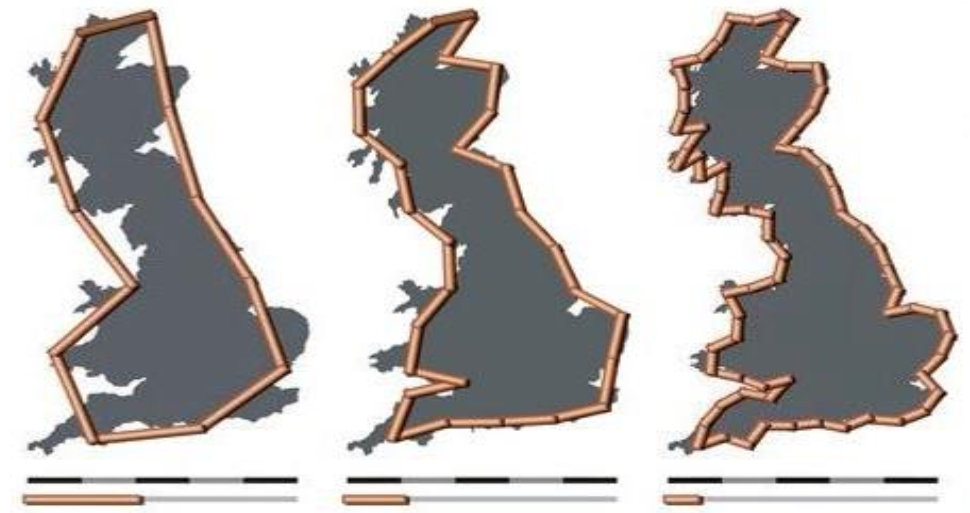
博德曼关于分形的著名例子：英国海岸线到底有多长？