SimplePopulationGrowth.nlogo模型中的初始人口增加到2，那么每一步的总人口会是初始人口为1的时候的2倍。不论模型运行多少次也不会改变。

将初始人口增加到5呢？增加到20呢？......

‍这就是线性系统，即整体等于部分之和。因为系统内的成员没有相互作用，系统也没有与环境相互作用。‍

我们加入一些影响因素，例如因为环境拥挤造成的死亡。

‍这就是逻辑斯蒂模型(Logistic Model)‍

任何一个物种都有使其种群无限增长的内在潜力（即所谓指数增长），这是生命设计的基本原理，失去这种特性的物种其命运就是灭绝。而环境的有限性将阻止这种趋势的无限发展，使其趋于一个平衡值K（即所谓的环境容量），种群大小N越接近K，环境阻力越大。 

再来看看指数模型和逻辑斯蒂模型种群的增长速率的变化。在指数增长模型中，随着时间t的增大，种群数量P的增长速率（即单位时间增加引起的种群增加量）也越快，t趋于无穷大时，P的增长速率也趋于无穷大。而在逻辑斯蒂模型中，开始随着t的增加，P的增长速率增加，当P为K/2时，P的增长速率达到最大，之后，t的进一步增加，P的增长速率不断减慢，最后趋于0。

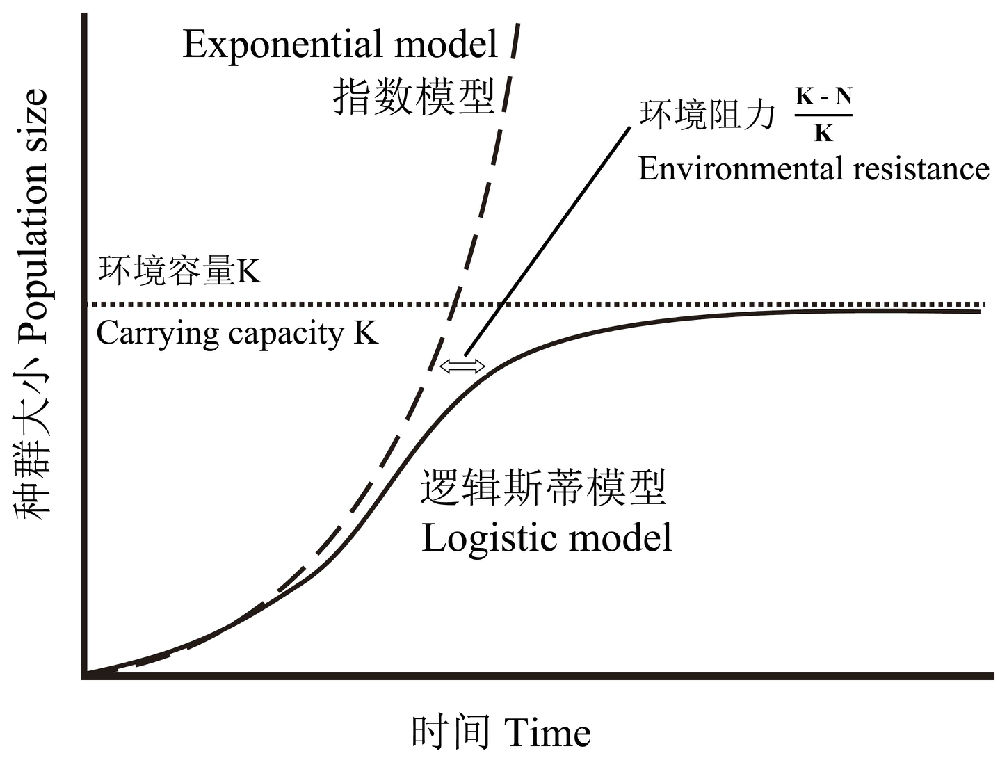
值得注意的是，在P达到K/2之前，P的增长近似于指数增长，即在近乎理想的条件下，逻辑斯蒂模型的初始阶段为指数增长，而K/2是种群增长速率的拐点。因此，逻辑斯蒂模型的本质是一种描述种群数量从初始的指数性（无限）增长向环境容量逼近的动力学过程。

在NetLogo中，可以通过修改上一节的指数增长模型得到逻辑斯蒂增长模型。

根据逻辑斯谛模型我们加入deathrate参数，新繁殖的一窝兔子，会有deathrate只夭折。

所以如果要和简单增长模型一致，应设定brithrate=3，deathrate=1 。

‍在LogisticModel的模型中增加初始人口，看看刚才的简单增长模型是否一样？

LogisticModel (new).nlogo(下载附件 13.67 KB)

‍结论：非线性系统是不可加的。‍