阅读方差分析的由来，思考：单因素完全随机方差分析、单因素随机区组完全随机化方差分析、两因素完全随机方差分析、两因素重复测量方差分析、混合设计的F值的分子和分母分别是什么？

来源：微信公众号马同学图解数学

1 费希尔的简介

罗纳德·艾尔默·费希尔爵士（英语：Sir Ronald Aylmer Fisher，1890－1962，），英国统计学家、演化生物学家与遗传学家。现代统计学与现代进化论的奠基者之一。安德斯·哈尔德称他是“一位几乎独自建立现代统计科学的天才”：

方差分析、F分布，都是费希尔的贡献，这些统计方法可以说完全改变了人类进行科学研究的方式方法。

2 耙粪堆

费希尔有着惊人的数学才能，他在1912年获得剑桥大学的数学学位的同时，还斩获了当年剑桥大学的“牧人”头衔，这需要通过一系列难度极高的口头和书面的数学考试，每年都只有一两位学生可以成为“牧人”，有的年份甚至无人可以荣膺。和黎曼类似，在他的一些重要论文，他认为其中很多数学结论非常显而易见，不屑于证明。后来由瑞典数学家哈拉尔德·克拉梅尔等数学家进行了梳理、补充和证明，才逐渐扩充成为了现代统计科学的重要组成部分。

1919年，罗森斯得农业实验站的主任约翰·拉塞尔爵士发出了邀请，希望费希尔来查看下该实验站历年收集的数据中到底藏有什么秘密（下图是罗森斯得农业实验站）：

由于种种原因，费希尔的生活并不顺利，看在一年1000英镑的份上，费希尔带着他的家人，来到了这个伦敦以北的农业地区，蹬上靴子，穿过农田，取出巨大库房中、堆积如山的、积累了90年的数据，开始了他所谓的“耙粪堆”的工作。

3 方差分析

罗森斯得农业实验站很重要的一个工作就是，搞清楚施用不同的混合肥料，马铃薯的产量是否会不同。费希尔的做法是在农田中种上马铃薯，不同部分施用不同的混合肥料（下面是一个示意图，在同一块农田的不同排施用不同的肥料，然后插上牌子进行区分）：

然后在收获后对数据进行采样，看不同实验组的产量是否不同。

3.1 两个问题

费希尔也知道，马铃薯不是什么工业产品，本身产量就会有波动，肯定不能说某个实验组产量多了 20% 就说该组施用的混合肥料有效果，至少需要考虑以下两个问题：

        （1）概率。马铃薯的产量 X 本身具有随机性，比如说服从某正态分布：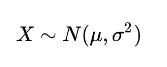

根据该分布，产量在-20%-20%之间波动可能性较大，因此如果某实验组产量多了20%，并没有把握说混合肥料产生了效果（因为不可能知道所有马铃薯的产量，所以无法真正算出 μ， 也就不可能真正知道该正态分布 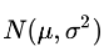，因此用虚线画出）：

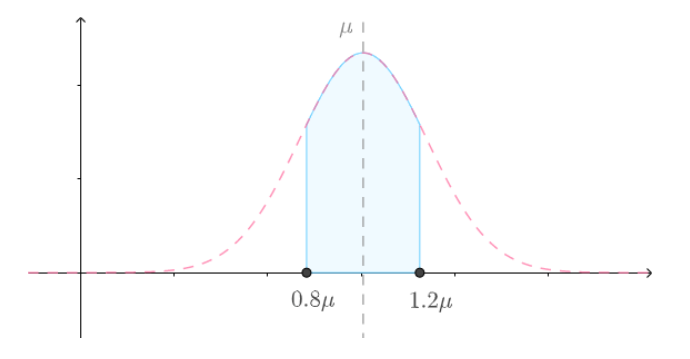
而产量在50%之上的波动可能性较小，因此如果某实验组产量多了50%，那么说明混合肥料可能真的产生了效果：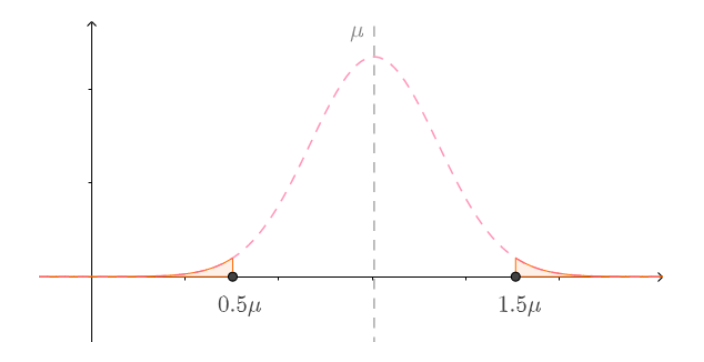

（2）原因。马铃薯的产量X如果是随机波动，那么应该是有增有减的。比如从某个实验组中采样得到五株马铃薯，记录每株的重量，得到五个点。算出该实验组的平均产量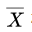相对于μ增加了20% ，并且五个点相对于μ有增有减，分散在的四周，这就说明重量变化是由于随机波动造成的：

如果某个实验组平均产量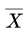相对于μ还是只增加了20%， 但组内所有的马铃薯植株上的产量都是增加，紧密的围绕在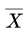的附近，那么说明混合肥料可能真的产生了效果，造成组内所有马铃薯的重量都增加了：

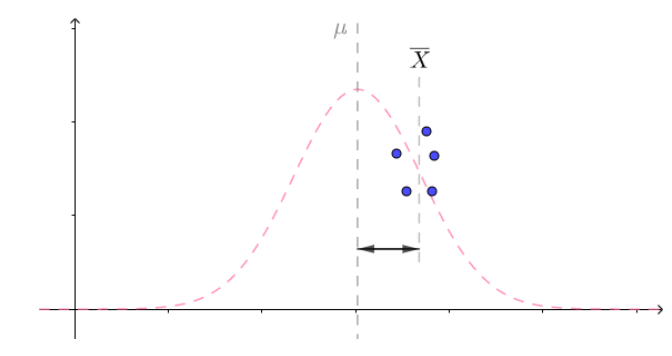
就此，费希尔设计了 组内方差 这个统计量，当组内方差较小的时，说明该试验组的普遍增产（或减产），也说明混合肥料可能真的产生了效果（组间方差、组内方差这两个统计量接下来会进一步介绍）。

3.2 假设检验

综合上面两个问题，费希尔设计了一个假设检验（关于假设检验，可以参考这里）：

• 假设：混合肥料没有效果，也就是各个实验组的产量的均值相同

检验：设计了这个统计量，当实验组得到的数据使得该统计量足够大时，那么就可以推翻上述假设，得到混合肥料有效果的结论

从抽样到计算完成该假设检验，就称为 方差分析 。

4 实战

下面用具体的数据进行下实战讲解。假设有 A、B、C 三组马铃薯，每组施用不同的肥料。在每组中各选五株，记录每株产出的马铃薯的重量，所得表格如下（下面的重量也是为了本文讲解设计的，不用较真）：

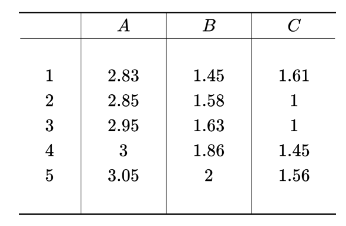
根据上面表格，画出来的图像是这样的：

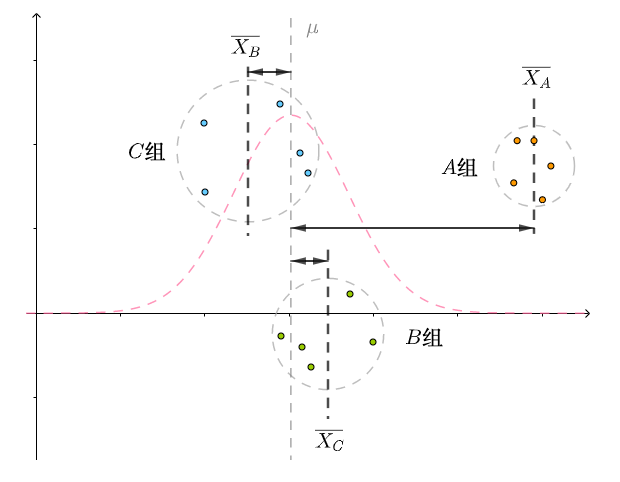
可以看出：

• 发生了低概率事件，即 A 组的样本均值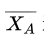远离μ

• 原因很可能是由于混合肥料导致，因为 A 组整体都增产了，而不是随机波动

所以是很有把握认为这三组产量不同，并且是由于混合肥料导致的。当然上面是定性分析，下面看看如何定量分析。

4.1 组间方差

首先需要知道发生了低概率事件，即是否有某组（在本例中是 A 组）的样本均值远离μ 。因为μ是没有办法真正知道的，实际计算时只能用所有样本的均值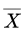来代替（本例中就是15株马铃薯的均值），然后计算各个实验组的样本均值与 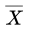的距离，累加起来就得到了组间方差：

4.2 组内方差

将各个实验组的方差加起来就得到了组内方差（其中也多了些常数，暂时可以不用管）：

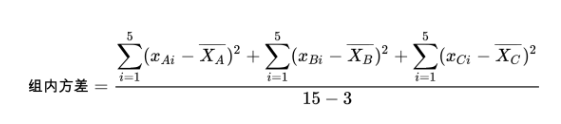
其中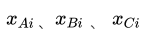就是各组内的某株马铃薯的重量。组内方差越小，说明各个实验组变换越一致，越有可能是由混合肥料导致的。

4.3 统计量构造

费希尔接着构造了这么一个统计量，它综合了“概率”和“原因”这两个角度。为了说明这点，我们又对之前的 A、B、C 三组进行了多次实验，得到不同的组间方差、组内方差：

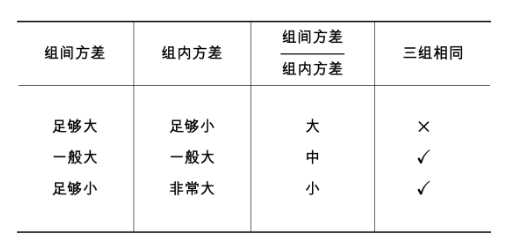
解读下：

• 第一行，组间方差大，说明可能发生了低概率事件；组内方差小，说明组内变化可能一致。本文的例子算出来就是该行。那么有充分的理由相信，这三组中其中某组（也可能是某两组、某三组）的产量有所不同，并且这种不同很可能是由于混合肥料造成的

• 第二行，组间方差一般大，组内方差也是一般大，没有充分的理由相信这三组是不同的，保守一点，我们判断这三组是相同的

• 第三行，组间方差足够小，说明可能没有发生低概率事件；组内方差足够大，说明可能组内的变化不一样。那么还是保守地判断这三组是相同的

可见统计量越大，那么三组不同的可能性越大。那具体要大到什么程度，才有把握说三组是不同的呢？这就需要F分布进行最后的检验（F就是Fisher的首字母，所以你也可以称之为费希尔分布）。

4.4 F分布

可以证明，满足某些条件的情况下（比如总体和样本都是正态分布），统计量

是服从F分布的：此时，当的值足够大，大到落入F分布的右边区域（也称为拒绝域）时，就有把握说三组是不同的：

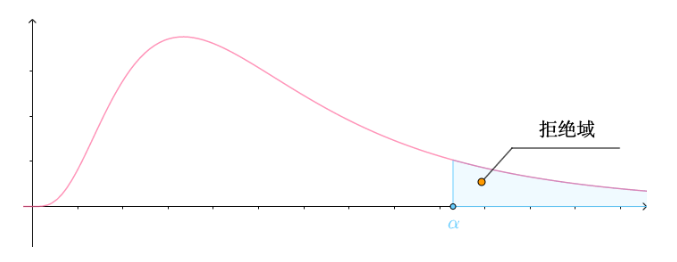
至此就完成了假设检验，也就是完成了方差分析：

• 假设：混合肥料没有效果，也就是各个实验组的样本均值相同

检验：计算统计量 的值，如果所得值落入F分布的拒绝域，那么就拒绝原假设，否则就接受。