阅读正态分布的3个重要问题,理清自己的学习误区,并反思自己还有哪些疑惑之处?
来源网址:一文搞懂“正态分布”所有重要知识点 (qq.com)
(提示:选中网址后面内容,将出现笔形图,点击后将出现文章来源网址)
1.连续型随机变量研究区间概率
了解了正态分布的基本思想,我们来看看实际应用中我们需要掌握的要点。首先,正态分布属于“连续型随机变量分布”的一类。我们知道,对于连续型随机变量,我们不关注“点概率”,只关注“区间概率”,这是什么意思?
我们看这个例子,假定随机变量X指是“北京市成年男子的身高”,理论上它可以取任意正数,所以我们把它当做一个连续型随机变量(连续型变量,就是指可以取某一区间或整个实数轴上的任意一个值的变量)来看待。这里,我们先想一想如何计算P(X =1.87)? 即身高恰好完全exactly等于1.87的概率是多少,这就是所谓的“点概率”。更极端一点,让随机变量Y是[0,1]这个区间上的任意一点,那么Y的取值有多少个呢?无数多个,我们数不清楚,所以Y 取某一个具体的值的概率是1除以无数,即可以看做是0。于是,这里透露一个很重要的结论:连续型随机变量取任意某个确定的值的概率均为0。因此,对于连续型随机变量,我们通常不研究它取某个特定值的概率,而研究它在某一段区间上的取值,比如身高在1.70~1.80的概率。
2.概率密度函数
对于初学者来讲,“概率密度”可能是最不友好的一个概念,直接谈概率不行吗,好好的为什么要生出一个“密度”?的确,没有太多数理基础,这个概念着实不太好理解。虽然文字和数学公式上你可能感觉很陌生,但我们特别熟知的那条中间高、两边低的“钟形曲线”恰恰就是正态分布的概率密度曲线。前面我们讲了区间概率,这里你就可以通过区间的角度来理解概率密度曲线:曲线越高,也就代表着这个区间的数据越密集,简单理解成在同样大小的房子里,这个房间的人数更多、更挤。除此之外,另一个关于概率密度函数的重要知识点是,积分(这里简单理解为“密度曲线下面积“即可)等于概率。随机变量X在某个区间比如(a,b)即a<X<b的概率,就是概率密度曲线在这个区间下的面积,数学上的表达就是密度函数在区间(a, b)上的积分。所以,概率的大小就是“概率密度函数曲线下的面积”的大小,这个不太起眼的概念实际上就决定了你日后是否能理解假设假设中所谓的“拒绝域”。
下图中的三条曲线f(x),就是概率密度函数,各种形式的概率就是相对应的曲线下面积。这里,数学基础不太好的同学不用特别深挖积分的计算过程,但对这三张图与对应的概率表达形式,同学们要熟知。

3.标准化与查表求概率
接下来,我们通过一个例子来看如何通过查表法计算正态分布变量在某个区间的概率。首先,我们看这个问题,说小明每天上学的通勤时间是一个随机变量X,这个变量服从正态分布。统计他过去20天的通勤时间(单位:分钟):26、33、65、28、34、55、25、44、50、36、26、37、43、62、35、38、45、32、28、34。现在我们想知道他上学花30~45分钟的概率。
首先,我们将问题转化为数学表达式,要算他上学花30~45分钟的概率,就是求P(30 < X < 45)。之前我们一直强调,一个变量服从正态分布,就要立马考虑到它的均数和标准差是多少。这里我们简化一下用他过去20天的样本数据来代替。所以,我们首先计算这20天通勤时间的样本均数及标准差,分别为38.8(分钟)和11.4(分钟)。
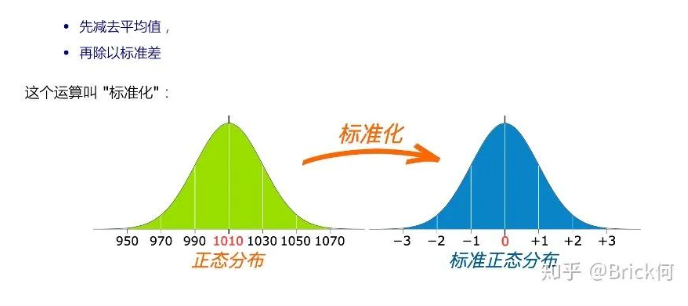
然后,我们进行标准化,这一步很重要,也称z变换。通过标准化,所有服从一般正态分布的随机变量都变成了服从均数为0,标准差为1的标准正态分布。对于服从标准正态分布的随机变量,专门用z表示。因此,求P(30 < X < 45),就转换成了求P(-0.77 < Z < 0.54),标准化的具体计算为:
30 →(30-38.8)/ 11.4 = - 0.77 45 →(45-38.8)/ 11.4 = 0.54 X → Z P(30 ≤ X ≤ 45)= P(-0.77 ≤ Z ≤ 0.54)
这里简单提醒一下,经过标准化后,原来的曲线的形状不会变化,即不会改变胖瘦,只是位置发生平移,比如下图中的例子,经过标准化实际上只是均数从1010移到了0。