假设检验的思想

来源网址：假设检验的思想|聊聊统计学史上最著名的女士品茶 - 知乎 (zhihu.com)

（提示：选中网址后面内容，将出现笔形图，点击后将出现文章来源网址）

那是20 世纪20 年代后期，在英国剑桥一个夏日的午后，一群大学研究院、他们的太太，还有一些其他客人正围坐在户外的桌旁，享用着下午茶。

我们知道，英国人有300多年的饮红茶历史，英国下午茶是英国人一项一直延续到今的传统，有人还曾经说过，没有一个国家对红茶的品鉴水准可以超得过英国。

在品茶过程中，一位女士，穆里尔.布里斯托博士，她强调，把茶加进奶里，或把奶加进茶里，不同的做法，会使茶的味道品起来不同。

开始的时候，在场的一帮科学家们，对布里斯托博士的观点表示很可笑，因为两者最后的混合物的成分是一致的，怎么可能会由于先加茶还是先加奶的顺序不同，茶就会有不同的味道呢？

然而，在座的一个身材矮小、戴着厚眼镜、下巴上蓄着的短尖髯开始变灰的先生，却不这么看，他对这个问题很感兴趣。当时他兴奋地说到，“让我们来检验这个命题吧”

这个就是我们故事的另一个主角，现代统计学奠基人之一的费希尔

不看背景的话，这听上去虽然有点像午后精英们的小消遣，但显然我们的男主角确实是很认真的，因为他把这个试验的详情认真地记录在他1935年的著作《试验设计》当中。现在《试验设计》已经成为了数理统计的一个分支，统计学专业的学术的必修课程之一。

在这个试验当中，费希尔一共煮了8杯茶，其中有4杯是先加奶的，而剩下四杯则是先加茶。这8杯茶被装在外观一样的茶杯当中，以随机的顺序被送去给布里斯托博士品尝，她需要在品尝之后分辨出哪些是先加奶的，哪些是先加茶的。

试验开始，第一杯茶杯送过去，布里斯托博士品尝了一会儿，开始确认这一杯是先加茶还是先加奶。然后第二杯被送过去，第三杯被送过去，…，第八杯被送过去。试验结束了，在场的各位科学家门惊奇地发现，她竟然真的判断出每一杯茶的正确制作方式。

在《试验设计》这本著作当中，费希尔设计了各种试验方法，去确定这位女士是否能够正确区分，这个试验的一个关键问题在于，无论是何种试验，对于没有任何分辨能力的人也有可能全部蒙对，例如如果只是一杯茶，对于没有任何区分能力的人来说，也有50%的可能蒙对。（相反，即使是有很强的区分能力，也有可能因为某些原因，失手猜错）。

那么回到本次试验当中，布里斯托博士需要在8杯茶当中正确分辨出哪4杯是先加奶的。不妨让我们先假设，假设布里斯托博士并不具备真实的分辨能力，而只能随机猜测的话，要正确分辨出的可能性有多少？

这个命题类似于我们在古典概型中的抽球游戏。游戏箱子中一共有4个白球，4个红球，我们随机从中抽出4个球，其中4个均白球的（分辨出4杯先加奶）的概率是多少？借助排列组合的思想，我们以X作为抽到白球的数量，X的取值范围是[0,1,2,3,4]。通过排列组合的公式，我们可以计算得到各个组合的分布分别是：

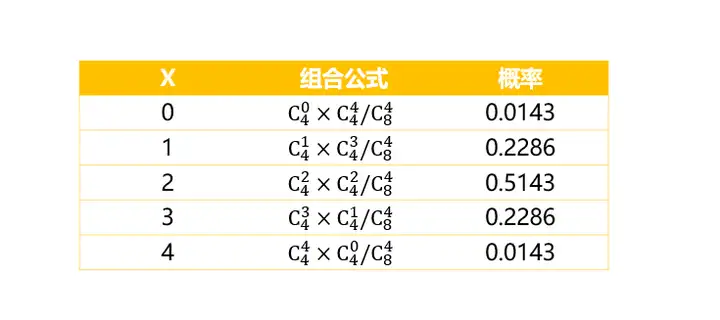
从上面的排列组合结果中，我们可以看到，如果布里斯托博士对先加奶和先加茶是没有分辨能力的话 ，要全部猜对的概率仅为1.43%，由于这个概率很小，所以我们有充足的理由认为我们原有的假设“布里斯托博士并不具备真实的分辨能力”很有可能是错误的，她确实能否正确区分。

实际上，上面就是我们做的一次假设检验，接下里，我们重新梳理一下我们的在假设检验的步骤：

首先，我们构造两个假设，第一个假设称之为原假设（H0），第二个假设我们称之为备设假设（需要注意的是，备设假设为原假设的否定命题）

H0：布里斯托博士并不具备真实的分辨能力

H1：布里斯托博士具备真实的分辨能力

之后，我们构造一个与此相关的统计量，并计算原假设成立的情况下，该统计量成立的概率是多少（此处说法多少有些不严谨，但是不影响主要理解），而这个概率就是我们经常可以听到的P值。

假如这个概率很小，小到我们认为几乎不可能发生，那我们就可以拒绝原假设，接受备设假设。其实这里面体验的就是一种“小概率反证”的思想。即原假设成立的前提下，小概率事件在一次试验中不太可能发生，如果发生了，则认为原假设并不成立。

现在，另一个问题，多小的概率我们称之为小概率，有些人觉得0.1可能算得上叫小概率，有些人则可能觉得0.01才能算得上叫小概率。一般来说，我们习惯吧这个小概率的阈值定在0.05，我们把这个检验阈值称之为检验水平。即把发生概率小于0.05的事件称之为小概率事件，当一个事件发生的概率小于0.05时，我们认为可以有充足的理由拒绝原假设。在女士品茶这个试验当中，p值仅为0.0143，要小于0.05，所以可以认为布里斯托博士具备真实的分辨能力，能够区分出来先加奶还是先加茶。