阅读后思考:如何开展相关研究更科学?
谨慎陷入相关性的误区——相关关系不等于因果关系 - 知乎 (zhihu.com)
(提示:选中网址后面内容,将出现笔形图,点击后将出现文章来源网址)
有些数据分析爱好者在研究事物间关系时,分不清函数关系、相关关系和因果关系,甚至把相关关系和因果关系混为一谈,导致最终研究结果跑偏。
实际上,这并不是只有普通研究者才会犯的错误,权威期刊《新英格兰医学期刊》曾刊登过一篇论文,论文的作者是纽约哥伦比亚大学的弗朗兹·梅瑟利博士,他发现 “一个国家人均巧克力消费量和这个国家获得诺贝尔奖的人数有着密切关系,人均巧克力消耗越多,获得诺贝尔奖的概率也越高”。
该研究结果发表后,在当时引起了极大的关注和争议。有人调侃道: ”瑞士、瑞典和丹麦的巧克力消费量位居前三,而美国的排行居中,若美国想多一位诺贝尔奖得主,每年需多摄入1.25亿公斤可可,而瑞士的人均摄入可可量每年高达3.4千克。”
2001年诺贝尔物理学奖得主埃里克・科内尔则认为该项研究可能毫无意义。

在研究中,若随意在两种事物上寻找关联,就会犯“巧克力决定诺贝尔奖得主”这类没有逻辑的关联错误。
本期内容,小编将带着大家从概念上对函数关系、相关关系和因果关系做一个简要梳理,帮助大家建立相关性的逻辑认知,最后着重给大家介绍统计学上常见的相关关系及其方法应用。
变量之间的关系有哪些?
在统计学中,根据变量之间的关系或数据类型,可将其之间的关系分为函数关系和相关关系。
函数关系
所谓函数关系,是指各变量之间的数值根据一个函数表达式形成对应关系,是一组严格确定的依存关系。当一个变量取一定值时,另一个变量有唯一的一个值与之对应。
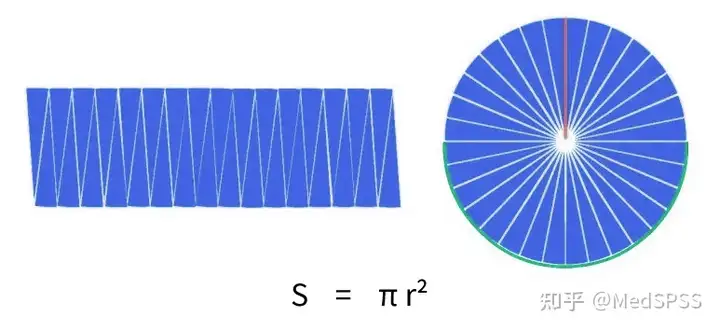
例如计算圆面积的公式:S=π*r^,当已知圆的半径r,就可计算出圆的面积S。
即圆的面积S与圆半径r为一组函数关系。
变量之间的函数关系在自然科学中是普遍存在的,一些自然科学中的定理和公式都可理解为函数关系,这些函数关系揭示了变量之间存在的确定关系或作用。
相关关系
相关关系,是指变量数值间存在着非严格的依存关系。当一个变量取某个值时,另一个变量的值是不确定的,但是该变量的值会随着前一个变量的数值发生一定的变化规律。
例如人的年龄与体脂含量的关系:对于个体来说,同样年龄的人,体脂含量不一定相同,但是对群体来说,却出现体脂含量随着年龄增加而增高这一变化规律,这就是一种相关关系。
重点来了,在相关关系中,可能会出现以下几种特殊的情形,这也是为什么人们容易“误解”或“混淆”相关性。
1、因果关系。例如,一块农田的施肥量与小麦产量的关系,这既是一种相关关系,同时也是一种因果关系,施肥量是因,小麦产量是果。
2、相互依存的关系。例如,夜间睡眠质量与快乐指数具有相关关系,但在夜间睡眠质量与快乐指数的关系中,较难确定哪一个是因,哪一个是果,两个变量是相互依存的。在没有绝对理论依据的情况下,重联系,轻结论。
3、只存在数值上的相关关系。例如,有人将冰淇淋销量与溺水人数进行分析,发现这两者之间具有正相关关系:冰淇淋销量越高,溺水人数越多,这只是一种虚假的相关关系。上文提到的巧克力消费量和这个国家获得诺贝尔奖的人数就是一种典型的虚假相关关系。



