形成性考核题目：

一、文字接龙：利用文字接龙的形式将中国20名科学家与20名外国数学家形成一个闭环，并给出各位科学家及数学家的简介。

二、测量：仅用一张A4纸与计算器测出聊城市电视塔（聊城市柳园路与财干路的东南角）的高度。

三、数独：编写一个程序，计算出3*3，4*4，5*5的个数。

四、勾股定理：勾股定理的证明现在发现已经有400多种证明方法，请您举出5种，并简要说出中西方证明方法各具有些特点？

五、花草：用数据体现至少20种花草的叶绿素含量，并说出这些花草如何更好的养殖。

六、线路：某装修公司要在某建筑物内铺设线路，在线路中需要7米、5米、4米三种不同规格的PTC管，分别至少180根、210根、160根，现购置了一批规格为16米的PTC管若干，如何截取才能使用料最省？

七、物流：某公司在三个地方有三个分厂，生产同一种产品，其产量分别为300箱、400箱、500箱。需要供应四个地方的销售，这四个地方的产品需求分别为400箱、250箱、550箱、200箱。三个分厂到四个销地的单位运价如表所示。

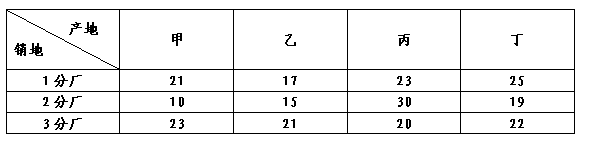
问（1）应该如何安排运输方案，使得总运费为最小？
（2）如果二分厂的产量从400箱提高到600箱，那么应如何安排运输方案，使得总运费最小？

八、医护：某乡镇医院接到一个求助电话，该乡镇一个比较偏远的村庄发生事故，需要紧急救援。上级领导要求该医院：派12名医护人员前往救援，并且要求医护人员在3小时内赶到，该乡镇距离医院40公里。该医院只有1辆汽车，连同司机一次最多拉5人（司机不是医护人员），汽车的速度为60公里/小时,试研究以下问题：

(1)一次一次接送，12名医护人员能否全部按时赶到？

(2)为了节省时间，在汽车拉4人走的时候，其余医护人员步行往前赶，这种方式能否赶到？假定人步行的速度为5公里/小时。

(3)在没有其它辅助条件的前提下，有没有更快、更保险的方案？

九、机械：某厂拥有4台磨床、两台立式钻床、3台卧式钻床、一台镗床和一台刨床，用以生产7种产品，记作P1至P7。工厂收益规定作产品售价减去原材料费用之剩余。每种产品单件的收益及所需各机床的加工工时（以小时计）列于表1，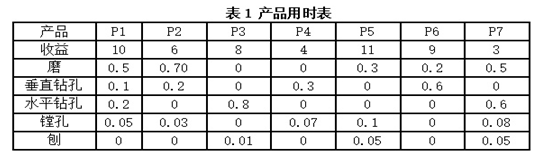

本月（一月）和随后的5个月中，下列机床停工维修：

    一月    磨床一台

        二月   卧式钻床2台

        三月   镗床一台

        四月   立式钻床1台

        五月   磨床一台，立式钻床一台上台下

        六月   刨床一台，卧式钻床1台

各种产品各月份的市场容量如表2：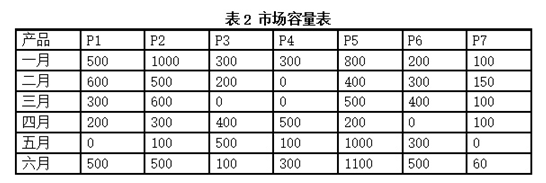

每种产品存货量最多可到100件。存费每件每月为0.5。现在无存货。要求到6月底每种产品有存货50件。工厂每周工作6天，每天2班，每班8小时。不需要考虑排队等待加工的问题。

1、为使收益最大，工厂应如何安排各月份各种产品的产量？考虑价格的某种变化及引入新机床对计划和收益的影响。

注意，可假设每月仅有24个工作日。

2、在工厂计划问题中，各台机床的停工维修不是如问题1那样规定3月份，而是选择最合适的月份维修。除了磨床外，每台机床在这个月中的一个月必须停工维修；6个月中4台磨床只有2台需要维修。扩展工厂计划模型，以使可作上述灵活安排维修时间的决策。停工时间的这种灵活性价值如何？

十、车库的车位停车设计问题：近几年我国居民活水平有了显著提高，我校有越来越多的教师购置了汽车，为了解决停车问题，在图书馆前面造了一个地下车库。车库面积有限，问题是如何利用车库高效地停车，即在保证安全的情况下，尽可能多地停车。为简单起见，我们假设该车库是一个100*100的正方形，见下图:

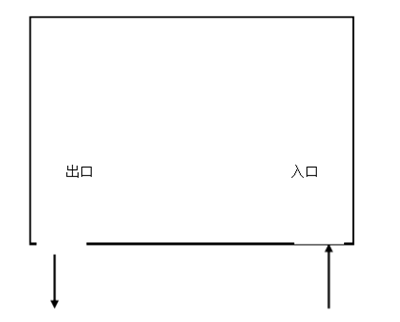
教师的车都是标准的轿车2x3米,车的最小转弯半径为４米，试设计一个最佳停车方案（只考虑平面）。