寻找社团结构的方法

基于网络拓扑结构

GN algorithm based on edge betweenness： M. Girvan, M. E. J. Newman PNAS  99 7821(2002)

Spectral analysis；  L. Donetti, M. A. Munoz J. Stat. Mech. (2004) P10012

基于网络上的动力学

Potts Model；J. Reichardt, S. Bornhold, Phys Rev Lett. 93 (2004) 218701

Random Walk：M.Latapy, P.Pons，cond-mat/0412368 ; H. Zhou PRE.67.041908

Circuits：F. Wu, B.A. Huberman, Eur. Phys. J. B 38 (2004) 331

Q函数优化

Extremal Optimization：J. Duch  A. Arenas, Phys Rev E. 72 (2005) 02710

Newman’s fast algorithm； M. E. J. Newman, Phys Rev E. 69 (2004) 066133

GN算法

●Girvan和Newman提出的分裂算法已经成为探索网络社团结构的一种经典算法，简称GN算法。 

●由网络中社团的定义可知，所谓社团就是指其内部顶点的连接稠密，而与其他社团内的顶点连接稀疏。这就意味着社团与社团之间存在联系的通道比较少，并且要想从一个社团到另一个社团，至少要通过这些通道中的一条。如果能找到这些重要的通道，并将它们移除，那么网络就自然而然的分成了各个社团。 

●用最短路径边介数标记每条边对连通性的重要程度。

●最短路径边介数的定义为：找出每对顶点间的最短路径，计算每条边被多少条最短路径通过，这个值就是这条边的最短路径边介数。

●GN算法的具体过程：

⑴计算网络中各条边的边介数；

⑵找出边介数最大的边，并将它移除（如果最大边介数的边不唯一，那么既可以随机挑选一条边断开也可以将这些边同时断开）；

⑶重新计算网络中剩余各条边的边介数；

⑷重复第⑵、⑶步，直到网络中所有的边都被移除。

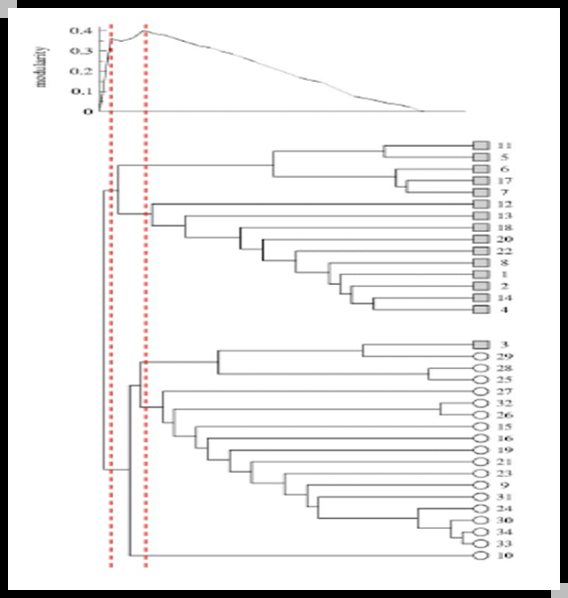
GN算法与Q值

    最优社团划分

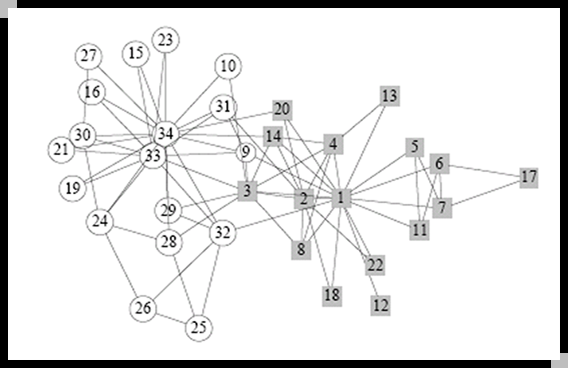
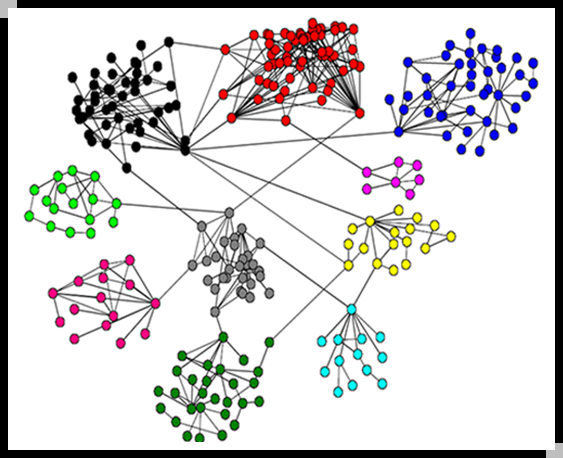
检验算法的网络

●  人工网络                                        GN Benchmark                 LFR benchmark

●  一些实证网络

检验算法的一些实际网络

空手道俱乐部网

科学家合作网

美国大学足球赛季网

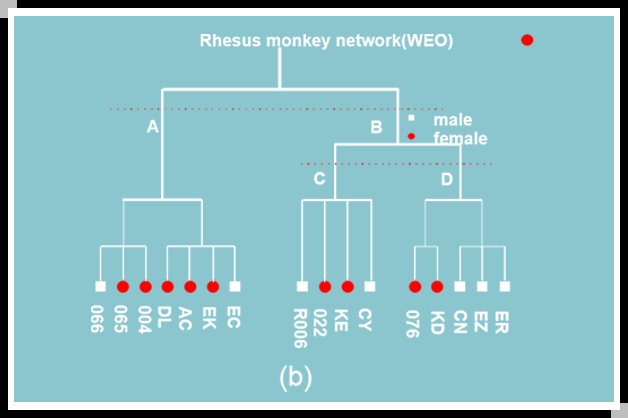
Rhesus猴子网

经济物理学科学家合作网