 社团结构的描述性定义
社团结构的描述性定义
 Community structure(社团结构)
Community structure(社团结构)
is the groups of network vertices. Within these groups there have dense internal links, but between groups there are fewer edges.
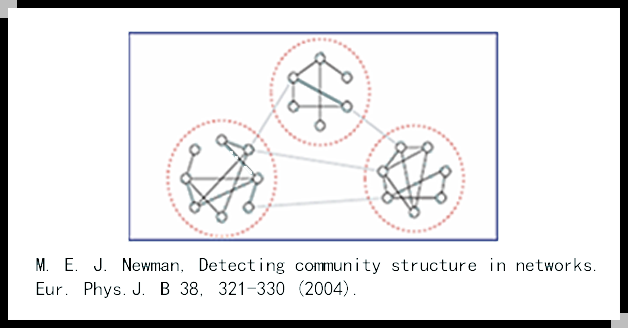
 Community Structures
Community Structures
社团内部连接紧密,社团之间连接相对稀疏。
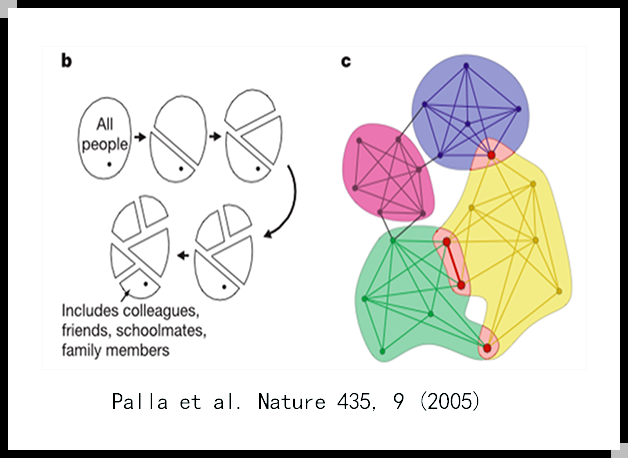
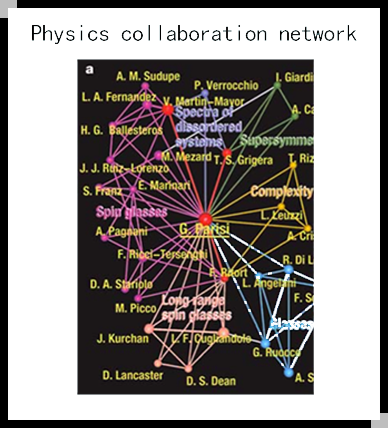
 Santa Fe研究所的科学家合作网
Santa Fe研究所的科学家合作网
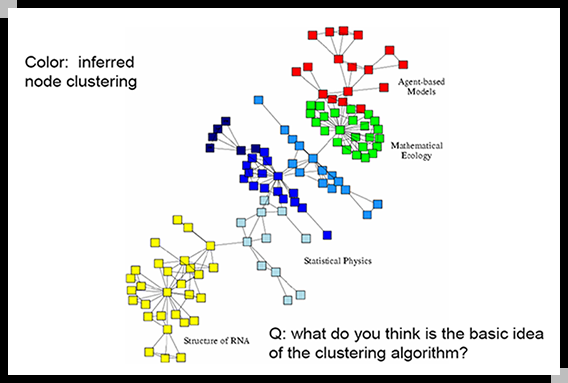
 社团结构的数学描述
社团结构的数学描述
● Clique - Complete graph
● k-core - subgraph in which each node is adjacent to at least a minimum number, k, of the other nodes in the subgraph.
● K-Clique Community
● LS-Set
An LS-set is a set of nodes such that each of its proper subsets has more ties to its complement within the set than outside.
 社团结构的比较性定义
社团结构的比较性定义


 Q函数
Q函数
Girvan和Newman定义模块化来衡量社团划分的优劣。
用Q函数衡量模块化
假设网络已经被划分出集团结构,ci表示顶点i所属的社团,则网络中社团内部连边所占的比例可以表示成:

对于社团结构固定,每个顶点的度值固定,边随机连接的网络,i、j两点存在连边的可能性为

 则Q函数为
则Q函数为
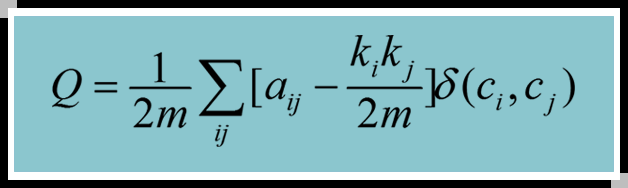
其含义是:网络中连接社团内部顶点间的边的比例与拥有相同社团结构但是顶点间随机连接的网络中连接社团内部顶点间的边的比例的期望值的差值。
如果与随机连接得到的网络没有差别,则说明这种社团结构并不显著。Q函数数值较大时,说明网络的这种社团划分是显著的。


