砂堆模型和自组织临界性

砂堆模型与自组织临界性

Self — Organized Criticality

     1987 年，P. Bak、汤超（C. Tang）和 K. Wiesenfeld 对砂堆模型（Sandpile Model，BTW模型）进行了深入研究，提出了自组织临界性（Self — Organized Criticality，SOC）的概念。现在，SOC 已经成为当代非线性科学的一个重要领域。

SOC 理论的奠基人

        Per Bak （1947—2002）

丹麦物理学家、  哥本哈根大学教授、美国 Brookhaven 研究所教授, 自组织临界（SOC）理论的提出者。Pioneer in the physics of complex systems, and discoverer of self-organized criticality  （Nature, 2002）

汤超（Chao Tang） 

中国科技大学少年班毕业生，美国芝加哥大学博士。1987年与其导师 P.Bak 等共同提出自组织临界（SOC）理论，作出了开创性贡献。现任美国 NEC 研究院的高级研究员、北京大学理论生物学中心主任、中国科学院交叉科学中心特聘教授。  

Kurt  Wiesenfeld

美国加州伯克利大学博士、美国乔治亚州工学院教授，1987年与 P.Bak 、汤超共同提出自组织临界（SOC）理论，作出了开创性贡献。

砂堆模型

Sandpile Model

砂堆模型 —— 计算机模拟

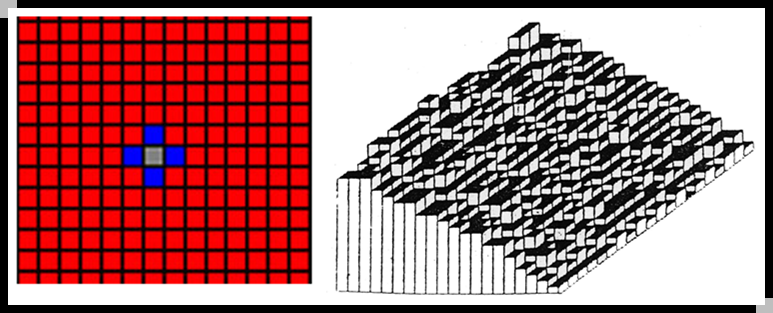
砂堆模型 —— 演化规则

随机地加一粒沙子：

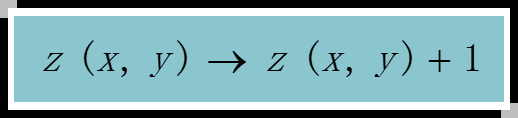
当达到阈值 4 时：

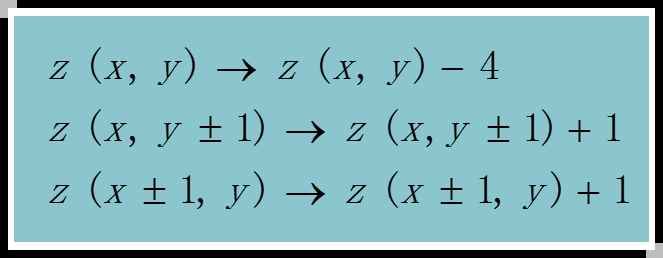
这是一种二维的元胞自动机， 其非线性体现在达到阈值后的释放和再分配上。

砂堆模型 —— 演化规则

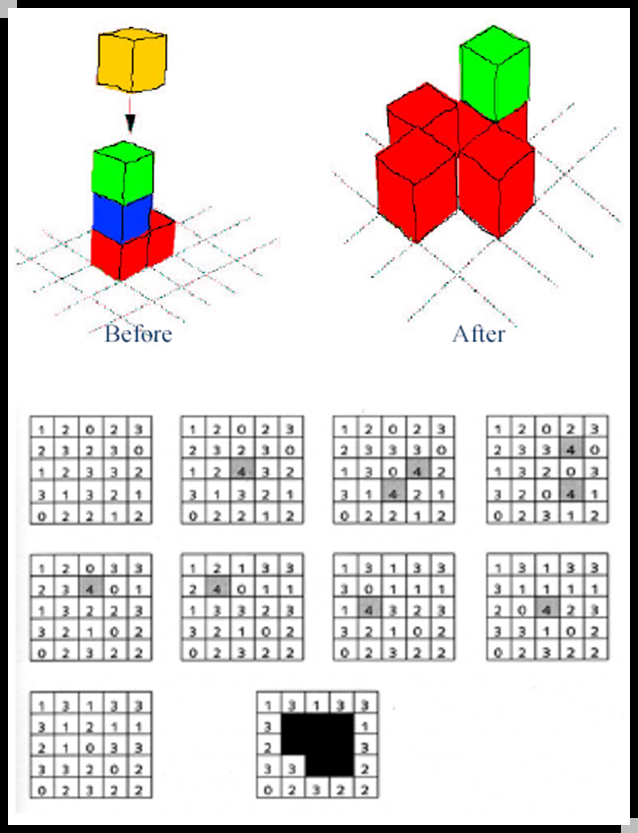
“雪崩”的发展过程

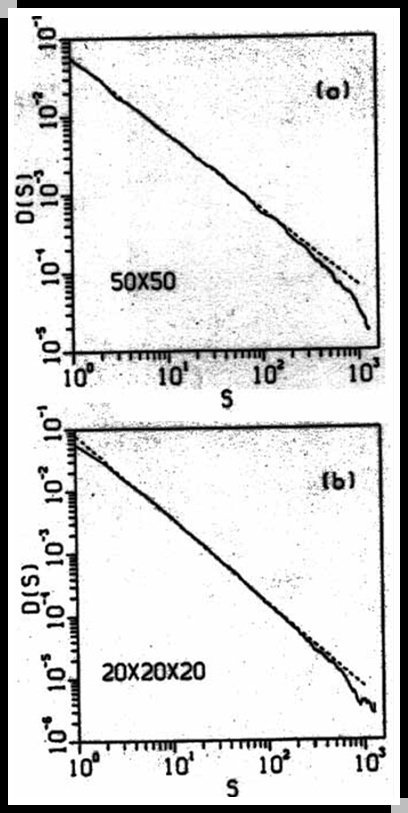
砂堆模型—— 雪崩大小的分布

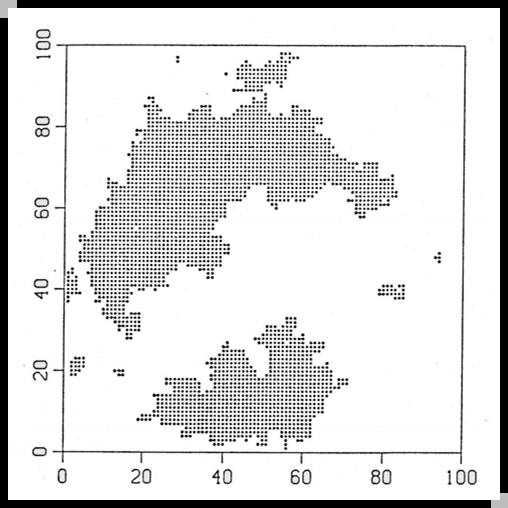
雪崩的大小呈幂律分布，在双对数坐标图上形成直线。

自然界和社会中的临界自组织现象

●   地震

●   生物群落（如：蚁群）

●   流行病传播

●   森林火灾

●   城市交通

●   Internet 

●   1 / f  噪声

     … …     … … 

SOC 的各种模型

●  砂堆模型（sandpile  model，BTW 模型）

●   米堆模型（ricepile  model）

●   扩散置限凝聚（DLA）模型

●   电介质击穿模型（DBM）

●   纤维束断裂模型

●   弹簧 — 滑块模型（OFC 模型）

●   森林火灾模型（forest  fire  model，FF 模型）

●   城市交通模型

●   Bak—Sneppen 模型（B-S 模型）

Per Bak.	Stephen Wolfram.
How Nature Works?  Springer  1996	A New Kind of Science. Wolfram Media, 2002.