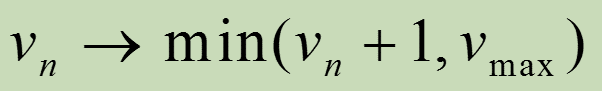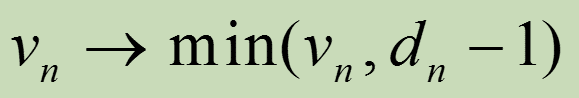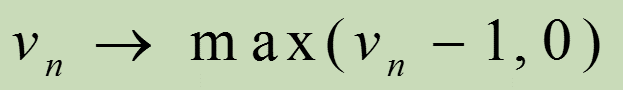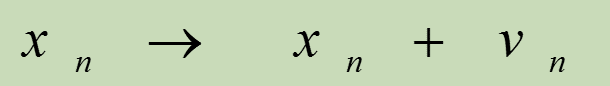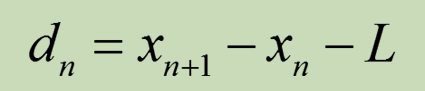元胞自动机交通流模型

特别注意：第184号规则

车辆行驶规则为：黑色元胞表示被一辆车占据，白色表示无车，若前方格子有车，则停止。若前方为空，则前进一格。

第184号规则的结构演化时空图

交通流的NS 模型

在第184号规则的基础上，1992年，德国学者Nagel和Schreckenberg提出了一维交通流CA模型，即，NS 模型

Nagel and Schreckenberg. A Cellular automaton model for freeway traffie．Journal of Physics(France)，1992 

NS模型是一个随机CA交通流模型，每辆车的状态都由它的速度和位置所表示，其状态按照以下演化规则并行更新 ： 

a）加速过程：

b）安全刹车过程：

c）随机慢化过程：（以随机慢化概率p）

d）位置更新：

其中：L---车辆长度

例：设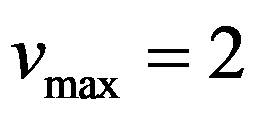
a）加速过程
b）安全刹车过程
c）随机慢化过程（以随机慢化概率p）
d）位置更新

高速公路自发形成的堵塞——幽灵堵塞（ghost jam）、时走时停（stop-and-go wave）

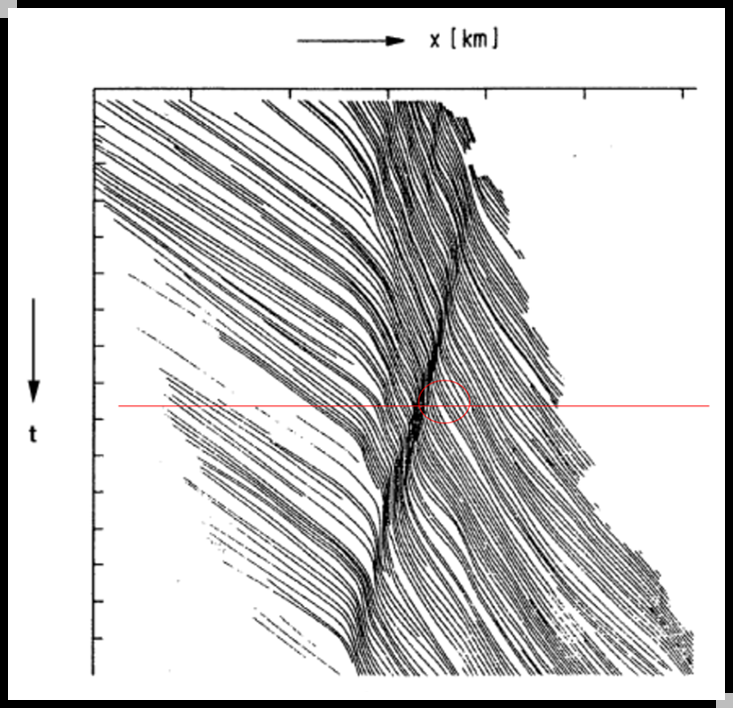
航拍图，J.Treiterer，1975年

交通流CA模型的主要优点：

模型简单，特别易于在计算机上实现。

能够再现各种复杂的交通现象，反映交通流特性。在模拟过程中人们通过考察元胞状态的变化，不仅可以得到每一辆车在任意时刻的速度、位移以及车头时距等参数描述交通流的微观特性，还可以得到平均速度、密度、流量等参数，呈现交通流的宏观特性。

能够再现单车道、多车道以及路网的交通流建模；机动车和非机动车交通流的建模。