初等元胞自动机

20世纪50年代，John  von  Neumann 最早提出；

(von Neumann,J.1963，collected works, edited by A.H.Taub)

1970年，John Conway 提出生命游戏

(Conway, J. (1970). In M. Gardner, (Ed.), Scientific American, 223(4), pp. 120-123.)

1983年，Stephen Wolfram 初等元胞自动机

(Stephen Wolfram. Reviews of Modern Physics,1983,Vol.55.

Stephen Wolfram. Nature,1984,Vol.311)

1986年至今，理论及应用

任意格子i有两种状态，且状态是随时间变化。

为格子i在t时刻的状态：

                

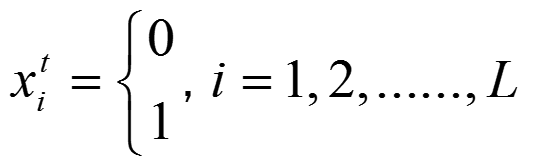
状态演化方程

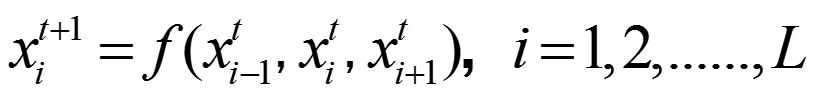
周期边界

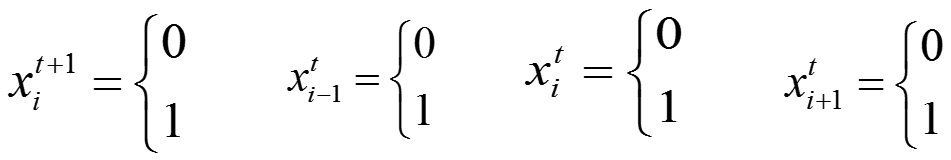
例题:按规则90 从初始状态0011011010演化

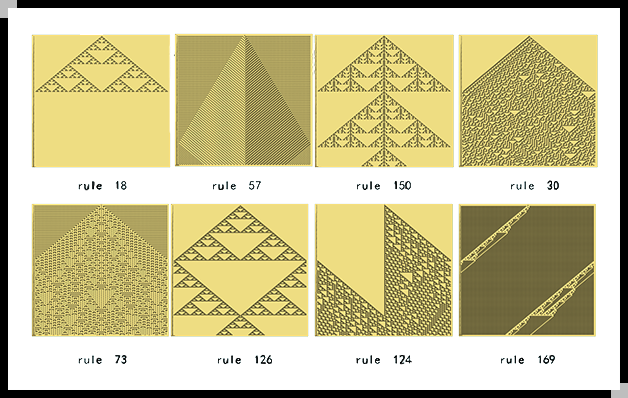
0——白色    1——黑色     L=100

初值取第50个格子为1，对每个规则演化100步。以下为部分规则下的结构时空图。