现代混沌科学的诞生

Lorenz系统——大气动力学

美国麻省理工学院教授洛伦兹(Edward N. Lorenz)

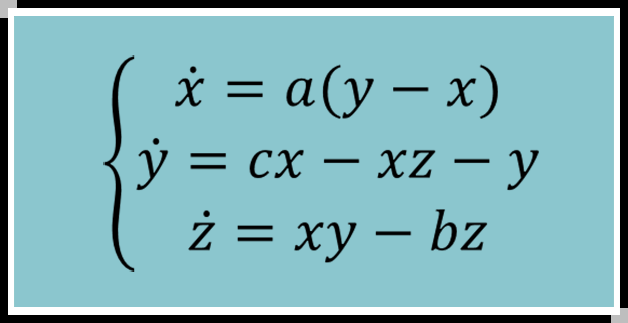
1961年的某一天，洛伦兹在办公室里把一个数据输入到一台及其缓慢的Royal McBee计算机，企图重复验证上一次的计算结果。

他知道这需要等一个多小时，便踱进了旁边的一间小小咖啡馆……

Lorenz的意外发现

当他回到自己的工作室时惊讶地发现：这次的结果与上次的结果在开始时相同，但到后来却面目全非：

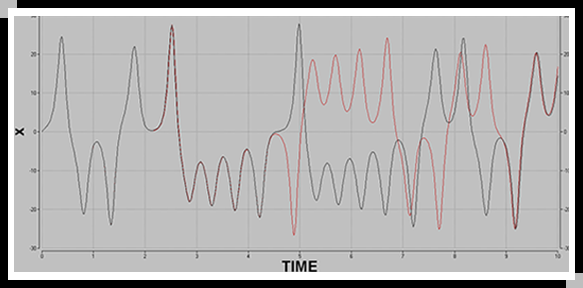
在第一次计算中，他输入的初始值是0.506127

在第二次计算中，他图省事，输入了0.506

由于“系统对初值的高度敏感”，一个微小的初始误差随着反复迭代计算会酿成结果的巨大差异

Lorenz系统

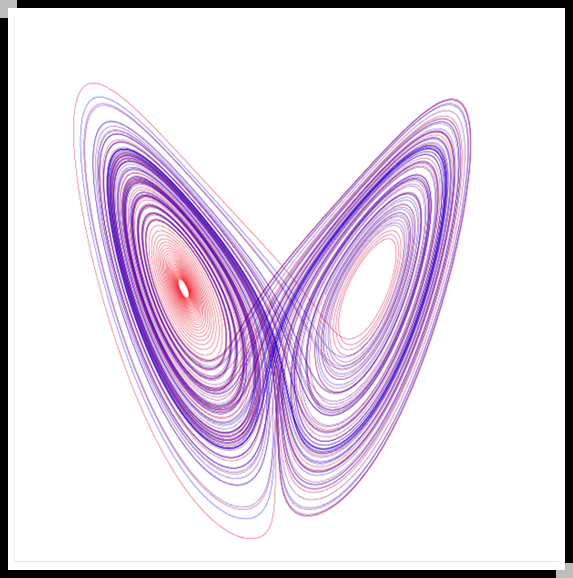
a=10, b=8/3, c=28                吸引子 Attractor                -不发散               -不收敛               -非周期

E. N. Lorenz, Deterministic Nonperiodic Flow, Journal of the Atmospheric Sciences, 20:130-141,1963

他的结论是：由于天气观测中存在着不明显的不确定性和不完全性，非常长期的天气预报是不可能的。

现代混沌科学的奠基性论文

“Does the flap of a butterfly’s wing in Brazil set off a tornado in Texas?”                                                                                                                            —E. N. Lorenz

  在巴西的一只蝴蝶拍打一下翅膀，会在德克萨斯引发一场龙卷风吗？

混沌运动

非线性确定性系统中, 由于系统内部非线性相互作用而产生的一种非周期行为。

对初始条件的敏感性 该特点形象的称为“蝴蝶效应”，这一性质使确定性系统表现出随机性，系统地长期预测不可能；

有界性 混沌系统的轨道一直在被称之为混沌吸引子的有界区域内运动。

遍历性 混沌系统的运动是遍历的。如果在某一时刻，轨道通过吸引子内部的某一点的某一邻域，那么轨道还会再次通过该邻域。