动力系统定性分析
上一节
下一节
 动力系统的定性方法
动力系统的定性方法
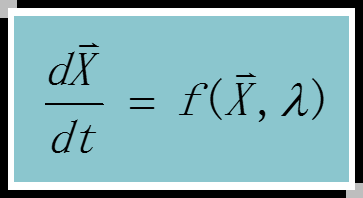
 从质点动力学谈起
从质点动力学谈起
 质点的运动
质点的运动
| 牛顿运动定律 |
第一定律:惯性定律 第二定律:F=ma 第三定律:作用力与反作用力定律 |
 开普勒问题
开普勒问题
 开普勒问题——二体问题
开普勒问题——二体问题
1710年由瑞士数学家伯努利首先解决
如果两个物体之间的相互作用力为万有引力,那么当你站在一个质点上观察另一个质点的运动时,另一个质点的轨道一定是直线、抛物线、椭圆、或者双曲线的一支。
 拉普拉斯决定论
拉普拉斯决定论
“我们可以认为宇宙的现在是由它的过去来决定的;现在也是决定未来的原因。如果有一位智者在某一时刻获知了自然界一切物体的位置和相互作用力,并且他具有超常的数据分析能力,那么他就可以把宇宙这个最庞大的物体直至到原子这个最细微的颗粒全都囊括到一个公式中去。对于这位智者来说,没有什么东西是不确定的——宇宙的未来会像它的过去一样完全呈现在他的眼前。”
——Marquis Pierre Simon de Laplace (1984)
 三体问题
三体问题
 太阳、地球和月亮
太阳、地球和月亮

三体问题是天体力学中的基本力学模型,研究三个可视为质点的天体在相互引力作用下的运动规律。这三个天体的质量、初始位置和初始速度都是任意的。
1887年,瑞典国王奥斯卡(Oskar,II)悬赏,征求太阳系稳定性问题的解答,期望解决天体力学中的N体问题。 |
|
彭加莱(Henri Poincaré) 以他在三体问题的研究成果获得大奖。 |
|
 动力系统定性理论
动力系统定性理论
 关心系统演化在t→∞时的定性行为
关心系统演化在t→∞时的定性行为
区域无穷。 不动点。 周期解。
除以上3种以外的其他行为。




