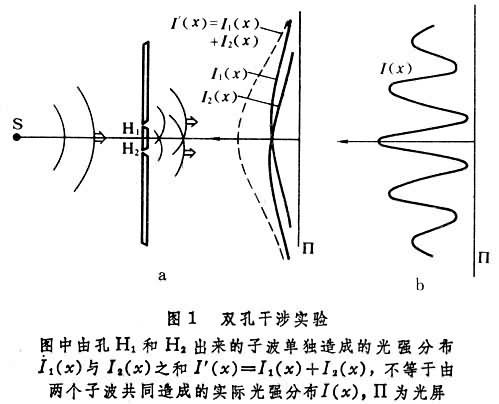
若干个光波（成员波）相遇时产生的光强分布不等于由各个成员波单独造成的光强分布之和，而出现明暗相间的现象。例如在杨氏双孔干涉（见杨氏干涉实验）中，由每一小孔H1或H2出来的子波就是一个成员波，当孔甚小时，由孔H1出来的成员波单独造成的光强分布 I1(x)在相当大的范围内大致是均匀的；单由从孔H2出来的成员波造成的光强分布I2(x)亦如此。二者之和仍为大致均匀的分布。而由两个成员波共同造成的光强分布I(x)，则明暗随位置x的变化十分显著，显然不等于I1(x)+l2(x)。

每个成员波单独造成大致均匀的光强分布，这相当于要求各成员波本身皆没有明显的衍射，因为衍射也会造成明暗相间的条纹（见光的衍射）。所以，当若干成员波在空间某一区域相遇而发生干涉时，应该是指在该区域中可以不考虑每个成员波的衍射。

应注意，前面所说的光强并不是光场强度（正比于振幅平方）的瞬时值，而是在某一段时间间隔 Δt 内光场强度的平均值或积分值；Δt 的长短视检测手段或装置的性能而定。例如，人眼观察时，Δt 就是视觉暂留时间；用胶片拍摄时，Δt 则为曝光时间。

干涉现象通常表现为光场强度在空间作相当稳定的明暗相间条纹分布；有时则表现为，当干涉装置的某一参量随时间改变时，在某一固定点处接收到的光强按一定规律作强弱交替的变化。

光的干涉现象的发现在历史上对于由光的微粒说到光的波动说的演进起了不可磨灭的作用。1801年，T.杨提出了干涉原理并首先做出了双狭缝干涉实验，同时还对薄膜形成的彩色作了解释。1811年，D.F.J.阿喇戈首先研究了偏振光的干涉现象。现代，光的干涉已经广泛地用于精密计量、天文观测、光弹性应力分析、光学精密加工中的自动控制等许多领域。

综述

只有两列光波的频率相同，相位差恒定，振动方向一致的相干光源，才能产生光的干涉。由两个普通独立光源发出的光，不可能具有相同的频率，更不可能存在固定的相差，因此，不能产生干涉现象。

具体方法

为使合成波场的光强分布在一段时间间隔Δt内稳定，要求：①各成员波的频率v（因而波长λ ）相同；②任两成员波的初位相之差在Δt内保持不变。条件②意味着，若干个通常独立发光的光源，即使它们发出相同频率的光，这些光相遇时也不会出现干涉现象。原因在于：通常光源发出的光是初位相作无规分布的大量波列，每一波列持续的时间不超过10秒的数量级，就是说，每隔10秒左右，波的初位相就要作一次随机的改变。而且，任何两个独立光源发出波列的初位相又是统计无关的。由此可以想象，当这些独立光源发出的波相遇时，只在极其短暂的时间内产生一幅确定的条纹图样，而每过10秒左右，就换成另一幅图样，迄今尚无任何检测或记录装置能够跟上如此急剧的变化，因而观测到的乃是上述大量图样的平均效果，即均匀的光强分布而非明暗相间的条纹。不过，近代特制的激光器已经做到发出的波列长达数十公里，亦即波列持续时间为10秒的数量级。因此，可以说，若采用时间分辨本领Δt比10秒更短的检测器（这样的装置是可以做到的），则两个同频率的独立激光器发出的光波的干涉，也是能够观察到的。另外，以双波干涉为例还要求：③两波的振幅不得相差悬殊；④在叠加点两波的偏振面须大体一致。

当条件③不满足时，原则上虽然仍能产生干涉条纹，但条纹之明暗区别甚微，干涉现象很不明显。条件④要求之所以必要是因为，当两个光波的偏振面相互垂直时，无论二者有任何值的固定位相差，合成场的光强都是同一数值，不会表现出明暗交替（欲观察明暗交替，须借助于偏振元件）。

以上四点即为通常所说的相干条件。满足这些条件的两个或多个光源或光波，称为相干光源或相干光波。