一、直线的投影特性

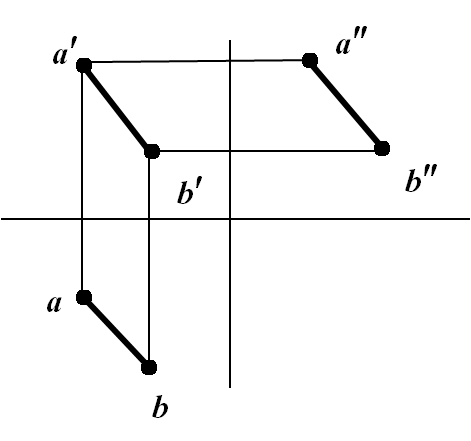
     规定:直线的投影若可见，

     用粗实现画；若不可见，

     用细虚线画。

⒈ 直线对一个投影面的投影特性

⒉ 直线在三个投影面中的投影特性

二、投影面平行线

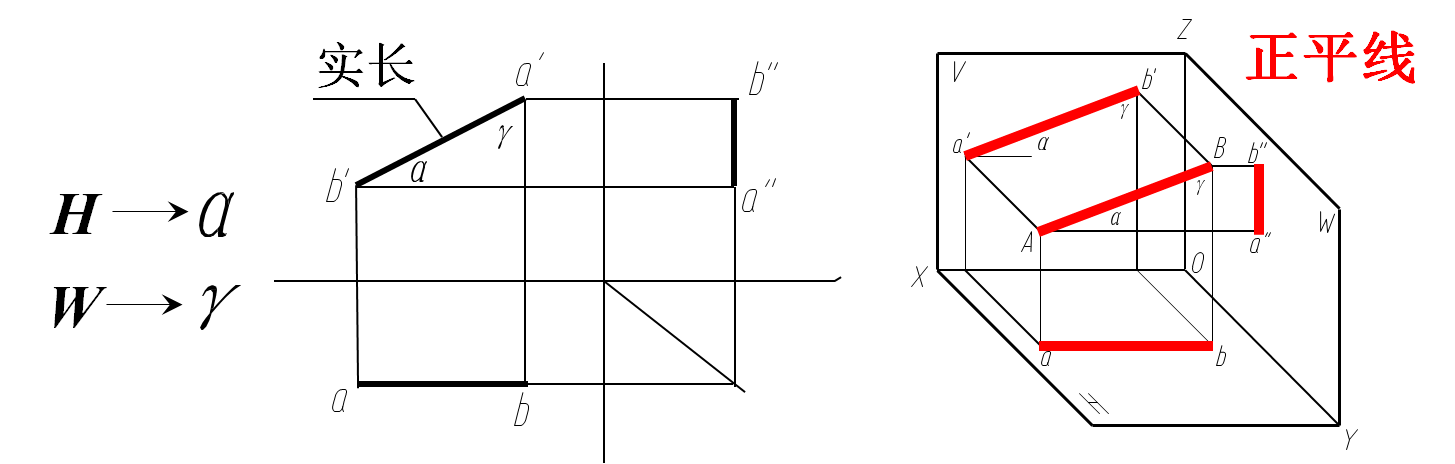
投影特性：① 正面的投影反映实长，与X轴的夹角反映α角、与Z轴的夹角反映γ角。

          ② 另两个投影面上的投影平行于相应的投影轴。

投影特性：① 水平投影反映实长，与X轴的夹角反映β角、与Y轴的夹角反映γ角。

          ② 另两个投影面上的投影平行于相应的投影轴。

投影特性：① 侧面的投影反映实长，与Y轴的夹角反映α角、与Z轴的夹角反映β角。

          ② 另两个投影面上的投影平行于相应的投影轴。

投影特性：① 在其平行的那个投影面上的投影反映实长，并反映直线与另两投影面的倾角。

          ② 另两个投影面上的投影平行于相应的投影轴。

三、投影面垂直线

投影特性：① 正面投影积聚为一点。

          ② 另两面投影垂直于相应的投影轴且反映直线的实长。

投影特性：① 水平投影积聚为一点。

          ② 另两面投影垂直于相应的投影轴且反映直线的实长。

投影特性：① 侧面投影积聚为一点。

          ② 另两面投影垂直于相应的投影轴且反映直线的实长。

四、一般位置直线

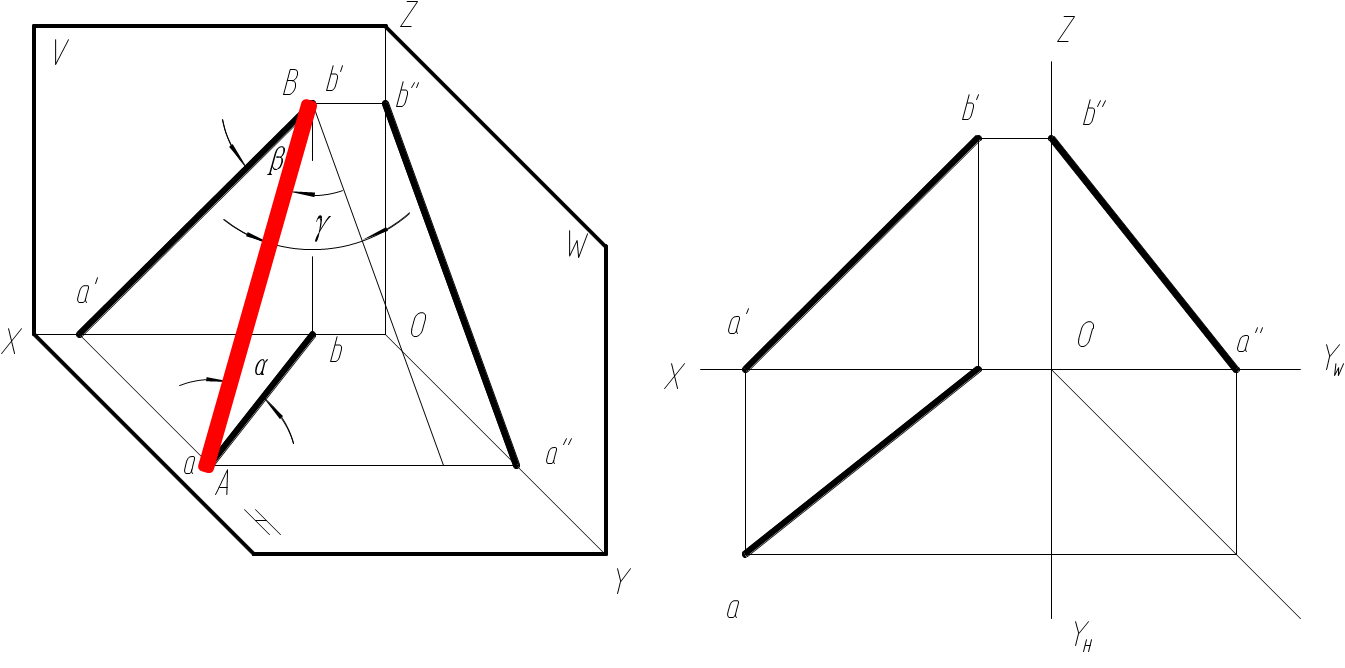
投影特性：三面投影均不反映直线的实长，也不反映直线对投影面的倾角。

五、直线上的点

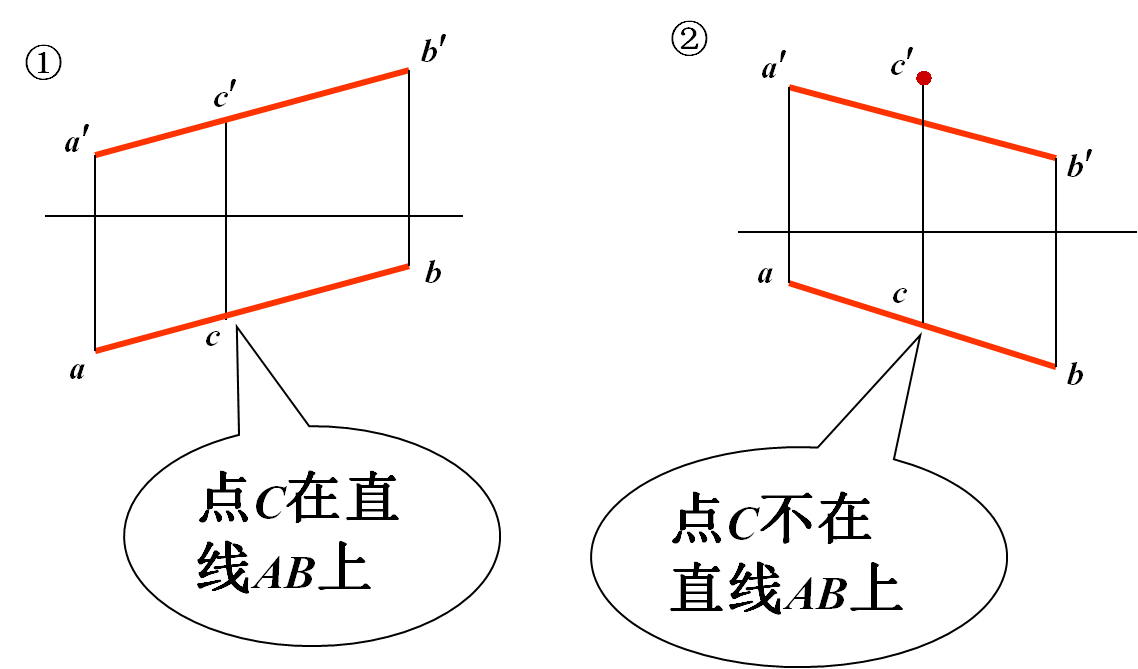
若点在直线上,则点的投影必在直线的同名投影上。

反之，点的各个投影在直线的同面投影上，则该点一定在直线上。 

直线上点分割直线段成定比，则分割线段的各个同面投影之比等于其线段之比。　

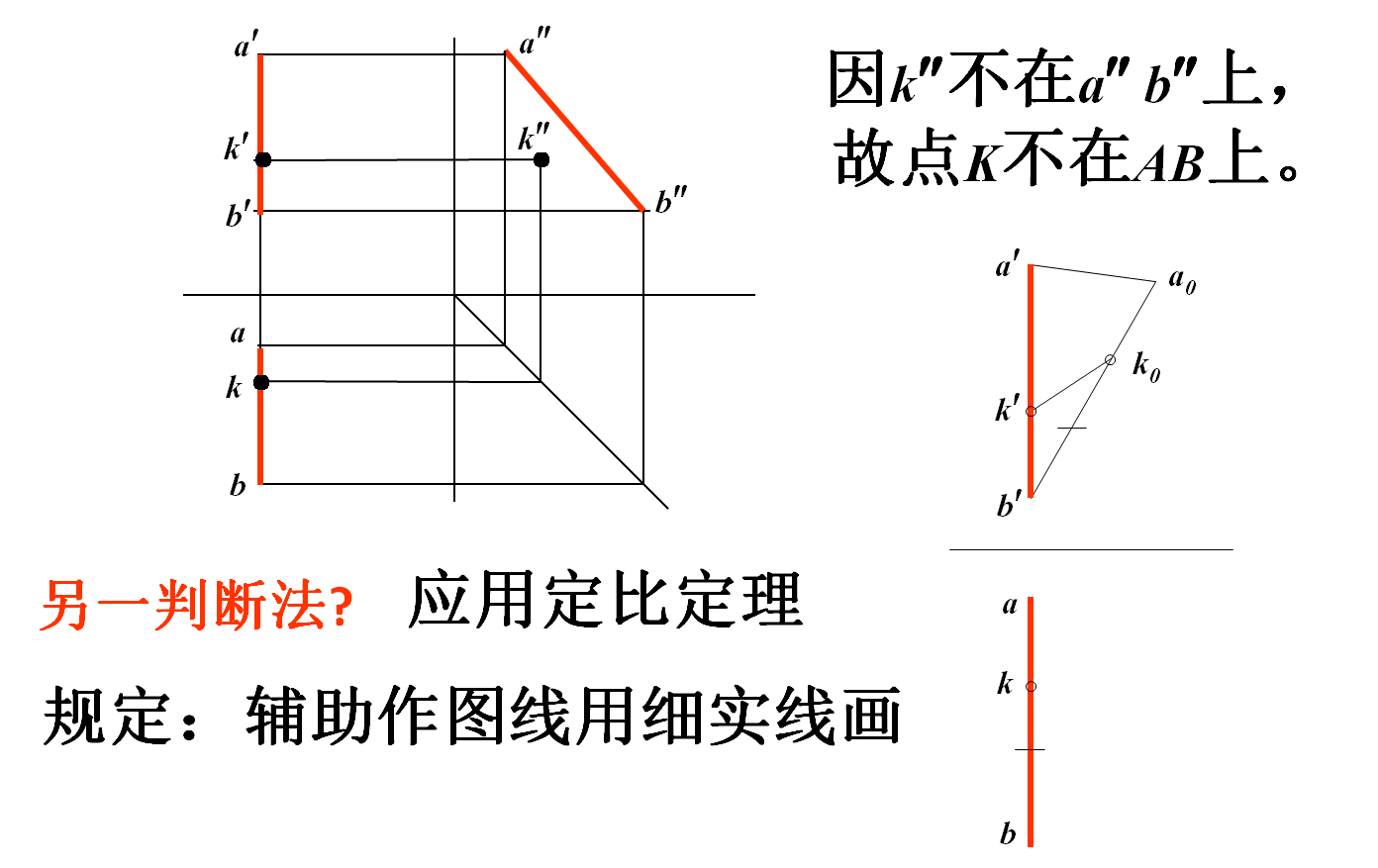
若点的投影有一个不在直线的同名投影上， 则该点必不在此直线上。

例2  判断点C是否在线段AB上。

例3  判断点K是否在线段AB上。

六、两直线的相对位置

空间两直线的相对位置分为：平行、相交、交叉。

⒈ 两直线平行

     投影特性：空间两直线平行，则其各同名投影必相互平行，反之亦然。

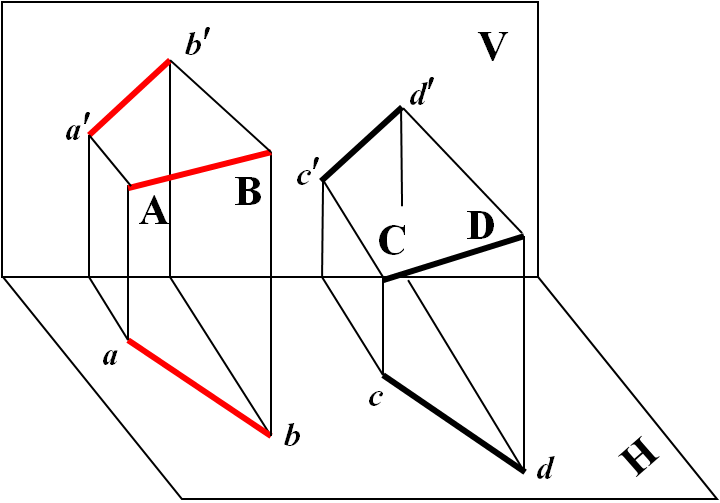
例4  判断图中两条直线是否平行。

   

   对于一般位置直线，只要有两个同名投影互相平行，

空间两直线就平行。

AB//CD

例5  判断图中两条直线是否平行。

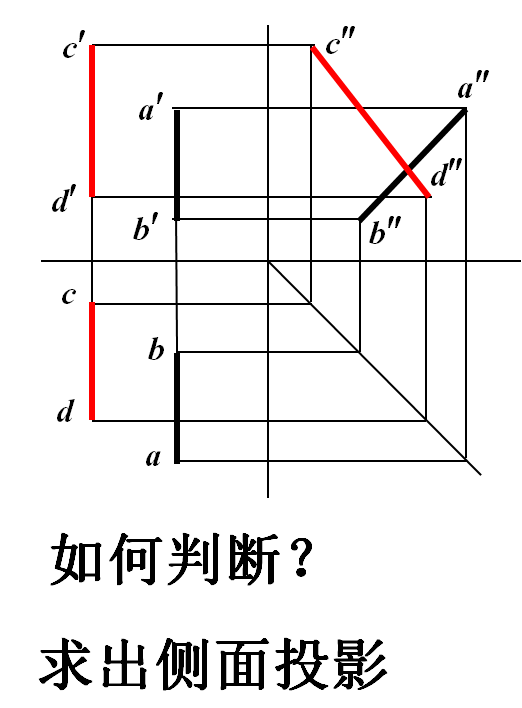
   对于特殊位置直线，只有两个同名投影互相平行，

空间直线不一定平行。

   求出侧面投影后可知：

   AB与CD不平行。

⒉ 两直线相交

判别方法：若空间两直线相交，则其同名投影必相交，且交点的投影必符合空间一点的投影规律。

例6  过C点作水平线CD与AB相交。

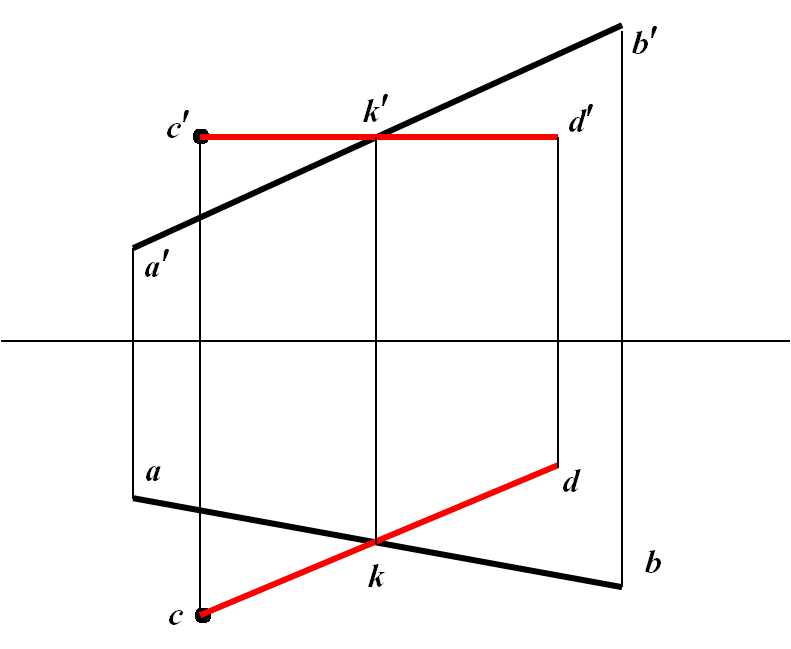
规定：对求作的结果，若可见，用粗实线画；若不可见，用细虚线画。

⒊ 两直线交叉

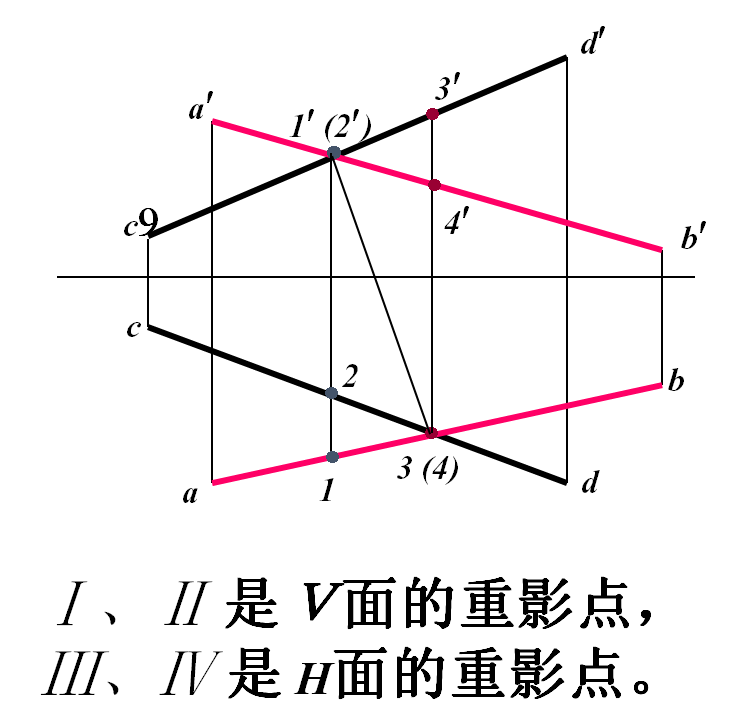
     两直线相交吗？

     投影特性：同名投影可能相交，但 “交点”不

符合空间一个点的投影规律。

  “交点”是两直线上的一对重影点的投影，

用其可帮助判断两直线的空间位置。

例5  判断图中两条直线是否平行。

                求出侧面投影               AB与CD不平行。