2.9 Matlab在离散时间信号和系统分析中的应用

.

%单位冲击序列 

function[x,n]=impseq(n0,n1,n2)

n=[n1:n2];

x=[(n-n0)==0];

stem(n,x);

%单位阶跃序列

function[x,n]=stepseq(n0,n1,n2)

n=[n1:n2];l x=[(n-n0)>=0];

% 噪声干扰的余弦信号 x(n)=cos(0.04n*PI)+0.2w(n)

n=[0:100];

x=cos(0.04*pi*n)+0.2*randn(size(n));

subplot(2,1,1);plot(n,x);xlabel('n');ylabel('x(n)');

subplot(2,1,2);stem(n,x);xlabel('n');ylabel('x(n)');

2.28 设某因果系统如下列差分方程描述

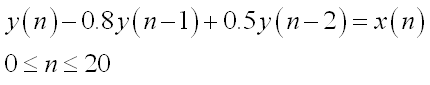
，计算该系统的冲击响应和单位阶跃响应。

解：

%输入差分方程系数

b=[1];a=[1,-0.8,0.5];

%计算冲击响应

x=impseq(0,0,20);n=[0:20];

h=filter(b,a,x);

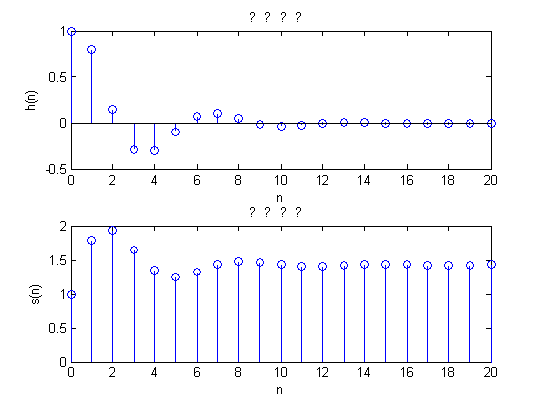
subplot(2,1,1);stem(n,h);title('冲击响应');

xlabel('n');ylabel('h(n)');

%计算阶跃响应

x=stepseq(0,0,20);

s=filter(b,a,x);

subplot(2,1,2);stem(n,s);title('阶跃响应');

xlabel('n');ylabel('s(n)');

%求极点模，判断稳定性

2.29 某因果系统如下列差分方程描述

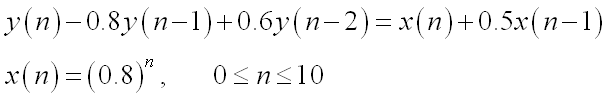
计算该系统的冲击响应和对输入x的响应。

解：

%输入差分方程系数

b=[1,0.5];a=[1,-0.8,0.6];

%计算冲击响应

x=impseq(0,0,20);n=[0:20];

h=filter(b,a,x);

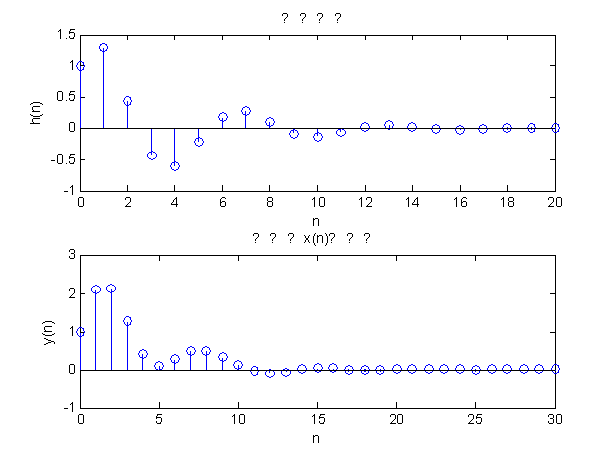
subplot(2,1,1);stem(n,h);title('冲击响应');

xlabel('n');ylabel('h(n)');

%计算对x(n)的响应

n=0:10;x=(0.8).^n;nx=[0:10];nh=[0:20];

y=conv(x,h);ny=length(y);

n=0:ny-1;

subplot(2,1,2);stem(n,y);title('系统对x(n)的响应');

xlabel('n');ylabel('y(n)');

%求极点模，判断稳定性

2.30 设信号

用MatLab计算DTFT，并画图表示。

解：

%计算序列DTFT

%输入序列

n=-1:3;x=1:5;

%在横轴上分点

k=0:500;w=(pi/500)*k;

%计算DTFT

X=x*(exp(-j*pi/500)).^(n'*k);

magX=abs(X);angX=angle(X);

subplot(2,1,1);plot(w/pi,magX);title('幅度响应');grid;

ylabel('幅度');xlabel('以PI为单位的频率');

subplot(2,1,2);plot(w/pi,angX);title('相位响应');grid;

ylabel('相位/\pi');xlabel('以PI为单位的相位');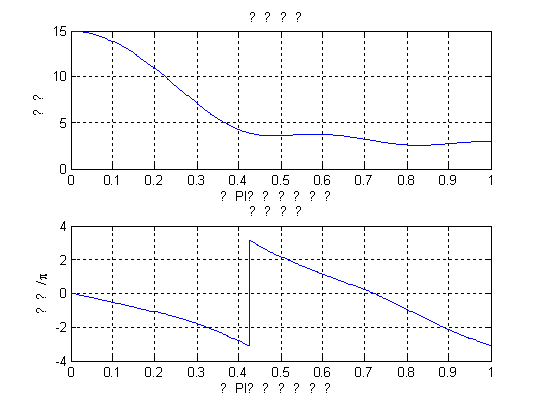

2.32 用Matlab求z变换的反变换

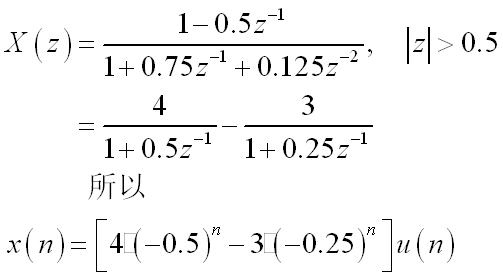
解：

%部分分式法求逆z变换

b=[1,-0.5];a=[1,0.75,0.125];

[R,P,C]=residuez(b,a);

disp('R=');disp(R');

disp('P=');disp(P');

disp('C=');disp(C');

R=

4    -3

P=

-0.5000   -0.2500

C=

>> 

2.33 用Matlab求z变换的反变换

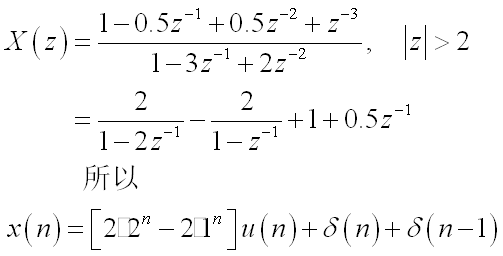
解：

%部分分式法求逆z变换

b=[1,-0.5,0.5,1];

a=[1,-3,2];

[R,P,C]=residuez(b,a);

disp('R=');disp(R');

disp('P=');disp(P');

disp('C=');disp(C');

R=

2    -2

P=

2     1

C=

1.0000

0.5000