2.8  全通系统与最小相位系统

2.8.1全通系统

如果一个系统的幅频响应对所有的

频率都等于1 (或一个常数), 即

则称系统为全通系统。

最简单的全通系统，纯延迟：

一阶全通系统：

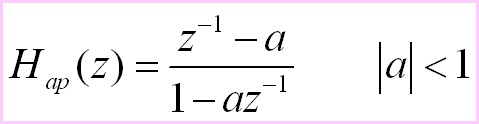
镜像对称

二阶全通系统：

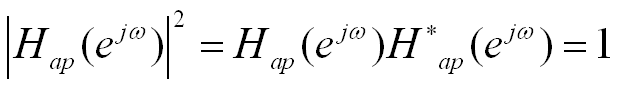
一对位于单位圆内的共轭极点，一对共轭零点和极点以单位圆为镜像对称。

高阶全通系统：

一阶全通系统的相位函数为：

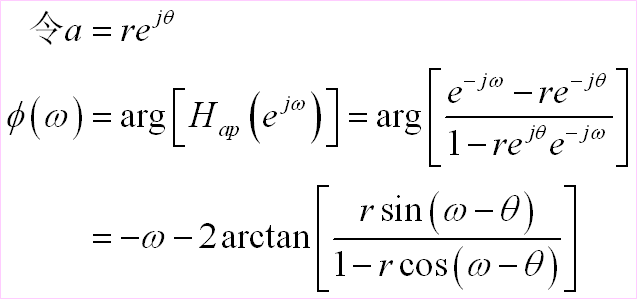
全通系统的特点：

1.是IIR系统(不考虑纯延迟形式）；

2.极点数和零点数相等；

3.极点和零点是以单位圆镜像对称的；

4.极点都在单位圆内,零点都在单位圆外；

5.全通系统的群延迟始终为正值。

全通系统的应用：

IIR系统的无限长，无法对称，即无法作到线性相位。在实际中，可以用一个全通系统和IIR系统相级联，在不改变幅频响应的情况下对相频响应做矫正，使其接近线性相位。

全通系统还广泛应用在系统分析及一些特殊滤波器的设计方面（如功率互补IIR滤波器组）

一阶全通系统

                                        极－零图                                                 幅频

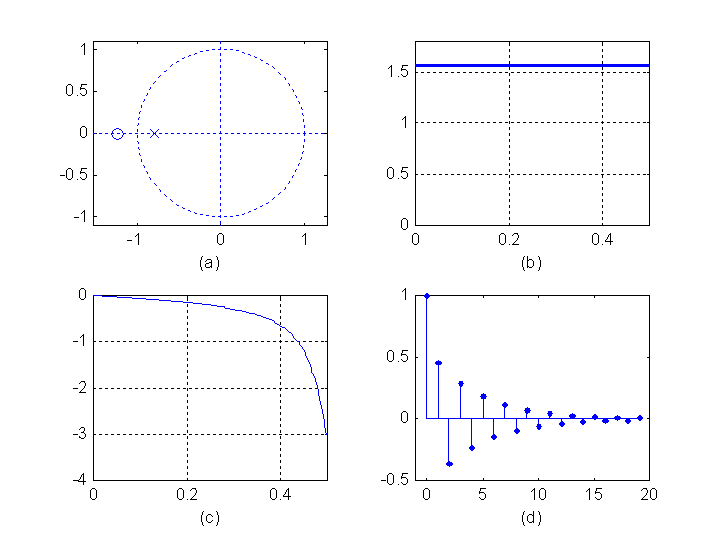
                                            相频                                                    抽样响应

三阶全通系统

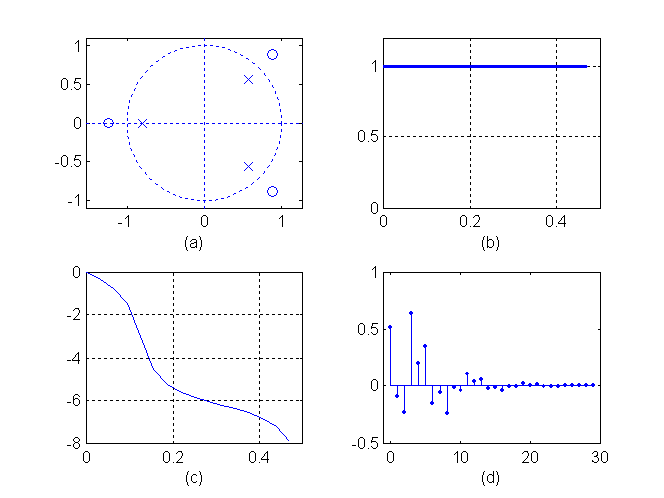
2.8.2最小相位系统

一个离散系统，其极点必须在单位圆内，但对零点没有限制，如果：

1.所有的零点都在单位圆内：最小相位系统；

2.  所有的零点都在单位圆外：最大相位系统；

3. 单位圆内、外都有零点：混合相位系统。

最小相位系统记作

存在条件:存在一个稳定的因果逆系统

定义：稳定因果的系统，其极点、零点均位于单位圆内（上）

对于稳定因果系统，当且仅当其是最小相位系统时, 该系统才有逆系统（Inverse System)。

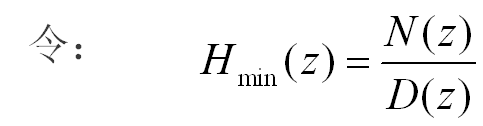
记：

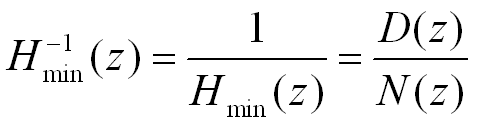
该逆系统是稳定且因果的

例: 三个系统：

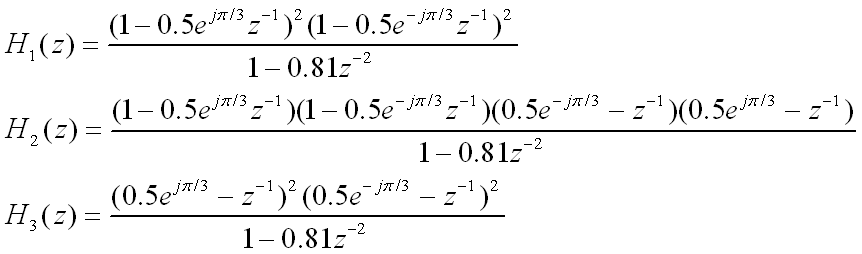
它们具有相同的幅频响应，试判断，那一个是最小相位系统？最大相位系统？混合相位系统？

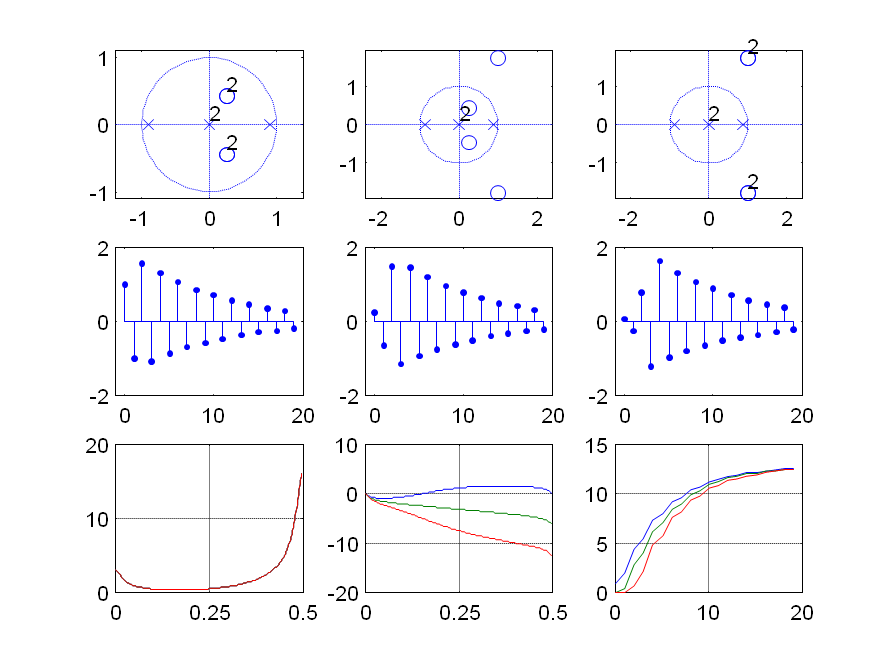
任一非最小相位的因果系统的转移函数均可由一个最小相位系统和一个全通系统级联而成, 即：

由于最小相位系统有着以上特殊的性质，因此有着广泛的应用，特别是在信号的建模与系统辨识方面。要理解，具有相同幅频响应的系统，它们所对应的转移函数可以是不相同的，区别就在于相位（或零点的位置）。

2.8.3 相位延迟和群延迟

假设数字滤波器的传输函数Y(e jω)用下式表示：

幅频特性|Y(ejω)|：

信号通过滤波器后的各频率成分衰减情况。

相频特性.(ω)：

各频率成分通过滤波器后在时间上的延时情况。

设输入信号经过系统后延迟了时间m，则有

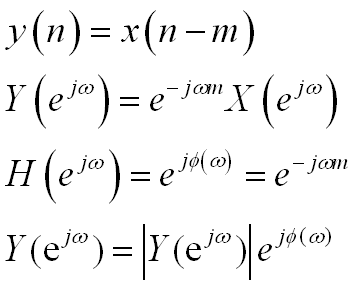
于是

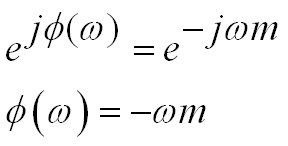
相位延迟定义为

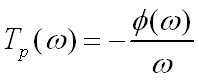
群延迟响应：相位对角频率的导数的负值

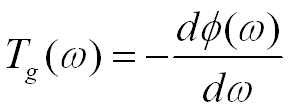
群延迟表示某一频率邻域内的延迟特性，即频率包络的延迟时间。