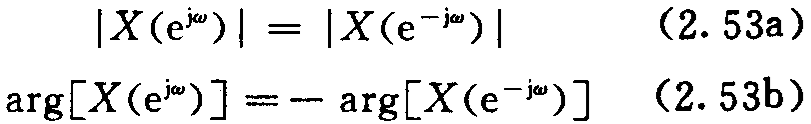2.4.1离散时间信号的傅里叶变换

众所周知，连续时间信号f(t)的傅里叶变换定义为：

而f(jΩ)的傅里叶反变换定义为

类似地，可以把离散时间信号x(n)的傅里叶变换定义为

X(ejω)的傅里叶反变换定义为

在物理意义上，X(ejω)表示序列x(n)的频谱，ω为数字域频率。X(ejω)一般为复数，可用它的实部和虚部表示为

或用幅度和相位表示为

例2．9求下列信号的傅里叶变换

解：

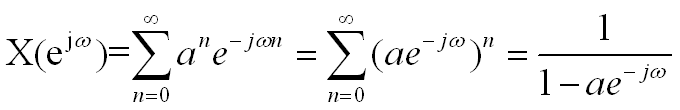
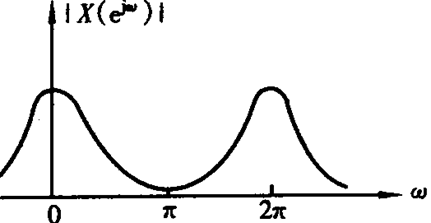
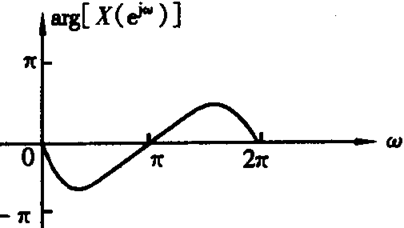
离散时间信号的傅里叶变换具有以下两个特点：

(1)X(ejω)是以2π为周期的ω的连续函数。

(2)当x(n)为实序列时，X(ejω)的幅值| X(ejω) |在0≤ω≤2π区间内是偶对称函数，相位arg[X(ejω)]是奇对称函数。

值得注意的是，式(2. 34a)中右边的级数并不总是收敛的，或者说并不是任何序列x(n)的傅里叶变换都是存在的。

只有当序列x(n)绝对可和，即

时，式(2. 34a)中的级数才是绝对收敛的，或x(n)的傅里叶变换存在。

2.4.2离散时间信号的傅里叶变换的性质

(1) 序列的傅里叶变换的线性

设

则

2．序列的移位

设

则

3．序列的调制

设

则

4．序列的折叠

设

则

5．序列乘以n 

设

则

6．序列的复共轭

设

则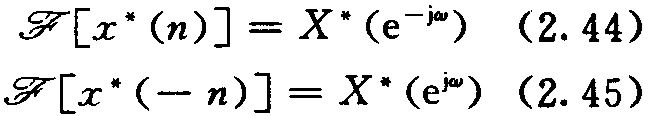

7．序列的卷积

设

则

8．序列相乘

设

则

9.傅氏变换的对称性质

（一）共轭对称序列与共轭反对称序列

1.共轭对称序列：xe(n)=xe*(.n)

设序列：

则

则

根据定义： ，

结论：共轭对称序列的实部是偶对称序列(偶函数)

而虚部是奇对称序列(奇函数)

2.共轭反对称序列：xo(n)=-xo*(.n)

同样有：

结论：共轭反对称序列的实部是奇对称序列(奇函数)

而虚部是偶对称序列(偶函数)

3.任意序列可表示成xe(n)和xo(n)之和:

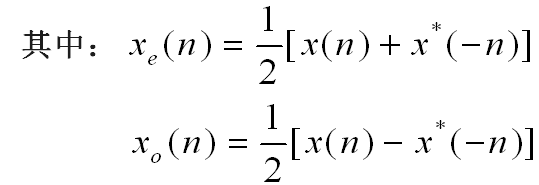
序列的傅里叶变换X(ejω)可以被分解成共轭对称与共轭反对称两部分之和，即

其中：

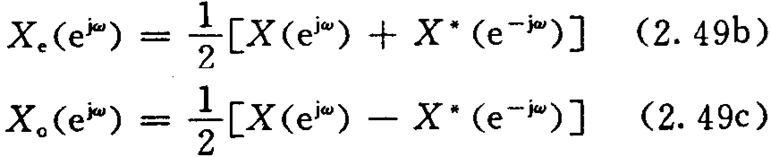
设复序列x(n)的傅里叶变换为X(ejω)，x(n)的实部Re[x(n)]和虚部jIm[x(n)]的傅里叶变换分别为

序列x(n)的共轭对称分量xe(n)和共轭反对称分量xo(n)的傅里叶变换为

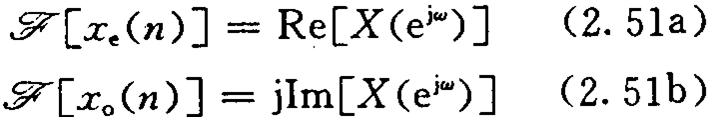
若x(n)为实序列，则这些对称性质将变得特别简单、有用：

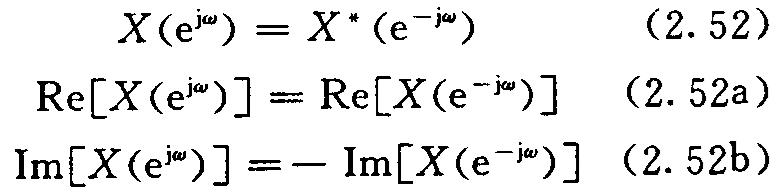
2.4.3离散时间系统的频率响应

一、线性非移变系统的频率响应

系统的频率响应

输入信号为

系统输出

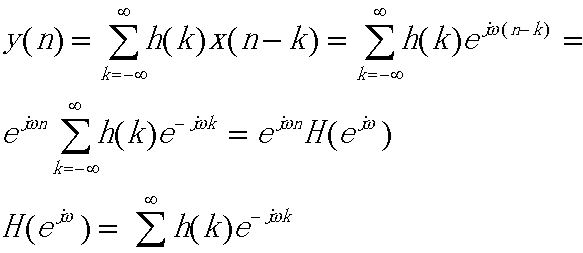
称为单位取样响应为h(n)的系统的频率响应。

二、系统频率响应的特点

(1)H(ejω)是ω的连续函数；

(2) H(ejω)是ω的以2π为周期的函数；

(3) h(n)为实序列时H(ejω)的幅值为偶对称的，相位为奇对称的(在区间)

系统频率响应与单位取样响应的关系：

 H(ejω)是周期性连续函数，可以按傅里叶级数展开

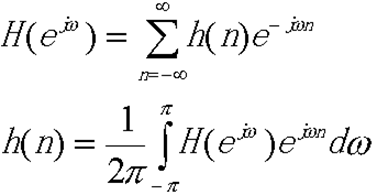
系统的单位取样响应与系统的频率响应互为傅里叶变换对。