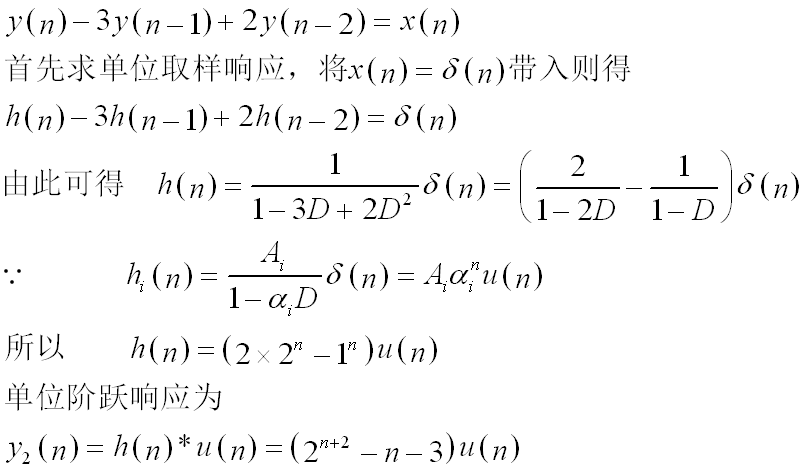2.3.1线性非移变系统
一、系统
¨系统可定义为将输入序列x(n)映射成输出序列y(n)的唯一变换或运算,并用T[]表示,即y(n)=T[x(n)]。
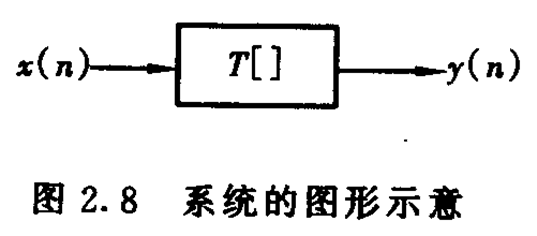
二、线性系统
满足叠加原理的系统称为线性系统。设y1(n)和y2(n)分别是系统对输入x1(n)和x2(n)的响应,即
![]()
若满足
![]()
则此系统是线性系统
三、叠加原理
叠加原理实际上包含两方面性质
1、可加性
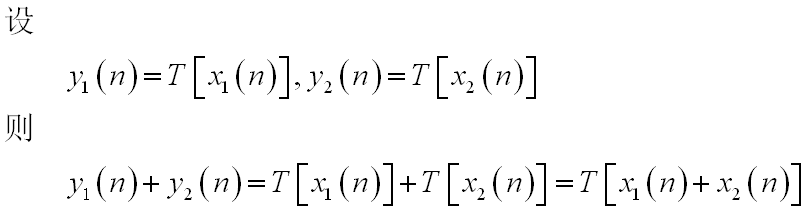
2、比例性(或称为齐次性)
a1y1(n)=a1T[x1(n)]=T[a1x1(n)]
a2y2(n)=a2T[x2(n)]=T[a2x2(n)]
结合上述两点可知,叠加原理的一般表达式为
![]()
四、线性系统的判别
1.通过叠加原理的一般表达式进行判别
(包括可加性和比例性两个方面)
2.根据比例性的特例进行判别:
零输入产生零输出
x(n)=0 时y(n)=0
线性系统判别,例2.1
y(n)=T[x(n)]=5x(n)+3所表示的系统是不是线性系统。
解:
经计算:
T[ax1(n)+bx2(n)]=5[ax1(n)+bx2(n)]+3,
而ay1(n)+by2(n)=5ax1(n)+5bx2(n)+3(a+b)
线性系统判别,例2.2
判断以下系统是否为线性系统: y(n)=4x(n)+6
解:令x1(n)=3, x2(n)=4
则y1(n)+y2(n)=40
T[x1(n)+ x2(n)]=34
不满足可加性不是线性系统
上述两道例题也可以用零输入产生零输出证明
五、非移变系统
若系统的响应与输入信号施加于系统的时刻无关,则称该系统为非移变系统。
即如果输入x(n)产生的输出为y(n),则输入x(n-k)产生的输出为y(n-k)(k为任意整数)。用数学式表示为:若T[x(n)]=y(n),则T[x(n-k)]=y(n-k)。在n表示离散时间的情况下,“非移变”特性就是“非时变”特性。
非移变系统例题
例2.2 证明y(n)=T[x(n)]=nx(n)不是非移变系统
计算T[x(n-k)]=nx(n-k),而y(n-k)=(n-k)x(n-k)。
课后思考题:
1、证明
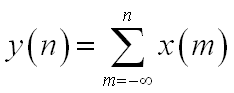
是移不变系统。
2、判定
![]()
是否是移不变系统。
2.3. 2 系统的稳定性和因果性
稳定系统是指对于每个有界输入x(n),都产生有界输出y(n)的系统。即如果|x(n)|≤M(M为正常数),有|y(n)|<+∞,则该系统被称为稳定系统。
一个线性非移变系统稳定的充分和必要条件是其单位取样响应h(n)绝对可和,即
![]()
因果系统是指输出的变化不领先于输入的变化的系统。
一个线性非移变系统为因果系统的充分必要条件是
![]()
例2.5 已知一个线性非移变系统的单位取样响应为
![]()
讨论其因果性和稳定性。
解:
(1)因果性
因为在n<0时,h(n)≠0,故该系统为非因果系统
(2)稳定性
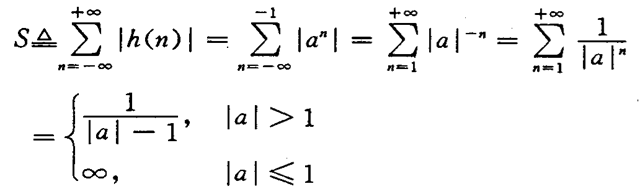
2.3.3 线性常系数差分方程
一、差分方程是由函数序列的差分来表示的。一个函数序列的一阶向后差分表示为:
![]()
二阶向后差分表示为:
![]()
引入单位延迟算子D,即Dy(n)=y(n-1)。
![]()
二阶向后差分可表示为:
![]()
类似地,k阶差分表示为:
![]()
线性常系数差分方程的一般形式为:
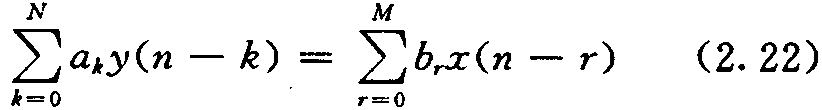
将方程(2. 22)稍加变换后得:
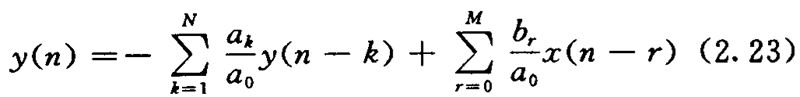
该式说明,系统在某时刻n的输出值y(n)不仅与该时刻的输入x(n)、过去时刻的输入x(n-1),x(n-2)等有关,还与该时刻以前的输出值y(n-1),y(n-2)等有关。
方程(2. 22)的求解可按以下3步进行:
(1)求出对应的齐次方程的通解y1(n);
(2)确定方程(2. 22)的一个特解y2(n);
(3)方程(2. 22)的全解y(n)=y1(n)+y2(n)。
首先求方程(2. 22)的齐次通解。与方程(2. 22)对应的齐
次方程为
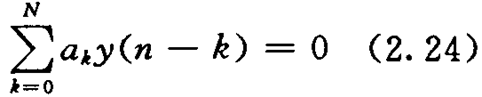
设通解为cαn,利用微分方程的求解方法,得到其特征方程为:
![]()
若特征方程有相异根αi,i=1,2, …,N,则齐次通解
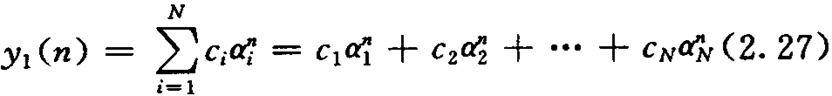
若方程(2. 26)有1个m重根α1,则齐次通解为
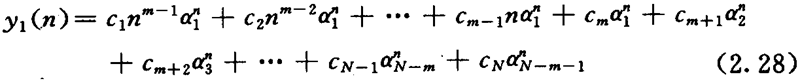
例2. 6 求以下齐次差分方程的通解
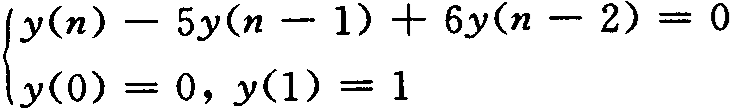
解:特征方程为:
![]()
特征根为:
![]()
于是齐次差分方程的通解为:
![]()
代人初始条件,可求得
![]()
因此通解为
![]()
求方程(2.22)的特解。求特解的方法有比较系数法、递推法和卷积法等。比较系数法与微分方程求特解的方法类似,这里主要介绍卷积法。
卷积法的思路是:由于在零状态下,线性非移变系统对输入x(n)的响应y(n)可用式 (2. 19)表示的线性卷积来计算,所以只要求出系统的单位取样响应h(n),就可求出特解。
根据P21的介绍
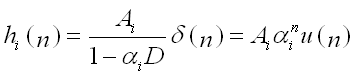
![]()
为特征方程的解。Ai为分解系数。
方程的特解为:
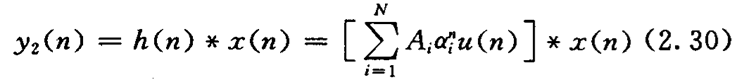
具体,请见例2. 7。
例2.7因果线性非移变系统求单位阶跃响应