15.3.1基本假定和思路
本节课包含二“芝士”点,一个微课视频任务点,一个本节测试任务点(5道单选),一个线下课堂讨论(手工作坊),预计花费时间12分钟。
----------------------我是华丽分割线,请吃个“芝士”---------------------------

1.基本假定
经济由一个部门组成,该部门生产一种既可用于投资也可用于消费的商品;
该经济为不存在国际贸易的封闭经济,且政府部门被忽略;
生产的规模报酬不变;
该经济的技术进步、人口增长及资本这就的速度都由外生因素决定;
生产要素的边际收益递减;
社会储蓄函数为S=sY ,s为储蓄率
----------------------我是华丽分割线,请吃个“芝士”---------------------------

2.思路
先论述没有技术进步的新古典增长模型,再论述具有技术进步的新古典增长模型。
15.3.2模型的构建
本节课包含二个“芝士”点,一个微课视频任务点,一个本节测试任务点(5道单选),一个线下课堂讨论(手工作坊),预计花费时间12分钟。
----------------------我是华丽分割线,请吃个“芝士”---------------------------

1.没有技术进步的新古典增长模型
在没有技术进步的情况下,设生产函数为
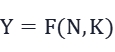
Y为总产出
N和K分别为总量劳动和总量资本
新古典增长模型的基本方程式:
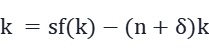
资本深化=人均储蓄(投资)−资本广化
----------------------我是华丽分割线,请吃个“芝士”---------------------------

2.具有技术进步的新古典增长模型
现在构建具有技术进步的新古典增长模型,设经济的生产函数为:

AN称为有效劳动
具有技术进步的新古典增长模型的基本方程:
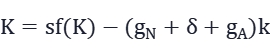
15.3.3稳态及其条件
稳态的定义
意味着包括资本存量和产出在内的有关内生变量将不会随时间的推移而变化的一种状态。如下图中D点所对应的状态即为模型的稳态。
没有技术进步的新古典增长模型,稳态的条件:

具有技术进步的新古典增长模型,稳态的条件:
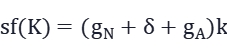

15.3.4稳态时的增长率
根据新古典增长模型,只有技术进步才能解释经济持续增长和生活水平的持续上升。
没有技术进步的新古典增长模型的稳态增长率
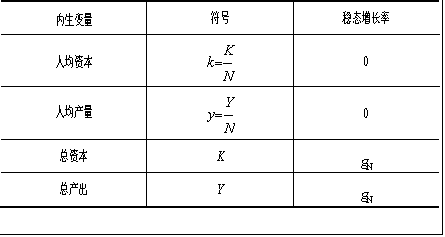
具有技术进步的新古典增长模型的稳态增长率
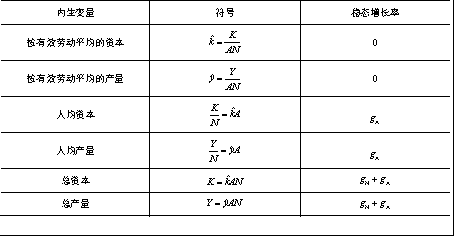
15.3.5模型的应用
本节课包含二个“芝士”点,一个微课视频任务点,一个本节测试任务点(5道单选),一个线下课堂讨论(手工作坊),预计花费时间12分钟。
对收入差异的解释:
短期看,储蓄率的增加提高了稳态的人均资本和人均产量。
长期看,随着资本的积累,增长率逐渐降低,最终又回落到人口增长率的水平。
储蓄率增加对稳态的影响:
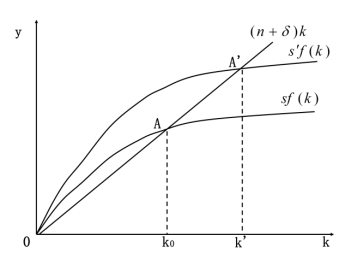
结论一:人口增长率的增加使人均资本的稳态水平降低,进而降低了人均产量的稳态水平。
结论二:人口增长率的上升增加了总产量的稳态增长率。
人口增长的影响:

----------------------我是华丽分割线,请吃个“芝士”---------------------------

对增长率差异的解释
1.新古典增长模型形成了如下三个预言:
l 如果两个国家的储蓄率(或投资率)相同,但初始人均资本(从而初始人均收入)不同,那么,初始人均资本较低的那个国家将具有较高的经济增长;
l 如果两个国家的初始人均资本相同,但是投资率不同,那么,投资率高的那个国家将具有较高的经济增长;
l 如果一个国家提高投资水平,那么,它的收入增长率也将提高。
----------------------我是华丽分割线,请吃个“芝士”---------------------------

2.资本的黄金律水平
Ø 对应于不同的储蓄曲线,就决定了图中不同的稳态人均资本
Ø kgold被称为资本的黄金律水平,因为对应稳态人均消费的最大值cgold

横坐标表示人均资本
纵坐标表示人均产量、人均储蓄和人均消费。
15.3.6重要结论
Ø 生产函数和储蓄率相似的经济体,如果初始人均收入较低,其增长速度会较快,而初始人均收入较高的经济体,其增长速度则较慢。
Ø 储蓄率较高,使得投资水平较高,导致人均资本和人均产出水平较高,但是不影响这些变量的长期增长率。
Ø 较高的人均增长率会降低人均产出水平。
Ø 一旦经济达到稳态,人均产出的增长率就只取决于技术进步的速率。换句话说,只有技术进步才能解释一国或地区经济的持续增长和生活水平的持续提高。


