§2.2球面光学成像系统、

•本节讨论有限大小的物体经过折射球面在近轴区的成像情况

•有限大小的物体经折射球面的成像，除了物象位置外，还会涉及像的正倒、虚实、放大率等问题。

•细小物平面以细小光束成像

 物平面是靠近光轴的很小的垂轴平面，并以细光束成像，就可以认为其像面也是平的，成的是完善像，称为高斯像，我们将这个成完善像的不大区域称为近轴区

一 单个折射球面成像

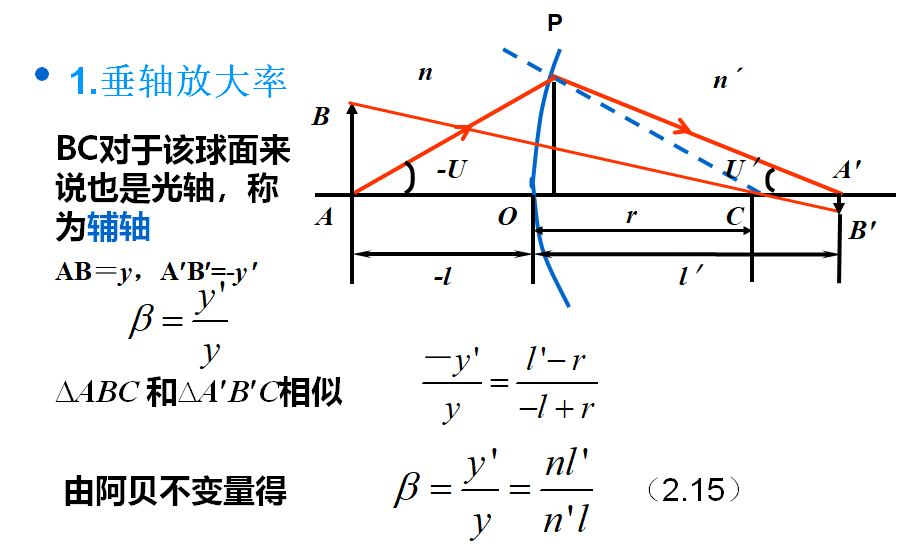
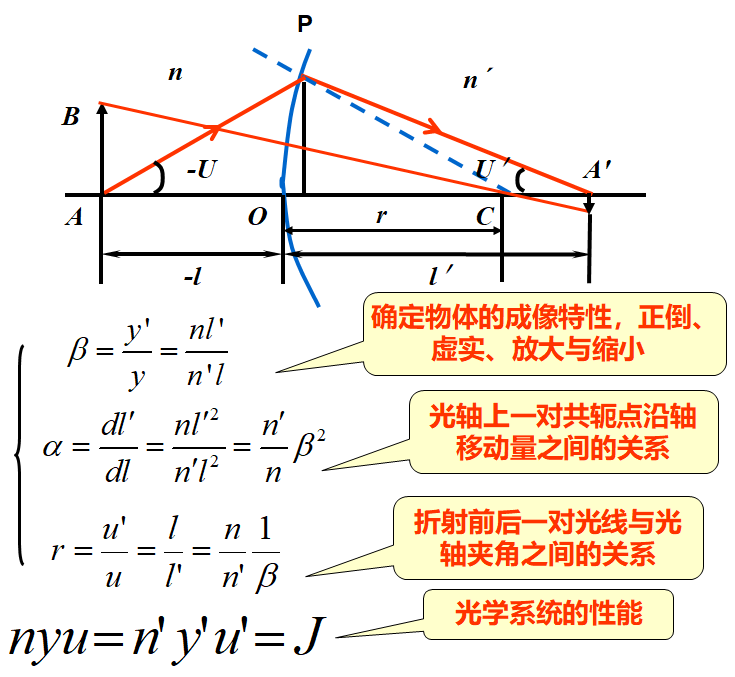
当求得一对共轭点的截距l和l¢后，可求得通过该共轭点的一对共轭面上的垂轴放大率。

 b仅和共轭面位置有关。

在同一对共轭面上，b为常数，所以像和物相似

当|b|> 1，为放大像；当|b|<1，为缩小像

•2.轴向放大率

指光轴上一对共轭点沿轴移动量之间的关系

物点沿轴移动一微小量dl，相应的像移动dl¢

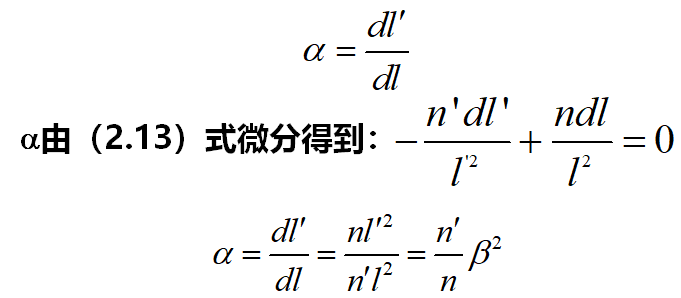
讨论：

①a恒为正，当物点沿轴向移动时，像点沿轴同向移动

②一般，a¹b，即空间物体成像后要变形。如正方体

③只有在dl很小时才适用

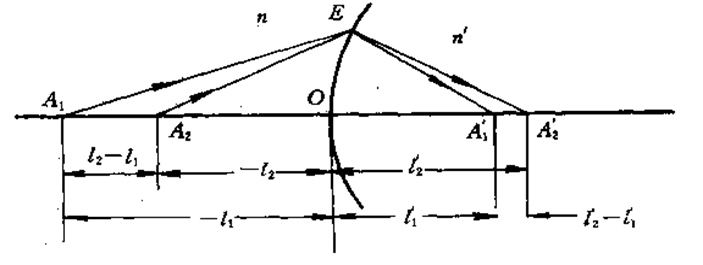
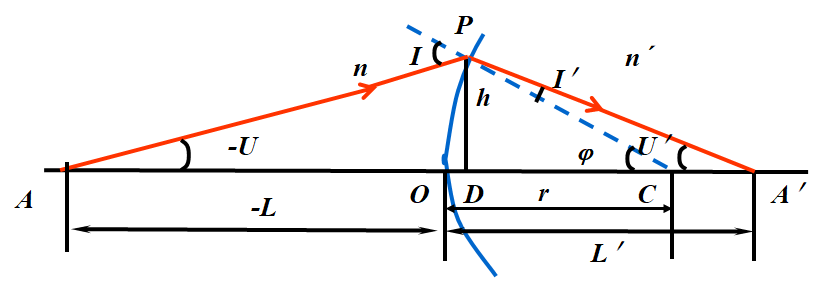
如果物点沿轴移动有限距离，如图所示，此距离显然可以用物点移动的始末两点A1和A2的截距差l2－l1 来表示，相应于像点移动的距离应为l 2¢-l 1¢

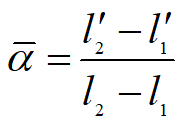
对A1和A2点

        

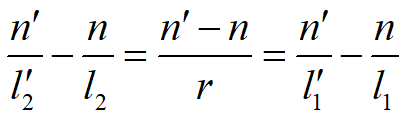
移项整理得

       

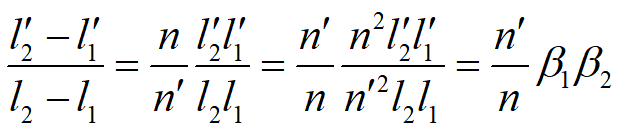
即

       

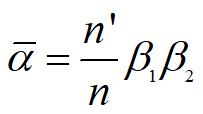
其中b1 和b2 分别为物在A1和A2两点的垂轴放大率

3.角放大率

共轭光线与光轴夹角u¢和u 的比值，称为角放大率

                                       

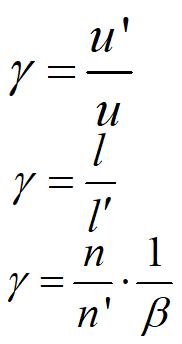
4. 三个放大率之间的关系

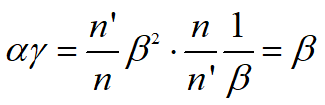
5. 拉亥不变量J

在公式b=y¢/y=nl¢/n¢l 中，利用公式g=l/l¢=u /u¢，

此式称为拉格朗日－亥姆霍兹恒等式，简称拉亥公式。其表示为不变量形式，用J 表示，简称拉亥不变量。

J 表征了这个光学系统的性能，即能以多高的物、多大孔径角的光线入射成像。 J 值大，表明系统能对物体成像的范围大，成像的孔径角大，传输光能多。同时，孔径角还与光学系统分辨微细结构的能力有关。所以J 大的系统具有高的性能。

•1.完善成像的等光程条件

•2.轴上物点单个折射球面的光路计算公式

•3.轴上物点近轴光路

4.细小物平面近轴光成像

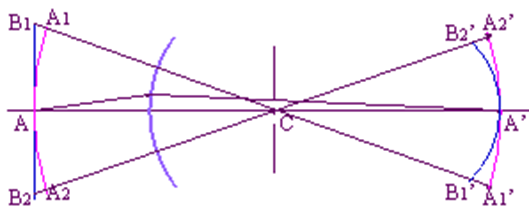
①物平面以细光束经球面所成的像

    细光束，A—— 》 A'，完善成像

    同心球面 A1A A2—— 》曲面A1'A'A2' ，完善成像

    由物象位置公式， l 变小， l'也变小，平面B1AB2—》曲面B1'A'B2'，不再是平面,像面弯曲

② 细小物平面以细光束经折射球面成像：

     对于细小平面，认为像面弯曲可以忽略，平面物 —— 》平面像，完善成像

二、球面反射镜   

在折射面的公式中，只要使n¢ =-n，便可直接得到反射球面的相应公式。

1．球面反射镜的物象位置公式

将n¢=-n 代入（2.13）式，可得

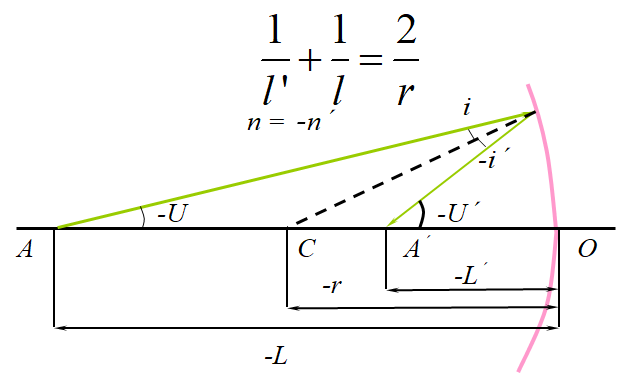
2．球面反射镜的焦距

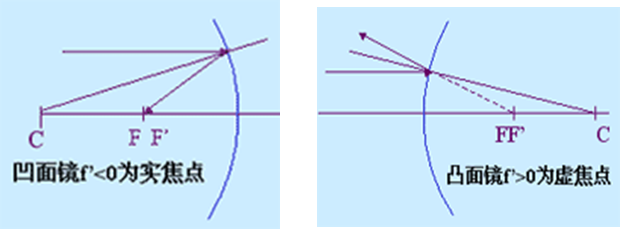
球面反射镜的二焦点重合，

凹球面反射镜: r< 0，f¢< 0，实焦点，光束会聚

凸球面反射镜:  r > 0 , f'>0 ，虚焦点，光束发散

3． 球面反射镜的放大率公式

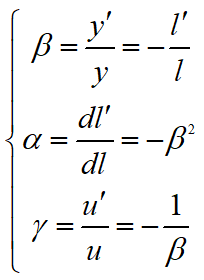
α恒为负值，当物体沿光轴移动时，像总以相反方向沿轴移动。当物体经偶数次反射时，轴向放大率为正。

三共轴球面系统   

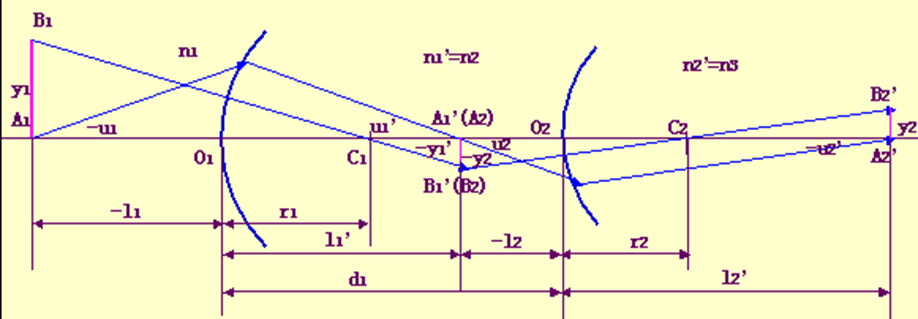
已知

（1）各球面曲率半径r1,r2,……rk

（2）各表面顶点的间隔d1,d2,….. ,dk-1

（3）折射率 n1, n2, ……, nk+1

讨论经共轴球面系统成像的几个光路计算问题。

1.由入射光线求出射光线

•对一个面的操作+ 过渡

•上面讨论的单个折、反射球面的光路计算及成像特性，对构成光学系统的每个球面都适用。

•只要找到相邻两个球面之间的光路关系（过渡公式），就可以解决整个光学系统的光路计算问题，并分析成像特性。

光线在折射面上入射高度h的过渡公式。

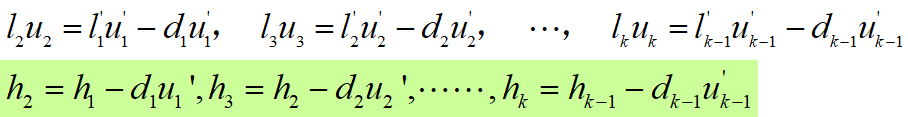
2. 共轴球面系统的拉亥公式

拉亥不变量J不仅对一个折射面的两个空间是不变量，而且对整个光学系统的每一个面的每一个空间都是不变量。

J是光学系统的一个重要特征量。和单个折射球面的相同，J值越大，光学系统就具有更高的功能。

3.成像放大率

•总的放大率为各折射球面放大率的乘积

 例如照相机的变焦镜头通常是由四部分组成：前固定组、变倍组、补偿组和后固定组。变焦镜头的放大率就等于四部分放大率之积。

•三个放大率之间的关系与单个折射球面的完全一致