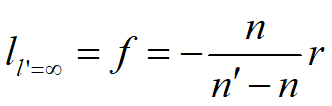§2.1  近轴光学系统的光路计算

•大多数光学系统都是由折、反射球面或平面组成的共轴球面光学系统

•折射球面系统具有普遍意义

•光学系统的成像实际上是物体各点发出的光线经光学系统逐面折、反射的结果

•所以首先讨论单个折射球面折射的光路计算问题，再过渡到整个光学系统

•实际光学系统中，光线和球面的位置可能是多种多样的，为使推导出的公式在各种情况下都适用，对参数符号做了规定

一 基本概念和符号规则

1.基本概念

•光轴：若光学系统由球面组成，它们的球心位于同一直线上，则称为共轴球面系统，这条直线为该光学系统的光轴。实际上，光学系统的光轴是系统的对称轴

•子午面：通过物点和光轴的截面

•物方截距：L＝OA，像方截距：L′=OA′

•物方孔径角:U，像方孔径角：U′

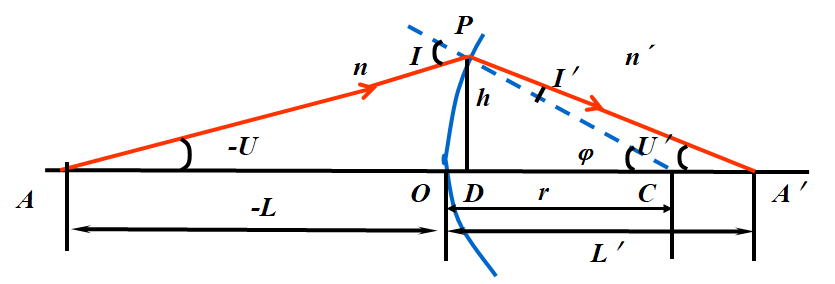
2. 符号规则：

Ø光线的传播方向：自左向右为正

Ø线段

u沿轴:以O为原点， －L，r，L′

u垂轴 h

u球面的曲率半径：球心在球面顶点的右方为正，反之为负

Ø角度

u光线与光轴的夹角：光轴转向光线 -U，U′

u光线与法线的夹角：光线转向法线 I，I′

u光轴与法线的夹角：光轴转向法线 j 

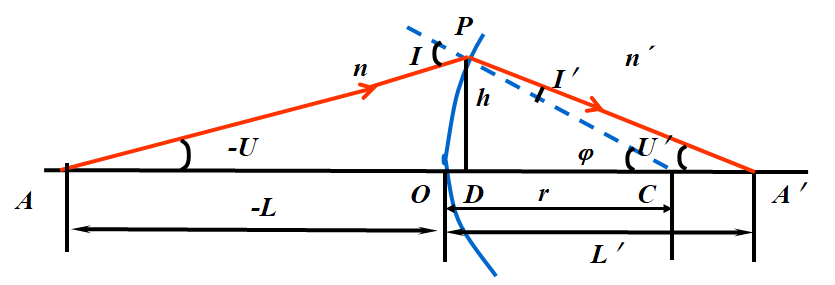
二 单个折射球面的光路计算

•在给定单个折射球面的结构参量n、n¢和r 时，由已知入射光线坐标 L 和U，计算折射后出射光线的坐标L¢和U ¢

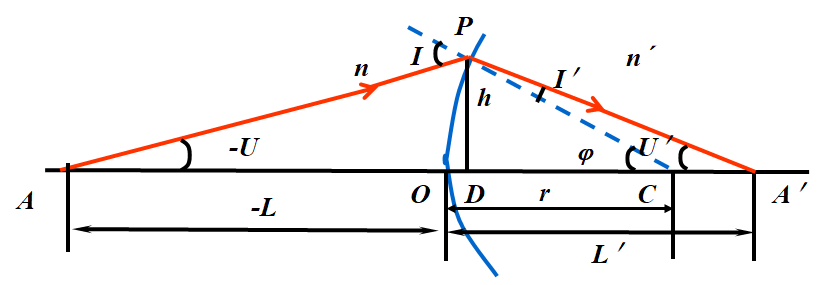
   在ΔAPC中，

   应用正弦定理有 

   或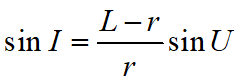

   在P点，由折射定律得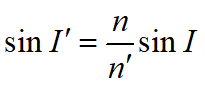

   由图可知

   所以

   同样，在三角形A'PC中应用正弦定理有

                         

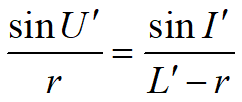
   化简后得像方截距

    式(2.1-2.4)就是计算子午面内光线光路的基本公式。给出一组L、U，可计算L′、U′

由公式可知，L′是U的函数。不同 U的光线经折射后不能相交于一点，点－》斑　

　　　　　

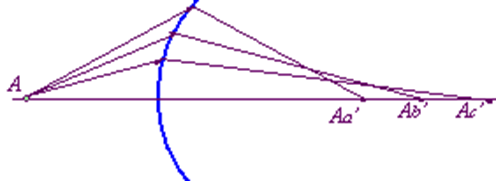
单个折射球面对轴上物点成像是不完善的，这种成像缺陷称为像差，是以后将会讨论到的球差。

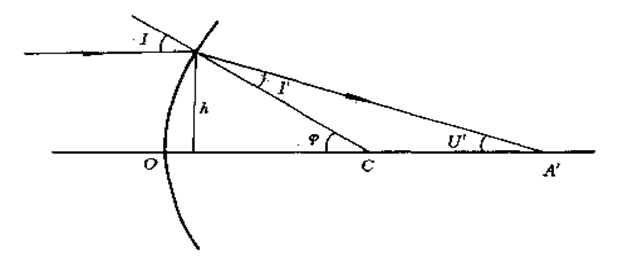
三单个折射球面近轴光线的光路计算

•1.近轴光：如果限制U角在一个很小的范围内，即从A点发出的光线都离光轴很近，这样的光线称为近轴光

光轴附近的一个小区域称为近轴区。           

研究近轴区的物象关系的光学称为近轴光学。

在近轴几何光学中，经常用到以下近似公式（一级泰勒展开）

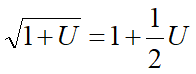
U为物方孔径角，是个很小值（<<1rad）,当U<5°，近似代替误差大约为1%. 近似的有效范围根据精度要求可扩展至10-30°

2.近轴光路计算公式  （2.6- 2.9）P27

在近轴条件下：OD << r

    校对公式

利用大L 和小l计算公式及其它有关的公式计算光线光路的过程通常称为光线追迹。在近轴光的光路计算中U角可以任取

3.近轴光线经折射球面计算的其他形式

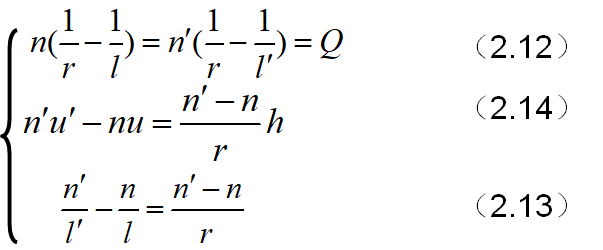
一个公式的三种不同表示形式，便于不同场合的应用

上式称为阿贝（Abbe）不变量。给定共轭点，

Q物＝Q像，Q的大小与物像共轭点的位置有关。

（2.13）式表示物像位置的关系。   

（2.14）式表示u和u¢的关系

4.（近轴区）折射球面的光焦度，焦点和焦距

上式右端仅与介质的折射率及球面曲率半径有关，对于一定的介质及一定形状的表面来说是一个不变量。若n'、n、r 一定，则l变化 l’变化，它是表征折射面偏折光线的能力，称为折射球面的光焦度：

若物点位于左方无限远处的光轴上，此时入射光线平行于光轴，经球面折射后交光轴的交点记为F¢。这个特殊点是轴上无限远物点的像点，称为折射球面的像方焦点。此时的像距称为像方焦距，用f¢表示。

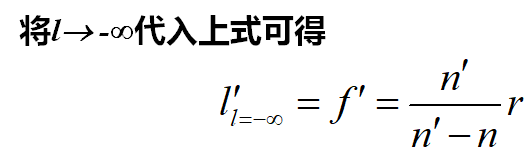
像距为无限远时所对应的物点，称为折射球面的物方焦点或前焦点，记为F，此时的物距称为物方焦距或前焦距，记为f，有