第一节 几何光学的基本定律

• 几何光学是以光线的概念为基础，采用几何的方法研究光在介质中的传播规律和光学系统的成像特性

• 按几何光学的观点，光经过介质的传播问题可归结为四个基本定律：光的直线传播定律、光的独立传播定律、光的反射定律和折射定律

ref: 几何光学的发展

• 先秦时代  《墨经》 

• 330-260BC  欧几里德《反射光学》

• 965-1038AD  阿勒·哈增《 光学全书》

• 十七世纪  开普勒、斯涅尔、笛卡儿、费马

折射定律的确立，使几何光学理论得到很快的发展。

1.光波、光线、光束
light waves、raysand beams

•光波

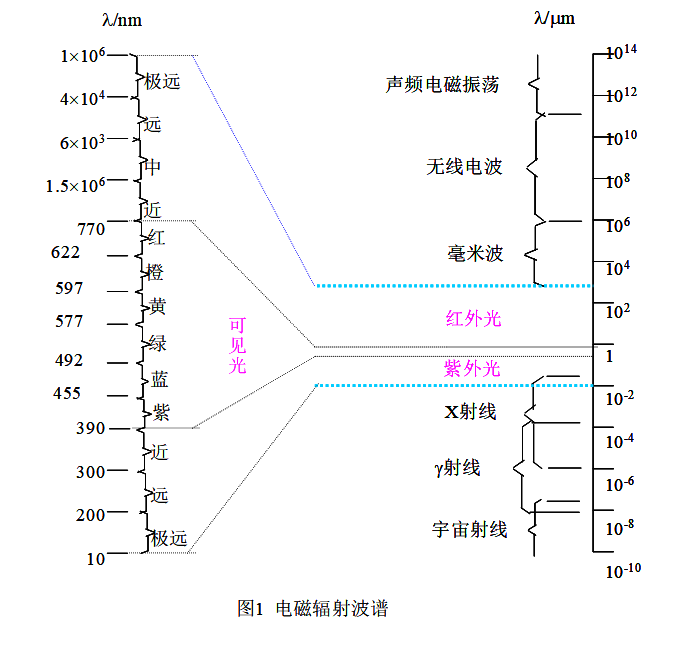
 光波是一种电磁波，是一定频率范围内的电磁波，波长比一般的无线电波的短

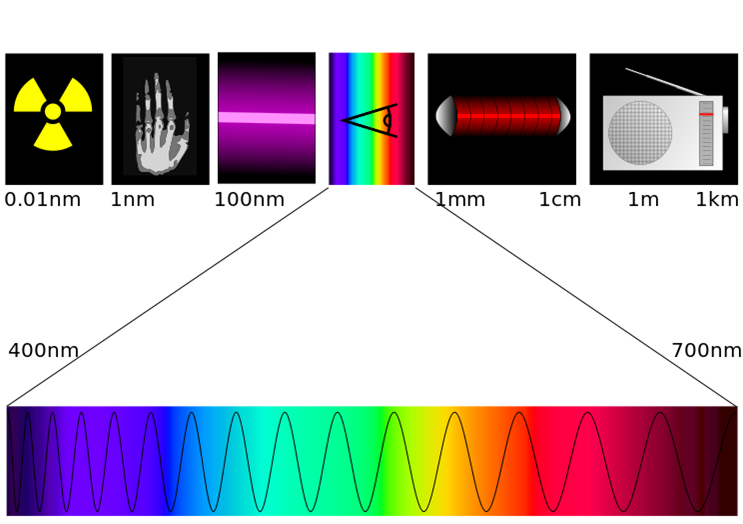
•可见光：400nm-760nm

•紫外光：5-400nm

•红外光：780nm-40µm

•近红外：780nm-3µm

•中红外：3µm－6µm

•远红外：6µm－40µm

•光源light sources

Ø光源：任何能辐射光能的的物体

Ø点光源：无任何尺寸，在空间只有几何位置的光源

  实际中是当光源的大小与其辐射光能的作用距离相比可  忽略不计，则视为点光源

•光学介质optical mediums

Ø光学介质：光从一个地方传至另一个地方的空间。空气、水、玻璃

Ø各向同性介质:光学介质的光学性质不随方向而改变

Ø各向异性介质：单晶体（双折射现象）

Ø均匀介质：光学介质的不同部分具有相同的光学性质

 均匀各向同性介质

•波前 wave front

Ø波前：某一瞬间波动所到达的位置构成的曲面

Ø波面：传播过程中振动相位相同的各点所连结成的曲面

 在任何的时刻都只能有一个确定的波前；波面的数目则是任意多的

Ø球面波：波面为球面的波，点光源

Ø平面波：无穷远光源

Ø柱面波：线光源

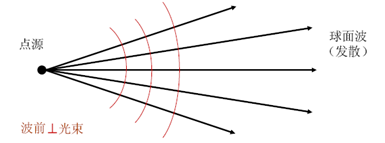
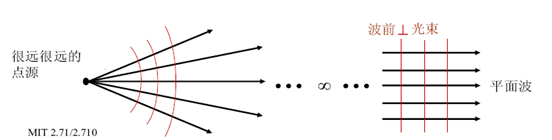
•光线：传输光能的有方向的几何线

Ø在各向同性介质中，光沿着波面的法线方向传输，所以波面的法线就是光线

•光束

Ø光束：具有一定关系的光线的集合

Ø同心光束：同一个发光点发出或相交于同一点

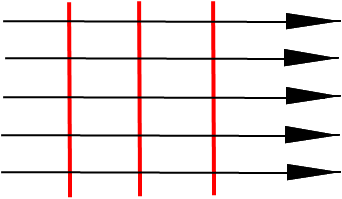
Ø平行光束：发光点位于无穷远，平面光波

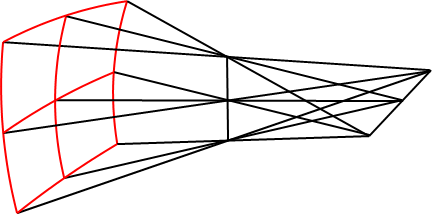
Ø像散光束：既不相交于一点，又不平行，但有一定关系的光线的集合，与非球面的高次曲面光波相对应

同心光束

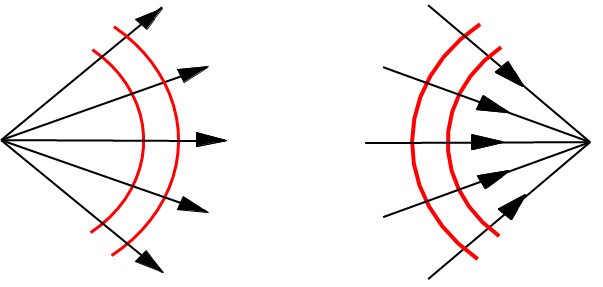
平行光束

ref: 像散光束

•光线既不平行，又不相交，波面为曲面。

ref: 工程思路

•在几何光学中研究成像时，主要要搞清光线在光学元件中的传播途径，这个途径称为光路。

•实际做法：从光束中取出一个适当的截面，再求出其上几条光线的光路，即可解决成像问题。这种截面称为光束截面。

2.几何光学的适用条件

•光学系统的尺度远大于光波的波长

•介质是均匀和各向同性的

3.基本定律

•光的直线传播定律（P4）

Ø各向同性的均匀介质

Ø局限性

•当光经过尺寸与光波长接近或更小的小孔或狭缝时，将偏离直线，“光的衍射”

•当光在非均匀介质中传播时，沿曲线传播

•独立传播定律（P4）

Ø从不同光源发出的光线，在空间某点相遇时，彼此互不影响，各光线独立传播

Ø利用这条定律，研究某一光线传播时，可不考虑其它光线的影响。大大简化我们对光线传播的研究

•光的反射和折射定律（P5）

 光传播到两种不同介质的光滑分界面上时，继续传播的光线或返回原介质，或进入另一介质。前者称为光的反射，后者为光的折射。

•光的反射定律Ø同一平面内；法线的两侧，且I′′=-I•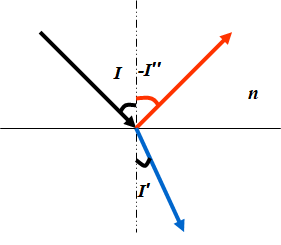

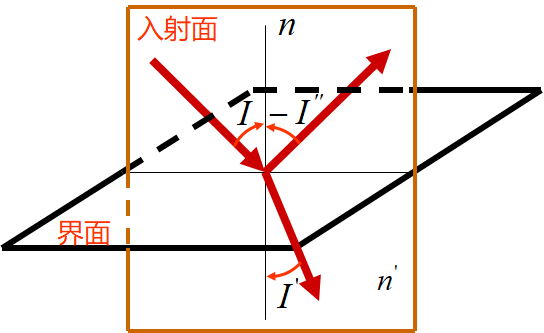
•折射定律（P5下）

Ø在同一平面内

Øn×sinI=n′×sinI′（与入射角无关）

•折射率n：表征透明介质光学性质的重要参数之一。

Øn=c/v,描述介质中的光速相对于真空中的光速减慢程度的物理量Ø空气，n 略大于1（实际应用中大都假设为≈1）

Ø水，n ≈1.3

Ø玻璃，n ≈1.45 –1.75

Ø光折射晶体，如铌酸锂n≈2.2 –2.3

思考题

•反射定律可以看作折射定律的特殊情况(n′=-n)？！

•nab

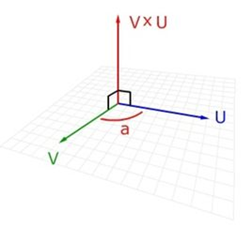
补充：单位向量书写法

•P6•单位向量：Q，入射光线的方向。

•法线单位向量: N

•折射定律：n Q×N= n'Q' ×N

•反射定律：Q×N= －Q' ×N

4. 马吕斯定律(P7)

•马吕斯定律指出，光线束在各向同性的均匀介质中传播时，始终保持着与波面的正交性，并且入射波面与出射波面对应点之间的光程均为定值。(1808年)

•偏振，找波面。

•光程：光在介质中经过的几何路径l和该介质的折射率n的乘积

•L＝n×l=c/v×l=c×l/v=c×t（t为光在介质中传播的时间）

Ø光在某种介质中的光程，等于相同时间内光在真空中的传播距离。

Ø只要光经过不同介质中的传播时间相同，则光程也相同

Ø在任意两个波面之间的所有光线，光程也相同，（波面是相同时间到达点的曲面）

Ø光经过若干种介质时，光程为各介质折射率与几何路径乘积之和。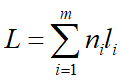

Ø若介质为非均匀，折射率连续变化，则

5. 费马原理(P8)

•几何光学的三个基本定律，说明了光从一点传播到另一点的传播规律，而费马原理则从光程的角度阐述光的传播规律

•费马原理，不是建立在实验基础上的定律，也不是从数学上导出的定理，而是一个最基本的假设。

•费马原理是几何光学中光传播的理论基础。很多定律和对事物总图像的描述，均可由其得到正确的结果，但不是一种计算工具。

•费马原理：光是沿着光程为极值（极大、极小或常量）的路径传播的。（1679年）

•可推导光基本定律

•费马原理规定了光线传播的唯一可实现的路径，不论光线正向传播还是逆向传播，必沿同一路径。因而借助于费马原理可说明光的可逆性原理的正确性

•对于光程取极大或常量的情况

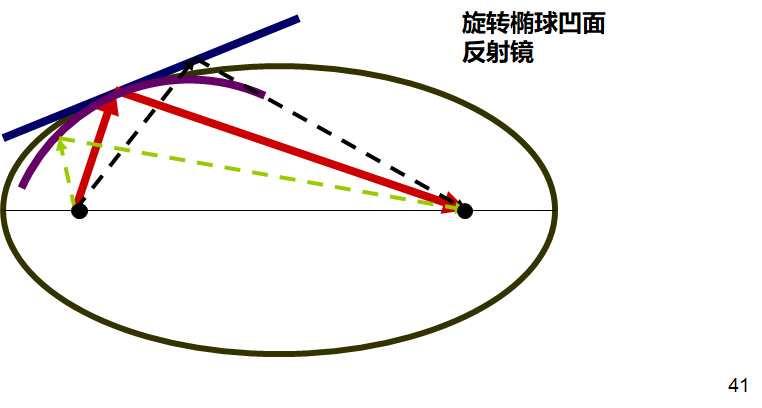
马吕斯定律 Malus law

 垂直于波面的光线束，经过任意多次反射和折射后，出射波面仍和出射光束垂直，且入射波面和出射波面对应点之间的光程相等。

  费马原理   在任意两个波面之间的所有光线，光程也相同，（波面是相同时间到达点的曲面）

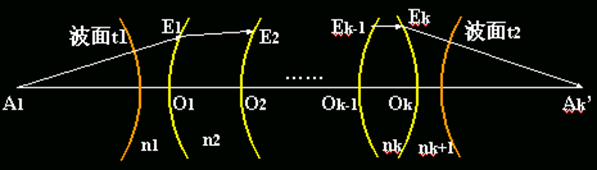
一球面波在某时刻t1形成一波面，该波面经光学系统仍为一球面波，它在某一时刻 t2形成一波面。波面之间的光程总是相等，得等光程条件。

∴③物点及像点之间任意两条光路的光程相等

6.两个重要的光学现象(P11)

•光路可逆

•光的全反射 totalreflection

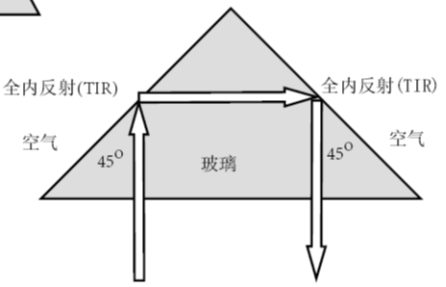
 在一般情况下，光线至透明介质的分界面时，将同时发生反射和折射。在一定的条件下，界面可将入射光线全部反射回去，而无折射现象，这就是光的全反射。

当入射角增大到某一程度时，折射角达到90°折射光线沿界面掠射出去，这时的入射角为临界入射角

当I> Im时，I′变为虚数

折射光消失，能量全部被反射

发生全反射的条件：

光线由光密向光疏介质入射；

入射角>临界角

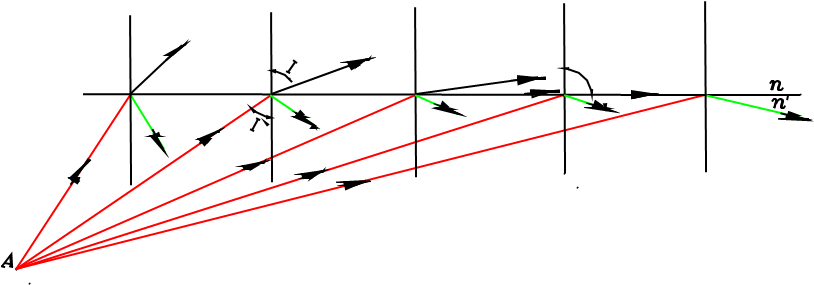
•例如 从玻璃到空气的交界面：n=1.5,n′=1,

    Im=sin-1 1.5/1=41.8°

    I>Im,可发生全反射

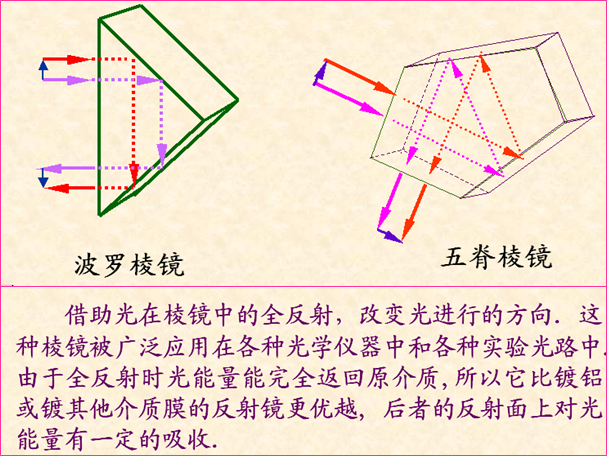
•全反射广泛应用到光学仪器中：

Ø全反射在理论上优于一切镜面反射，在实际的光学仪器中，常利用全反射棱镜代替平面反射镜，以较少光能的反射损失

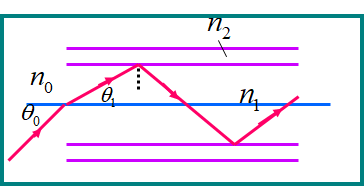
Ø光纤指纹检测

光纤

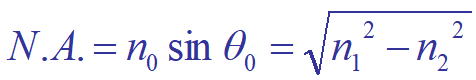
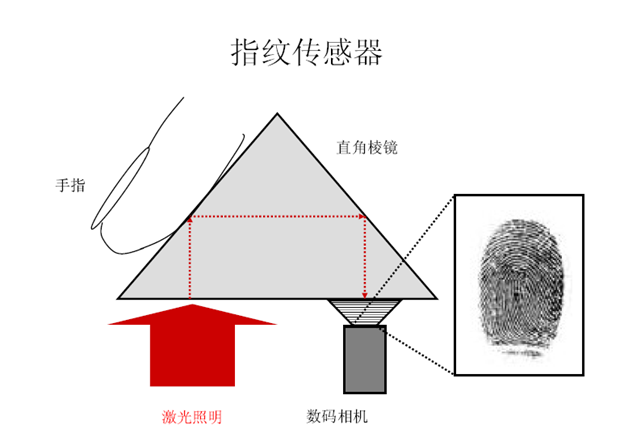
指纹开门/考勤

光线经玻璃射到指纹谷的地方后在玻璃与空气的界面发生全反射，光线被反射到CCD，而射向脊的光线不发生全反射，而是被脊与玻璃的接触面吸收或者漫反射到别的地方，这样就在CCD上形成了指纹的图象

作业：

           1.推导光纤的最大入射角

           2.费马原理证明反射定律

           3.思考题：证明五角棱镜的出射光始终与入射光垂直。