一、离散趋势指标的概念与作用

1.概念：离散趋势指标是反映总体各单位标志值差异（离散）程度的指标。又称标志变动指标、离散程度指标等。

平均指标与离散趋势指标的区别：

平均指标考虑的是如何消除离差，显示集中趋势。而离散趋势指标考虑的是如何计算离差，反映离散的程度及离差的大小。

2.作用

（1）衡量平均数代表性的大小。

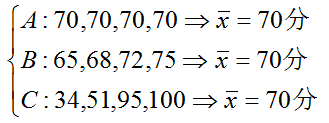
（2）反映变量值分布的离中趋势和离散程度。

（3）反映社会经济现象的均衡性和稳定性。

二、离散趋势指标的种类

（一）全距（极差）

特点：1.优点：意义明确，简单方便。

      2.缺点：比较粗略，未考虑中间变量值的离散情况。

（二）平均差(A.D)

1.概念：平均差是总体各单位标志值与其算术平均数离差绝对值的算术平均数。

2.计算：

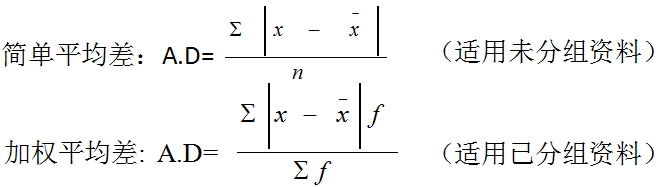
3.特点

    （1）充分考虑了每一数值的离中情况，在反映离中趋势方面比较灵敏，计算方法亦比较简单。

    （2）绝对值运算给数学处理带来很多不便。

（三）方差与标准差

1.概念：方差( )：总体各单位标志值与其算术平均数离差平方的算术平均数；                                 标准差( σ)：总体各单位标志值与其算术平均数离差平方的算术平均数的平方根。

2.基本计算：

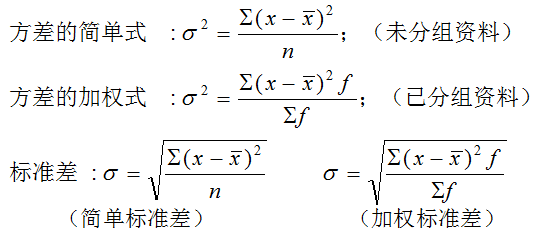
3.是非标志标准差的计算：

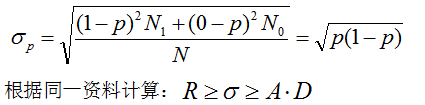
4.判定原则和特点：

 特点：充分考虑了每一数值的离中情况，且避免了取绝对值不方便数学处理的缺点，故运用广泛。

5.方差的数学性质：

总体各单位标志值与其算术平均数的方差最小。

（四）离散系数（相对离中趋势）

1.前述离散趋势指标的特点：

A.均带有与原资料相同的计量单位，属绝对数和平均数离散指标；

B.只有当两总体性质相同、平均数相同时才可用来比较平均数的代表性。

  不同性质的绝对量不可直接对比

    例：       体重        举重         相对水平

   某人      120斤        50斤        50/120=42%

   某只蚂蚁    1克         6克          6/1=600%

2.离散系数的特点：

   A.可用于两个总体平均水平不同时；

   B.可用于两个总体性质不同或计量单位不同时。