（一）三者间的关系

1.数量关系

（1）对称分布：此处三者均等于35。

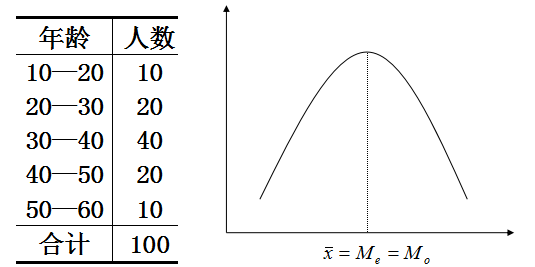
（2）偏态分布

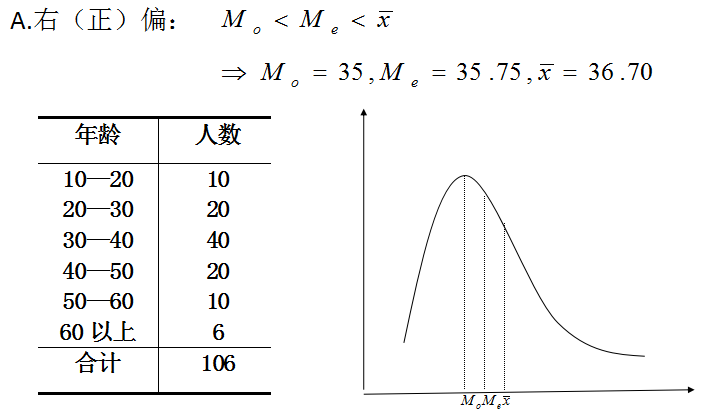
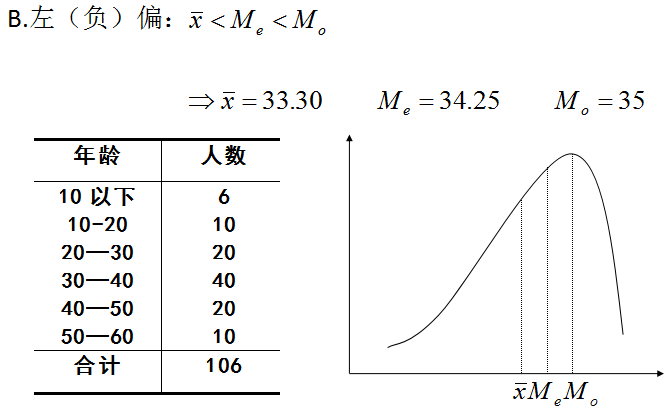
2.卡尔•皮尔逊经验公式：

适度偏斜情况下，众数与中位数之间的距离，大约为中位数到算术平均数之间距离的两倍。

（二）众数、中位数和均值的应用场合

众数一般用来描述分类变量（定性数据），特别是那些有许多个值的分类变量，例如学历、对事物的态度等。例如，在某一地区学历的众数是硕士生，对事物的态度的众数是中立。

当一组数据的直方图显示出非对称或非正态分布时，常常使用中位数是，例如房价和收入数据。

由于均值容易受到极大值或极小值的影响，因此，当数据集有极端值时，最好不使用均值。如果数据的分布是不对称的，最好使用中位数（或众数）而不是均值，因为中位数对极端值不敏感。

总之，如果分布的偏斜程度很高，均值将不能作为一个很好的度量。相对而言，中位数和众数的代表性更强。

  1.注意观察总体的同质性；

  2.应用组平均数补充说明总体平均数；

  3.注意极端值的影响。