（一）中位数

1.定义：

将变量值按大小次序排列，处于中间位置的变量值即为中位数 => Me

[例]某科室由9人组成，其年龄分别为：24,25,25,26,26,27,28,29,55

2.计算

（1）当资料未分组时，中点位置=（n+1）/2；

     当n为奇数时， Me =中间位置的那个变量值；

     当n为偶数时，如24,25,25,26,26,27,28,29

      Me =中间位置两侧的两个变量值的简单平均。

（2）当资料已分组且形成单项式变量数列时，中点位置=∑f/2

（3）资料已分组且形成组距式变量数列

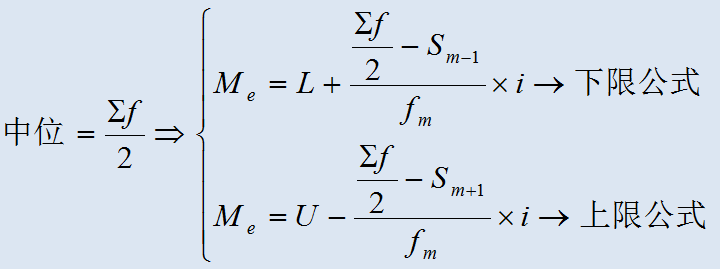
    （A）L为中位数所在组的下限，U为上限；

    （B）i为中位数所在组的组距；

    （C）Sm-1 为小于中位数的各组次数之和；

    （D）Sm+1为大于中位数的各组次数之和；

    （E）fm为中位数所在组的次数。

3.注意的问题

（1）不受极端值的影响，比较稳健。

（2）中位数的取值只与中间位置的一或两个数值有关，利用信息不充分，忽略了其它数据的大小，并且不适合于代数运算。 

(二)众数

1.定义：

出现次数最多的变量值。用Mo表示。

A. 20,15,18,20,20,22,20,23；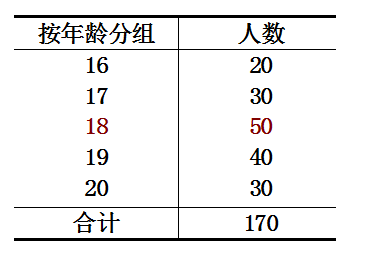 

        n=8     Mo=20

B.20,20,15,19,19,20,19,25；      

  n=8    Mo=20      Mo=19

C. 10,11,13,16,15,25,8,12；

     n=8，但没有众数

2.计算

（1）当资料为单项式数列时。先确定众数组;再确定众数：Mo=18

（2）当资料为组距式数列时。先确定众数组；再用下述公式计算：

符号含义：

（A）L为众数组的下限，U为上限；

（B）i为众数组的组距；

（C）1=fm－fm-1，即众数组的次数与前一组次数之差；

   2=fm －fm+1，即众数组的次数与后一组次数之差。

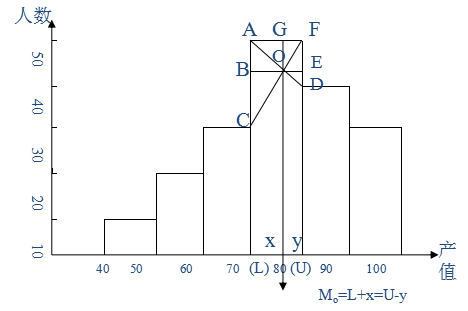
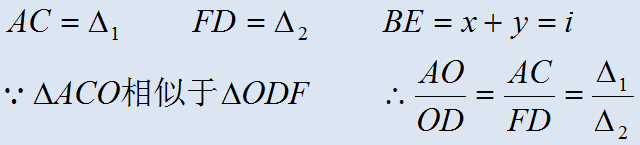
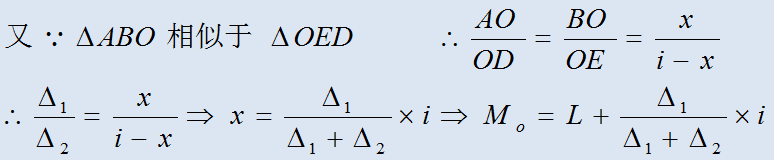
3.注意问题

（1）优点：不受极端值的影响。

（2）缺点：未利用所有信息，缺乏敏感性和不适合代数运算。