奠基性的计算思维有哪些？

0和1是实现任何计算的基础；社会/自然与计算融合的基本手段；0和1是连接硬件与软件的纽带；0/1是最基本的抽象与自动化机制。 

程序是基本动作(指令)的各种组合，是控制计算系统的基本手段。

递归是最典型的构造程序的手段；递归函数是可计算函数的精确的数学描述；递归函数是研究计算学科理论问题的基础。

人类应具备的第三种思维——计算思维

计算思维是运用计算机科学的基础概念进行问题求解、系统设计、以及人类行为理解等涵盖计算机科学之广度的一系列思维活动，由周以真于2006年3月首次提出。2010年，周以真教授又指出计算思维是与形式化问题及其解决方案相关的思维过程，其解决问题的表示形式应该能有效地被信息处理代理执行。

计算思维关注的是人类思维中有关可行性、可构造性和可评价性的部分，当前环境下，理论与实验手段在面临大规模数据的情况下，不可避免地要用计算手段来辅助进行。

实验→观察→发现、推断与总结——观察与归纳

假设/预设→定义/性质/定理→证明——推理和演绎

设计、构造与计算——设计与构造

算法的历史

“算法”即演算法的大陆中文名称出自《周髀算经》；而英文名称Algorithm来自于9世纪波斯数学家al-Khwarizmi，因为al-Khwarizmi在数学上提出了算法这个概念。“算法”原为"algorism"，意思是阿拉伯数字的运算法则，在18世纪演变为"algorithm"。欧几里得算法被人们认为是史上第一个算法。第一次编写程序是Ada Byron于1842年为巴贝奇分析机编写求解伯努利方程的程序，因此Ada Byron被大多数人认为是世界上第一位程序员。因为查尔斯·巴贝奇(Charles Babbage)未能完成他的巴贝奇分析机，这个算法未能在巴贝奇分析机上执行。因为"well-defined procedure"缺少数学上精确的定义，19世纪和20世纪早期的数学家、逻辑学家在定义算法上出现了困难。

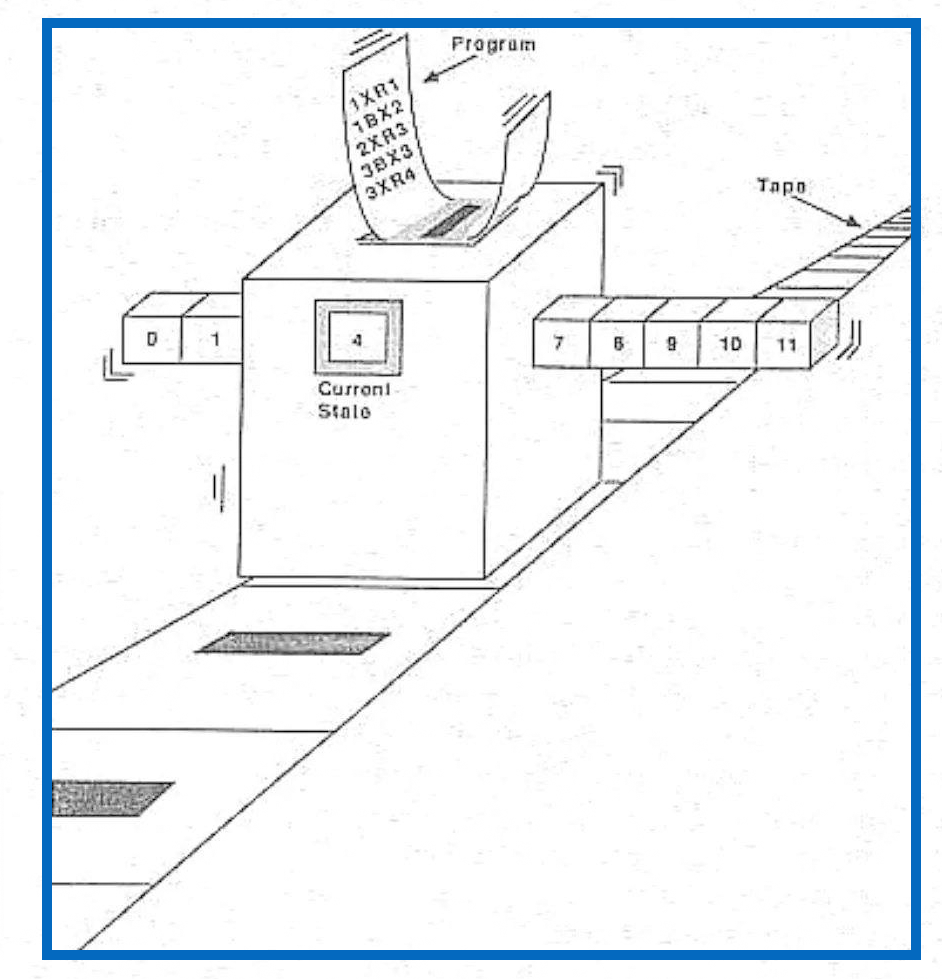
20世纪的英国数学家图灵提出了著名的图灵论题，并提出一种假想的计算机的抽象模型，这个模型被称为图灵机。图灵机的出现解决了算法定义的难题，图灵的思想对算法的发展起到了重要作用。

计算思维的学习方法

• “知识/术语”随着“思维”的学习而展开，“思维”随着“知识”的贯通而形成，“能力”随着“思维”的理解而提高。

• 从问题分析着手，强化如何进行抽象，如何将现实问题抽象为一个数学问题或者一个形式化问题，提高问题表述及问题求解的严谨性。

• 通过图示化方法来展现复杂的思维可以一目了然；通过规模较小的问题求解示例来理解复杂问题的求解方法；通过从社会/自然等人们身边的问题理解到计算科学家是如何进行问题求解。

• 追求“问题”及问题的讨论，通过逐步地提出问题，使自己从一个较浅的理解层次逐步过渡到较深入的理解层次，通过不同视角和递阶的讨论，使自己理解和确定前行的方向。

• 宽度与深度相结合，从宽度学习开始，深度学习结束，既能够使自己理解相关的思维与知识，还能够有助于建立起较为科学的研究习惯与研究方法。

• 思维蕴含在案例中，案例蕴含着思维。