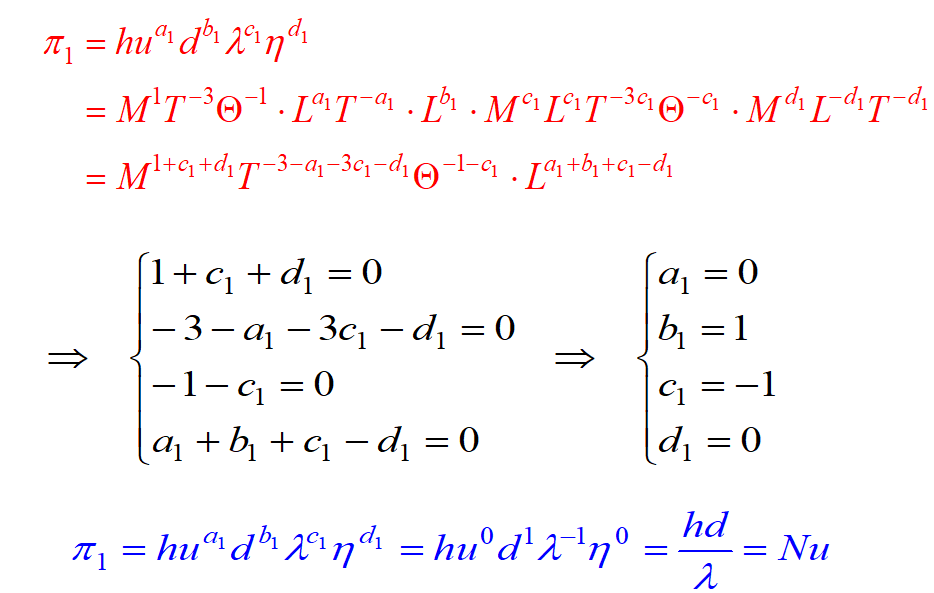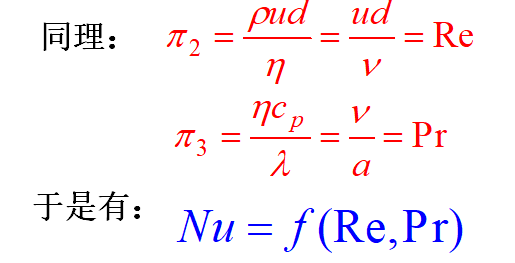通过实验求取对流传热的实用关联式，仍然是传热研究中的一个重要而可靠的手段。然而，对于存在着许多影响因素的复杂物理现象，要找出众多变量间的函数关系，比如

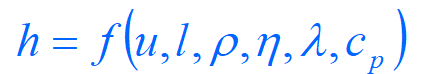
实验的次数十分庞大。为了大大减少实验次数，而且又可得出具有一定通用性的结果，必须在相似原理的指导下进行实验。 

学习相似原理时，应充分理解下面3个问题：①实验时应该测量那些量

②实验后如何整理实验数据

③所得结果可以推广应用的条件是什么

一、物理现象相似的定义

　对于两个同类的物理现象，如果在相应的时刻及相应的地点上与现象有关的物理量一一对应成比例，则称此两现象彼此相似。

①用相同形式且具有相同内容的微分方程式所描述的现象为同类现象，只有同类现象才能谈相似。

②与现象有关的物理量要一一对应成比例。

③对非稳态问题，要求在相应的时刻各物理量的空间分布相似。

凡是相似的物理现象，其物理量的场一定可以用一个统一的无量纲的场来表示。

二、相似原理的基本内容

1、同名特征数相等

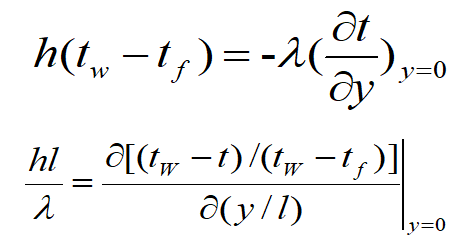
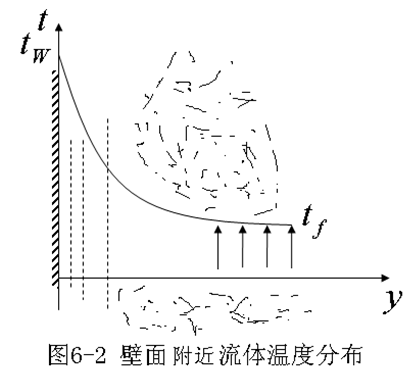
对于两个相似的物理现象，其无量纲的同名物理量的场是相同的，即等式右端的无量纲温度场的梯度应相等，因而有

２、同一类现象中相似特征数的数量及其间的关系

相似原理与量纲分析理论中有一条π定理表述了无量纲特征数之间的相互影响、相互制约的关系。

 定理，即一个表示n个物理量间关系的量纲一致的方程式，一定可以转换为包含 n - r 个独立的无量纲物理量群间的关系。r 指基本量纲的数目。

国际单位制中的7个基本量：

长度[m]，质量[kg]，时间[s]，电流[A]，温度[K]，物质的量[mol]，发光强度[cd]

对于彼此相似的物理现象，无量纲数群间的关系应相同，即所有相似的同类物理现象的特征数方程相同。

３、两个同类物理现象相似的充要条件

①同名的已定特征数－由所研究问题的已知量组成的特征数相等

②单值性条件相似：几何条件、物理条件、初始条件、边界条件

③两种现象相似是实验关联式可以推广应用的条件

三、导出相似特征数的两种方法

１、相似分析法

描写物理现象的微分方程组及定解条件给出了各个物理量之间相互影响与制约的基本关系。

以一维非稳态导热问题为例说明各无量纲数间的相互关系。

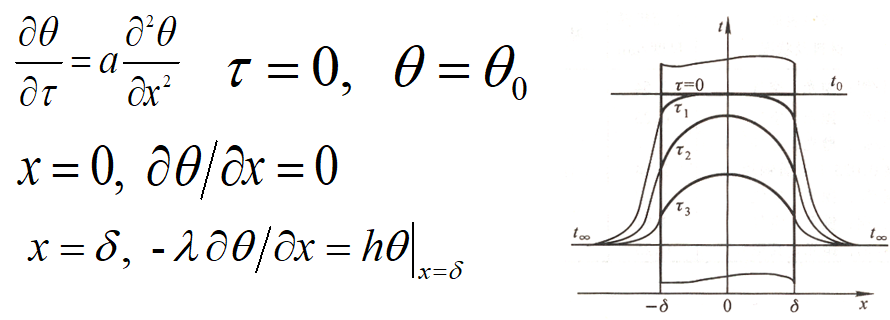
在已知物理现象数学描述的基础上，建立两现象之间的一系列比例系数(相似倍数)，并导出这些相似系数之间的关系，从而获得无量纲量。

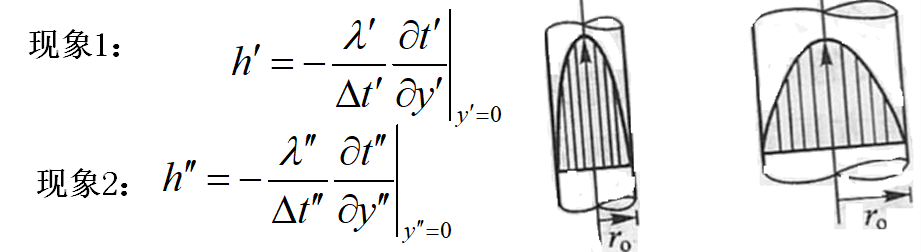
与现象有关的各物理量场应分别相似，即：

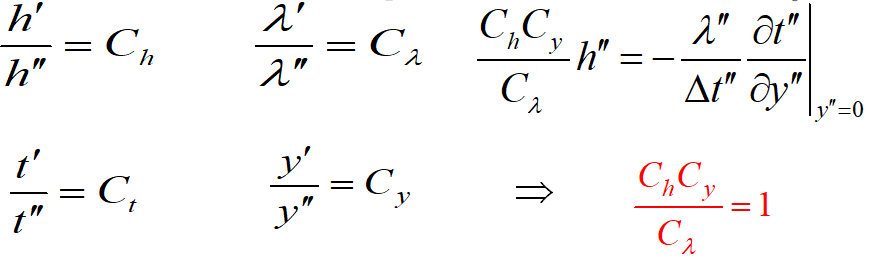
获得无量纲量及其关系：

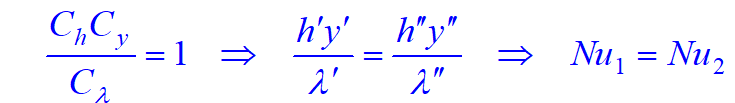
即相似的对流传热现象Nu数相等

类似地：通过动量微分方程可得两流体的运动现象相似，其Re数必定相等；通过能量微分方程可得两热量传递现象相似，其Pe数一定相等。

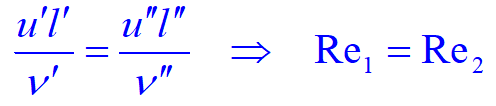
２、量纲分析法

在已知相关物理量的前提下，采用量纲分析获得无量纲量。以圆管内单相强制对流传热为例

(a)确定相关的物理量

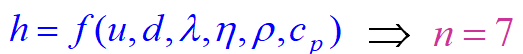
(b)确定基本量纲 r 

上面涉及了4个基本量纲：时间[T]，长度[L]，质量[M]，温度[]  r = 4；所以n – r = 3，即应该有三个无量纲量，因此，我们必须选定4个基本物理量，以与其它量组成三个无量纲量。

(c)组成三个无量纲量 

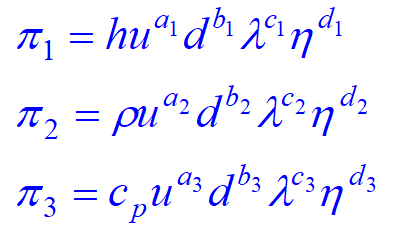
(d)求解待定指数